排序嘉年华———快速排序优化版和非递归思想
文章目录
- 一.单趟排序的优化
-
- 1.“挖坑法”排序
- 2.双指针法
- 二.递归次数的缩减优化
- 三.非递归方式的快排
一.单趟排序的优化
在之前文章中介绍过,霍尔大佬的单趟排序,虽然思想很厉害,但存在许多坑点,比如While循环内条件判定的繁琐,在找大找小很容易不小心写出死循环,所以今天带来两种比较优的单趟方式
1.“挖坑法”排序
挖坑法排序步骤:
1.将默认的left作为key取出进行存储,并并将key的位置设置为hole变量。
2.右边end向左找小,如果比key小,则将值放入坑hole中,并将坑位更新至交换位。
3.左边begin向右找大,如果比key大,则将值放入hole中,并将坑位更新至交换位。
4.以此往复直到二者相遇,将key值放入hole中,单趟完成。
int PartSort1(int* a, int begin, int end)
{ //三数取中
int midi = GetMidi(a, begin, end);
Swap(&a[begin], &a[midi]);
int key = a[begin];
int hole = begin;
while (begin < end)
{
while (begin < end && a[end] >= key)
{
end--;
}
a[hole] = a[end];
hole = end;
while (begin < end && a[begin] <= key)
{
begin++;
}
a[hole] = a[begin];
hole = begin;
}
a[hole] = key;
return hole;
}
三数取中上篇文章讲过,这里不再赘述
将单趟函数提出了,使得结构更加简洁,我们接下来测试一下
void QuickSort(int* a, int begin, int end)
{
if (begin >= end)
return;
//[begin,keyi-1][keyi][keyi+1,end]
int keyi = PartSort1(a, begin, end);
QuickSort(a, begin, keyi - 1);
QuickSort(a, keyi + 1, end);
}
void test1()
{
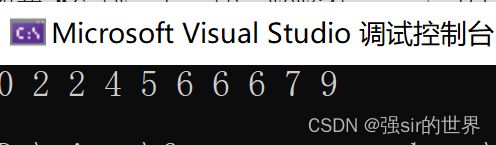
int a[10] = { 9,2,5,6,6,6,7,2,0,4 };
QuickSort(a, 0, 9);
Printarry(a, 10);
}
2.双指针法
前后指针法步骤:
1.创建keyi存储begin]创建指针pre指向begin,创建指针cur指向begin+1。
2.如果cur位置的值比key小,则pre和cur一起向后移动,并交换pre和cur位置的值。
3.如果cur位置的值比key大,则cur向后移动。
4.如此往复直到cur越界后,交换pre和keyi位置的值,将keyi更新为pre。
如图所示
带五角星的是夹在pre与cur之间,全为大于key的值
int PartSort2(int* a, int begin, int end)
{
int midi = GetMidi(a, begin, end);
Swap(&a[midi], &a[begin]);
int keyi = begin;
int prev = begin;
int cur = prev + 1;
while (cur <= end)
{
if (a[cur] < a[keyi] && ++prev != cur)
Swap(&a[prev], &a[cur]);
++cur;
}
Swap(&a[prev], &a[keyi]);
keyi = prev;
return keyi;
}
测试一下仍然没有问题

这种方法在书写上较为简单,是平常较为熟悉的写法
二.递归次数的缩减优化
由于在平常处理数据中可能遇到,数据数量非常庞大,递归次数太多导致栈溢出,所以我们可以从根源出发减少递归次数
思路是如果递归到很深的情况,那一层次数十分庞大,我们可以借助非递归的排序方法辅助进行
缩减递归次数
1.设置阈值:在qsort中这个阈值是7,所以实践中我们可以选择7——10之间。
2.选择排序方法:简短有效且适应性强的排序可以选择插入排序,而且它也是希尔排序的基础。
if (end - begin + 1 <= 7)
{
InsertSort(a + begin, end - begin + 1);
}
加入一步判断,使得排序进程加快
完整代码如下:
void QuickSort1(int* a, int begin, int end)
{
if (begin >= end)
return;
//[begin,keyi-1][keyi][keyi+1,end]
if (end - begin + 1 <= 10)
{
Insertsort(a + begin, end - begin + 1);
}
else
{
int keyi = PartSort2(a, begin, end);
QuickSort1(a, begin, keyi - 1);
QuickSort1(a, keyi + 1, end);
}
}
在指定区间内使用插入排序完成
测试一下优化和未优化效率
void TestOP()
{
srand(time(0));
const int N = 1000000;
int* a1 = (int*)malloc(sizeof(int) * N);
int* a2 = (int*)malloc(sizeof(int) * N);
for (int i = 0; i < N; i++)
{
a1[i] = rand();
a2[i] = rand();
}
int begin1 = clock();
QuickSort1(a1, 0, N - 1);
int end1 = clock();
int begin2 = clock();
QuickSort2(a2, 0, N - 1);
int end2 = clock();
printf("QuickSort优化:%d\n", end1 - begin1);
printf("QuickSort原始:%d\n", end2 - begin2);
free(a1);
free(a2);
}
一百万个随机数据,进行测试

这时就会有人问,这优化了个寂寞,但是我们优化的目的是防止栈溢出,减少递归次数,效率其实相差不大,在release版本下差异可以忽略不计

三.非递归方式的快排
非递归快排最重要的两点是循环,栈。
1.创建一个栈,用于保存待排序子数组的起始索引和结束索引。
2.将整个数组的起始索引和结束索引入栈。
3.循环执行以下步骤,直到栈为空:
出栈得到当前子数组的起始索引和结束索引。
对当前子数组进行分区操作,找到基准值的位置。
如果基准值左边的子数组元素个数大于1,将左边子数组的起始索引和结束索引入栈。
如果基准值右边的子数组元素个数大于1,将右边子数组的起始索引和结束索引入栈。
通过以上步骤,可以实现非递归方式的快速排序。在每次循环中,栈的出栈操作相当于递归调用快速排序的过程,而栈的入栈操作则相当于保存了待排序子数组的起始索引和结束索引,以便在后续循环中对其进行处理。这种方法避免了递归调用带来的函数调用开销,是一种非常高效的排序算法实现方式

void NRQuickSort(int* a, int begin, int end)
{
ST s;
STInit(&s);
STPush(&s, end);
STPush(&s, begin);
while (!STEmpty(&s))
{
int left = STTop(&s);
STPop(&s);
int right = STTop(&s);
STPop(&s);
int keyi = PartSort2(a, left, right);
// [left, keyi-1] keyi [keyi+1, right]
if (left < keyi - 1)
{
STPush(&s, keyi - 1);
STPush(&s, left);
}
if (keyi + 1 < right)
{
STPush(&s, right);
STPush(&s, keyi + 1);
}
}
STDestroy(&s);
}
在c语言中没有库函数,可以自己手撕一个栈出来,对栈不熟悉的可以参考往期文章
这里注重思想,用结构栈取代递归的栈帧。
感谢收看,记得三联,评论区欢迎讨论。
快排上一节:排序嘉年华———选择排序和快排原始版
