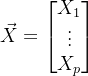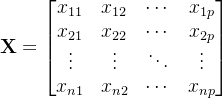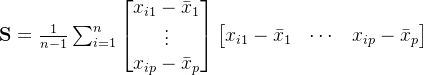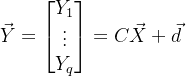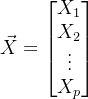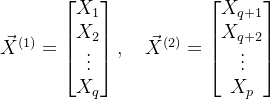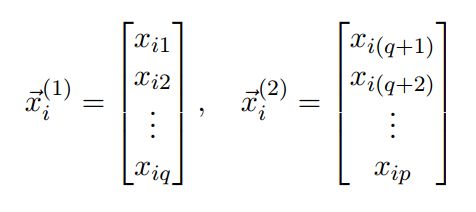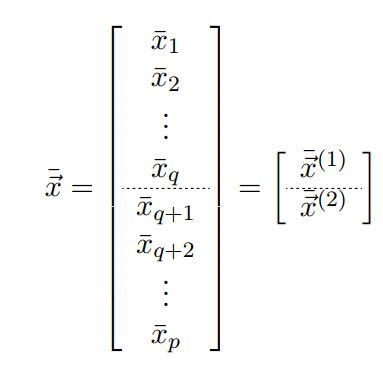详解协方差矩阵，相关矩阵，互协方差矩阵（附完整例题分析）

目录

一. 写在前面

二. 样本向量的均值与协方差

2.1 均值与方差

2.2 向量的均值

2.3 协方差矩阵

三. 协方差矩阵的线性变换

3.1 均值的线性变换

3.2 协方差的线性变换

四. 互协方差矩阵

五. 相关矩阵

六. 例题

---

一. 写在前面

在看MMSE（Minimum Mean Square Error）进行信道估计时，经常看到论文中的这三个表达：

• Correlation Matrix：相关矩阵
• Covariance Matrix：协方差矩阵
• Cross-Covariance Matrix:互协方差矩阵

每次都看的懵懵懂懂，今天尝试用这篇文章，通俗易懂的去解释这三个概率论中的理解。

二. 样本向量的均值与协方差

2.1 均值与方差

我取了n个样本数据，该怎么计算它们的均值？简单，把它们加在一起再除以n就好了：

概率论上把这个叫做无偏样本均值(unbiasd sample mean）。

紧接着利用耳熟能详的方差公式可以计算：

理解：用样本减去平均数再平方，可以衡量样本的波动程度，再除以n-1代表平均波动程度。

注意：是除以n-1，因为当你利用样本均值来代替总体均值时，会损失一个自由度。

2.2 向量的均值

假设现在一个样本不是单一的一个数，而是一个向量。也就是，当你抽取一个样本时，也就相当于抽取了一个p维向量。对应的随机变量也是一个p维向量，如下：

现在，我抽取n个样本向量，每个向量都是p维，也就是抽取了：

注意，我们通常所说的向量如果写成矩阵的格式，一般都代表列向量。

一共n个向量，每个向量包含p个数据，组合在一起不就是矩阵！我们把这个矩阵叫数据矩阵(data matrix），如下：

当你横着看第一行，这就是我们抽取的第一个样本向量，所以下标的第一个数字代表第几次抽取。

当你竖着看第一列，这就是第一个随机变量的n个样本数据，如果只看他这一个的话，这就是一个一维的样本。所以，下标的第二个数字代表第几个随机变量。

所以，这个样本数据矩阵与原始的样本向量关系，如下：

矩阵X第j列代表变量，如果我想要求这个单一变量的样本均值：

简单来讲就是，如果你想要求变量的均值，你就把数据矩阵的第j列进行相加，然后除以n就可以了，很明显这个过程与“2.1”的理解是一模一样的。

以此类推，样本向量的均值计算就很简单了：

如果你对数学推导不感兴趣，请直接看最后的结论：

样本向量的均值也是先相加，再除以n。

2.3 协方差矩阵

取数据矩阵第j列的数据，来代表变量的样本，可以计算对应的方差：

每一个样本都是p维的向量，也就是有p个随机变量，数据的波动程度，是需要考虑不同变量之间的影响，这个时候方差就推广到了协方差。比如，变量与的协方差可以表示为，换个顺序结果肯定相等。变量与的协方差，变量与的协方差，这两个之间是相等的：

协方差的计算跟：第j列和第k列相关，再结合方差的定义。代表第j列的数据波动程度，代表第k列的数据波动程度，由此可得其协方差：

一共有p个变量，任意两个变量进行组合都会出现方差，这种组合的情况一共有种，写成矩阵就是p行p列，这个矩阵就是所谓的协方差矩阵(covariance matrix)：

协方差的计算与理解是本文章的重点。接下来我们尝试带入计算，会用到线性代数的部分知识，还是一样，对概率论不感兴趣的同学，可直接看最后的结论。

协方差矩阵中代表变量1自己跟自己的方差，代表变量1跟变量2之间的方差（更准确叫协方差）。方差的本质无非就是样本减去均值，如此带入协方差矩阵中：

协方差矩阵只是看起来复杂，其本质就是把我们刚才不同位置计算的方差带入而已。

观察到每个地方都有求和，前面都有一个分数，提取出来，化简协方差矩阵：

这是一个对称矩阵，本质就是两个括号相乘，熟悉线性代数的同学知道，这个矩阵可以分解成一个列向量乘以一个行向量，由此可得：

观察第一个列向量：就是第i个样本向量减去样本均值向量

观察第二个行向量：也是第i个样本向量减去样本均值向量，只不过需要转置

小结：

• 协方差矩阵是一个对称矩阵；
• 协方差矩阵的维度与向量维度有关，跟样本向量个数无关；
• 协方差矩阵里元素的值与样本向量和样本向量的均值有关；

具体计算如下：

三. 协方差矩阵的线性变换

如以上讨论中“2.2”,每个样本就是一个p维向量，总共取n个样本向量，放在一起就可以形成一个n行p列的数据矩阵，该矩阵每一行代表一个向量样本，每一列代表一个随机变量的n个取值。

给定向量型随机变量X，我们对其做一些线性变化形成随机变量Y：

其中。首先这是一种线性变换，其次注意随机变量Y的维度也发生了变换。

3.1 均值的线性变换

从样本的角度，思考,x和y之间满足：

其中下标i代表样本个数。样本X取了n次，相当于样本Y也取了n次，所以两者i是一致的。

对n个样本，其样本均值也就比较好计算了：

带入X与Y之间的关系：

换句话说，如果你给出了X的均值，我们可以利用求y的均值，跟以前学习的均值结论一致。

3.2 协方差的线性变换

调用协方差公式计算变量Y的协方差矩阵：

带入X与Y之间的关系：

注意向量d相减被抵消掉了。提取矩阵C，继续化简：

总结变量Y与X之间的协方差矩阵满足：

四. 互协方差矩阵

给定两个向量型随机变量X与Y，它们之间的关系还不明朗，如果需要求它们两之间的互协方差矩阵的话，可以分两步走：

1. 将X与Y合并为1个列向量Z
2. 对向量Z求协方差矩阵

鉴于此思想，我们将从向量分割的角度来解释互协方差矩阵。

给定一个向量型的随机变量：

我们从某处，把该向量分成两个部分（不一定是均分），如下：

可以理解成如下的格式：

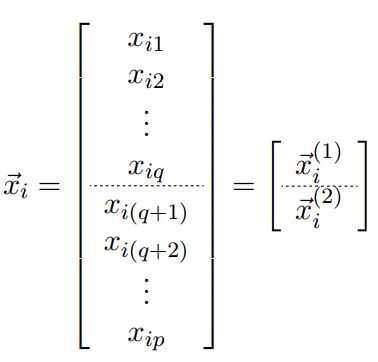
对于每一个取到的向量样本，也可以做这种割分，如下：

两部分样本对应如下：

我们把割分进行到底，样本均值可以直接割分：

向量直接割分，对应两个向量样本，这个没问题。但是协方差的割分是一个矩阵，需要注意，如下：

来理解下协方差矩阵的分割结果：

就是样本的协方差矩阵，q行q列，维度也刚好对应上了。

就是样本的协方差矩阵，(p-q)行(p-q)列，维度也刚好对应上了。

剩下的则是非常有意思的重点。和则可以看成与之间的互-协方差矩阵(cross Covariance Matrix)，观察矩阵元素，不难得到：

五. 相关矩阵

六. 例题

有关五和六，未完待续。