Python高效处理数组类边界情况

图片平滑器问题

图像平滑器 是大小为 3 x 3 的过滤器，用于对图像的每个单元格平滑处理，平滑处理后单元格的值为该单元格的平均灰度。

每个单元格的 平均灰度 定义为：该单元格自身及其周围的 8 个单元格的平均值，结果需向下取整。（即，需要计算蓝色平滑器中 9 个单元格的平均值）。

如果一个单元格周围存在单元格缺失的情况，则计算平均灰度时不考虑缺失的单元格（即，需要计算红色平滑器中 4 个单元格的平均值）。

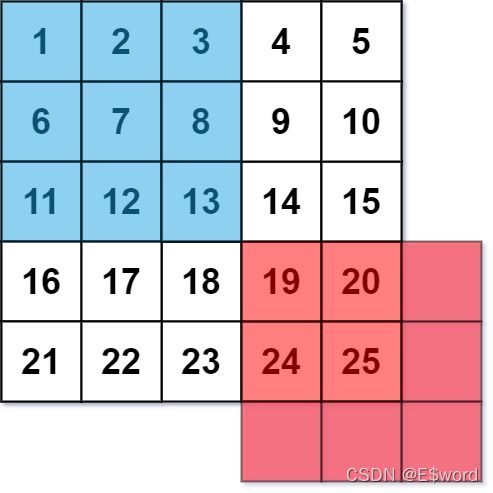
示例：

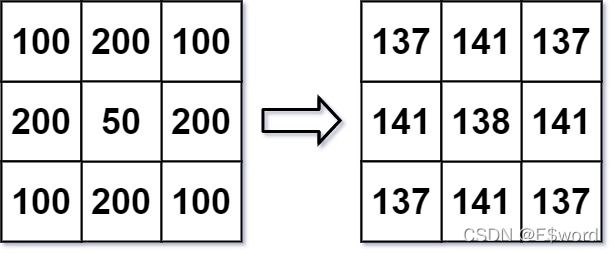
题目ID：661

解法一：直接判断

分别对每种情况进行判断边界
阅读困难

class Solution:
    def imageSmoother(self, img: List[List[int]]) -> List[List[int]]:
        m, n = len(img), len(img[0])
        ans = [[0] * n for _ in range(m)]
        for i in range(m):
            for j in range(n):
                tot, num = 0, 0
                for x in range(i-1, i + 2):
                    for y in range(j - 1, j + 2):
                    	if -1<x<m and -1<y<n:
	                        tot += img[x][y]
	                        num += 1
                ans[i][j] = tot // num
        return ans

解法二：for优化遍历

把边界判断放到for里面
巧用max与min进行筛选

class Solution:
    def imageSmoother(self, img: List[List[int]]) -> List[List[int]]:
        m, n = len(img), len(img[0])
        ans = [[0] * n for _ in range(m)]
        for i in range(m):
            for j in range(n):
                tot, num = 0, 0
                for x in range(max(i - 1, 0), min(i + 2, m)):
                    for y in range(max(j - 1, 0), min(j + 2, n)):
                        tot += img[x][y]
                        num += 1
                ans[i][j] = tot // num
        return ans

解法三：提前构建坐标[荐]

提前存储可

class Solution:
    def imageSmoother(self, img: List[List[int]]) -> List[List[int]]:
        m, n = len(img), len(img[0])
        ans = [[0] * n for _ in range(m)]
        for i in range(m):
            for j in range(n):
                tot, num = 0, 0
                coordinates=[(i+1,j+1),(i,j+1),(i+1,j),(i,j),(i-1,j-1),(i-1,j),(i,j-1),(i+1,j-1),(i-1,j+1)]
                for c in coordinates：
                	x,y=c
                	if -1<x<m and -1<y<n:
                		tot += img[x][y]
                        num += 1
                ans[i][j] = tot // num
        return ans

总结

对于多个需要一次判断边界的坐标，为了使代码易于阅读
可使用上述三种方法。