矩阵微分笔记(1)
目录
- 前言
- 1. 矩阵求导的布局形式
-
- 1.1 矩阵求导的基本单元
-
- f u n c t i o n function function 是一个标量
- f u n c t i o n function function 是一个向量
- f u n c t i o n function function 是一个矩阵
- 1.2 矩阵求导的本质
- 1.3 矩阵求导的布局形式
-
- 1.3.1 向量对标量函数的导数
- 1.3.2 矩阵对标量函数的导数
- 1.3.3 矩阵对矩阵函数的导数
- 1.3.4 分子布局和分母布局的本质
- 参考
前言
前几天学习最优化的时候,发现里面有关于矩阵求导的问题,由于不是很明白当时,就先背了下来。前几天呢也没学别的,因为楼主去拍拖啦~好吧好吧,赶紧学习补回来。
由于我只是一个学统计的(数学边缘人),所写内容可能不是这么严谨,有错误的地方还请大家纠正。但尽管如此,还是得了解一下理论的,我也想当一个调参人- -
首先给定几个前提:
- 为简便起见,仅考虑实数域的矩阵求导,不考虑复数域。
- 如果没有特殊说明,向量 x ⃗ \vec{x} x 默认为列向量的形式,即 x ⃗ = [ x 1 , x 2 , ⋯ , x n ] T \vec{x}=\left [ x_1,x_2,\cdots,x_n\right ]^T x=[x1,x2,⋯,xn]T
1. 矩阵求导的布局形式
1.1 矩阵求导的基本单元
首先我们来看看在矩阵求导中会遇到的一些概念,由于与参考内容的形式不一样,为了明显起见,我用了一种比较容易区分的方式做笔记,希望大家可以理解(什么粗体细体的我真的记不住TAT)
我们会遇到标量、向量、矩阵这三个概念。
先来简单说说标量和向量的区别:如果按照物理上的概念来说的话:标量是数量,没有方向,而向量是有方向的。但在这里有点不同,我们称形式上维度为 1 × 1 1\times 1 1×1 的量为标量,形式上维度为 1 × n 1\times n 1×n 的量为行向量, 形式上维度为 n × 1 n\times 1 n×1 的量为列向量。比如我们记标量为 x x x,向量 x ⃗ = [ x 1 , x 2 , ⋯ , x n ] T \vec{x}=\left [ x_1,x_2,\cdots,x_n\right ]^T x=[x1,x2,⋯,xn]T
然后我们再简单说说矩阵和向量的关系,形式上维度为 n × m n\times m n×m 的量称为矩阵,这里并不要求 n n n 和 m m m 都大于1,这也就说明了其实向量也可以看成一种矩阵。此外,矩阵也可以看成向量,比如我们有矩阵 X = [ x 1 x 2 x 3 x 4 x 5 x 6 x 7 x 8 x 9 ] X=\begin{bmatrix} x_1& x_2 & x_3\\ x_4& x_5& x_6\\ x_7 & x_8&x_9 \end{bmatrix} X= x1x4x7x2x5x8x3x6x9 ,令 α ⃗ i \vec{\alpha}_i αi为矩阵 X X X 的第 i i i 列,则矩阵 X X X 可以写成列向量组 X = [ α ⃗ 1 , α ⃗ 2 , α ⃗ 3 ] X=[\vec{\alpha}_1,\vec{\alpha}_2,\vec{\alpha}_3] X=[α1,α2,α3] 的形式;相应地,如果令 β ⃗ i \vec{\beta}_i βi为矩阵 X X X 的第 i i i 行,则矩阵 X X X 可以写成行向量组 X = [ β ⃗ 1 , β ⃗ 2 , β ⃗ 3 ] T X=[\vec{\beta}_1,\vec{\beta}_2,\vec{\beta}_3]^T X=[β1,β2,β3]T 的形式
下面考虑如下的一个函数
f u n c t i o n ( i n p u t ) function( input) function(input)针对 f u n c t i o n function function 的类型、 i n p u t input input 的类型,我们可以将这个函数 f u n c i o n funcion funcion 分为不同的种类。
f u n c t i o n function function 是一个标量
f u n c t i o n function function是一个实值标量函数,用字母 f f f 表示。根据 i n p u t input input 的类型,我们又可以做如下的划分:
i n p u t input input 是标量
即 f u n t i o n funtion funtion 的输入 i n p u t input input 是标量。用字母 x x x 。比如 f ( x ) = x + 1 f(x)=x+1 f(x)=x+1 x ∈ R x\in\mathbb{R} x∈R, f ( x ) f(x) f(x) 的结果是个取决于 x x x 的值的标量
i n p u t input input 是向量
即 f u n t i o n funtion funtion 的输入 i n p u t input input 是向量。用 x ⃗ \vec{x} x 表示或者粗体小写字母 x \boldsymbol{x} x 表示,如果不做特殊说明,我们默认 x ⃗ \vec{x} x 是 n n n 维列向量,即 x ⃗ = [ x 1 , x 2 , ⋯ , x n ] T \vec{x}=\left [ x_1,x_2,\cdots,x_n\right ]^T x=[x1,x2,⋯,xn]T,比如设 x ⃗ = [ x 1 , x 2 , x 3 ] T \vec{x}=\left[ x_1,x_2, x_3\right]^T x=[x1,x2,x3]T,且有 f ( x ⃗ ) = a 1 x 1 2 + a 2 x 2 2 + a 3 x 3 2 + a 4 x 1 x 2 f(\vec{x})=a_1x_1^2+a_2x_2^2+a_3x_3^2+a_4x_1x_2 f(x)=a1x12+a2x22+a3x32+a4x1x2,其中 x i x_i xi 与 a i a_i ai 均 ∈ R \in\mathbb{R} ∈R
i n p u t input input 是矩阵
即 f u n t i o n funtion funtion 的输入 i n p u t input input 是矩阵。用 X X X 表示,比如这设 X 3 × 2 = ( x i j ) i = 1 , j = 1 3 , 2 \boldsymbol{X}_{3\times2}=(x_{ij})_{i=1,j=1}^{3,2} X3×2=(xij)i=1,j=13,2,且有 f ( X ) = a 1 x 11 2 + a 2 x 12 2 + a 3 x 21 2 + a 4 x 22 2 + a 5 x 31 2 + a 6 x 32 2 \begin{aligned}f(\boldsymbol{X})&=a_1x_{11}^2+a_2x_{12}^2+a_3x_{21}^2+a_4x_{22}^2+a_5x_{31}^2+a_6x_{32}^2\end{aligned} f(X)=a1x112+a2x122+a3x212+a4x222+a5x312+a6x322其中 x i x_i xi 与 a i a_i ai 均 ∈ R \in\mathbb{R} ∈R
f u n c t i o n function function 是一个向量
f u n c t i o n function function 是一个向量时,我们称 f u n c t i o n function function 是一个实向量函数,用 f ⃗ \vec{f} f 或者粗体小写字母 f \boldsymbol{f} f 表示。
含义:实向量函数 f ⃗ \vec{f} f 是由若干个标量函数 f f f 组成的一个向量。
同样地,根据变元 i n p u t input input 的类型可以分类为如下三种:
i n p u t input input 是标量
例如: f ⃗ 3 × 1 ( x ) = [ f 1 ( x ) f 2 ( x ) f 3 ( x ) ] = [ x + 1 2 x + 1 3 x 2 + 1 ] \vec{f}_{3\times1}(x)=\begin{bmatrix}f_1(x)\\f_2(x)\\f_3(x)\end{bmatrix}=\begin{bmatrix}x+1\\2x+1\\3x^2+1\end{bmatrix} f3×1(x)= f1(x)f2(x)f3(x) = x+12x+13x2+1 其中 x ∈ R x\in\mathbb{R} x∈R,即 x x x 是标量
i n p u t input input 是向量
例如:设 x ⃗ = [ x 1 , x 2 , x 3 ] T \vec{x}=[x_1,x_2,x_3]^T x=[x1,x2,x3]T,且有
f ⃗ ( x ⃗ ) = [ f 1 ( x ⃗ ) f 2 ( x ⃗ ) f 3 ( x ⃗ ) ] = [ x 1 + x 2 + x 3 x 1 2 + 2 x 2 + 2 x 3 x 1 x 2 + x 2 + x 3 ] \begin{aligned}\vec{f}(\vec{x})=\begin{bmatrix}f_1(\vec{x})\\f_2(\vec{x})\\f_3(\vec{x})\end{bmatrix}=\begin{bmatrix}x_1+x_2+x_3\\x_1^2+2x_2+2x_3\\x_1x_2+x_2+x_3\end{bmatrix}\end{aligned} f(x)= f1(x)f2(x)f3(x) = x1+x2+x3x12+2x2+2x3x1x2+x2+x3 其中 x ∈ R x\in\mathbb{R} x∈R,向量 x ⃗ ∈ R 3 \vec{x}\in\mathbb{R}^3 x∈R3
i n p u t input input 是矩阵
例如:设 X 3 × 2 = ( x i j ) i = 1 , j = 1 3 , 2 {X}_{3\times2}=(x_{ij})_{i=1,j=1}^{3,2} X3×2=(xij)i=1,j=13,2,且有 f ⃗ 3 × 1 ( X ) = [ f 1 ( X ) f 2 ( X ) f 3 ( X ) ] = [ x 11 + x 12 + x 21 + x 22 + x 31 + x 32 x 11 + x 12 + x 21 + x 22 + x 31 + x 32 + x 11 x 12 2 x 11 + x 12 + x 21 + x 22 + x 31 + x 32 + x 11 x 12 ] \begin{aligned}\left.\vec{f}_{3\times1}(X)=\begin{bmatrix}f_1(X)\\f_2(X)\\f_3(X)\end{bmatrix}=\left[\begin{array}{c}x_{11}+x_{12}+x_{21}+x_{22}+x_{31}+x_{32}\\x_{11}+x_{12}+x_{21}+x_{22}+x_{31}+x_{32}+x_{11}x_{12}\\2x_{11}+x_{12}+x_{21}+x_{22}+x_{31}+x_{32}+x_{11}x_{12}\end{array}\right.\right]\end{aligned} f3×1(X)= f1(X)f2(X)f3(X) = x11+x12+x21+x22+x31+x32x11+x12+x21+x22+x31+x32+x11x122x11+x12+x21+x22+x31+x32+x11x12 其中 x i j x_{ij} xij ∈ R \in\mathbb{R} ∈R
f u n c t i o n function function 是一个矩阵
如果 f u n c t i o n function function 是一个矩阵我们称 f u n c t i o n function function 是一个实矩阵函数,可以用大写字母 F F F 表示。
含义: F F F 是由若干个 f f f 组成的一个矩阵。
同样地,根据变元 i n p u t input input 的类型可以分类为如下三种:
i n p u t input input 是标量
例如:
F 3 × 2 ( x ) = [ f 11 ( x ) f 12 ( x ) f 21 ( x ) f 22 ( x ) f 31 ( x ) f 32 ( x ) ] = [ x + 1 2 x + 2 x 2 + 1 2 x 2 + 1 x 3 + 1 2 x 3 + 1 ] {F}_{3\times2}(x)=\begin{bmatrix}f_{11}(x)&f_{12}(x)\\f_{21}(x)&f_{22}(x)\\f_{31}(x)&f_{32}(x)\end{bmatrix}=\begin{bmatrix}x+1&2x+2\\x^2+1&2x^2+1\\x^3+1&2x^3+1\end{bmatrix} F3×2(x)= f11(x)f21(x)f31(x)f12(x)f22(x)f32(x) = x+1x2+1x3+12x+22x2+12x3+1 其中 f i j f_{ij} fij 都是标量函数, x ∈ R x\in\mathbb{R} x∈R
i n p u t input input 是向量
例如:设 x ⃗ = [ x 1 , x 2 , x 3 ] T \vec{x}=[x_1,x_2,x_3]^T x=[x1,x2,x3]T
F 3 × 2 ( x ⃗ ) = [ f 11 ( x ⃗ ) f 12 ( x ⃗ ) f 21 ( x ⃗ ) f 22 ( x ⃗ ) f 31 ( x ⃗ ) f 32 ( x ⃗ ) ] = [ 2 x 1 + x 2 + x 3 2 x 1 + 2 x 2 + x 3 2 x 1 + 2 x 2 + x 3 x 1 + 2 x 2 + x 3 2 x 1 + x 2 + 2 x 3 x 1 + 2 x 2 + 2 x 3 ] \begin{aligned}{F}_{3\times2}(\vec{x})=\begin{bmatrix}f_{11}(\vec{x})&f_{12}(\vec{x})\\f_{21}(\vec{x})&f_{22}(\vec{x})\\f_{31}(\vec{x})&f_{32}(\vec{x})\end{bmatrix}=\begin{bmatrix}2x_1+x_2+x_3&2x_1+2x_2+x_3\\2x_1+2x_2+x_3&x_1+2x_2+x_3\\2x_1+x_2+2x_3&x_1+2x_2+2x_3\end{bmatrix}\end{aligned} F3×2(x)= f11(x)f21(x)f31(x)f12(x)f22(x)f32(x) = 2x1+x2+x32x1+2x2+x32x1+x2+2x32x1+2x2+x3x1+2x2+x3x1+2x2+2x3 其中 f i j f_{ij} fij 都是 i n p u t input input 为标量的函数, x k ∈ R x_{k}\in\mathbb{R} xk∈R
i n p u t input input 是矩阵
F 3 × 2 ( X ) = [ f 11 ( X ) f 12 ( X ) f 21 ( X ) f 22 ( X ) f 31 ( X ) f 32 ( X ) ] = [ x 11 + x 12 + x 21 + x 22 + x 31 + x 32 2 x 11 + x 12 + x 21 + x 22 + x 31 + x 32 3 x 11 + x 12 + x 21 + x 22 + x 31 + x 32 4 x 11 + x 12 + x 21 + x 22 + x 31 + x 32 5 x 11 + x 12 + x 21 + x 22 + x 31 + x 32 6 x 11 + x 12 + x 21 + x 22 + x 31 + x 32 ] \begin{aligned} F_{3\times2}({X})& =\begin{bmatrix}f_{11}({X})&f_{12}({X})\\f_{21}({X})&f_{22}({X})\\f_{31}({X})&f_{32}({X})\end{bmatrix} \\ &\left.=\left[\begin{array}{ll}x_{11}+x_{12}+x_{21}+x_{22}+x_{31}+x_{32}&2x_{11}+x_{12}+x_{21}+x_{22}+x_{31}+x_{32}\\3x_{11}+x_{12}+x_{21}+x_{22}+x_{31}+x_{32}&4x_{11}+x_{12}+x_{21}+x_{22}+x_{31}+x_{32}\\5x_{11}+x_{12}+x_{21}+x_{22}+x_{31}+x_{32}&6x_{11}+x_{12}+x_{21}+x_{22}+x_{31}+x_{32}\end{array}\right.\right] \end{aligned} F3×2(X)= f11(X)f21(X)f31(X)f12(X)f22(X)f32(X) = x11+x12+x21+x22+x31+x323x11+x12+x21+x22+x31+x325x11+x12+x21+x22+x31+x322x11+x12+x21+x22+x31+x324x11+x12+x21+x22+x31+x326x11+x12+x21+x22+x31+x32 其中 f i j f_{ij} fij 都是 i n p u t input input 为矩阵的函数, x k m ∈ R x_{km}\in\mathbb{R} xkm∈R
实际上,我们仍然可以定义维度更高的矩阵,这个时候的形式就不再局限于以上九种,但再此不做赘述。
1.2 矩阵求导的本质
根据求导的自变量和因变量是标量,向量还是矩阵,我们有9种可能的矩阵求导定义,如下:
| f u n c t i o n / i n p u t function/input function/input | 标量形式的 i n p u t input input | 向量形式的 i n p u t input input | 矩阵形式的 i n p u t input input |
|---|---|---|---|
| 标量形式的 f u n c t i o n function function | f ( x ) f(x) f(x) | f ( x ⃗ ) f(\vec{x}) f(x) | f ( X ) f(X) f(X) |
| 向量形式的 f u n c t i o n function function | f ⃗ ( x ) \vec{f}(x) f(x) | f ⃗ ( x ⃗ ) \vec{f}(\vec{x}) f(x) | f ⃗ ( X ) \vec{f}(X) f(X) |
| 矩阵形式的 f u n c t i o n function function | F ( x ) F(x) F(x) | F ( x ⃗ ) F(\vec{x}) F(x) | F ( X ) F(X) F(X) |
我们在高等数学中,对于如下的多元函数: f ( x 1 , x 2 , x 3 ) = x 1 2 + x 1 x 2 + x 2 x 3 f(x_1,x_2,x_3)=x_1^2+x_1x_2+x_2x_3 f(x1,x2,x3)=x12+x1x2+x2x3我们可以求出 f f f 对 x 1 , x 2 , x 3 x_1,x_2,x_3 x1,x2,x3的偏导数: { ∂ f ∂ x 1 = 2 x 1 + x 2 ∂ f ∂ x 2 = x 1 + x 3 ∂ f ∂ x 3 = x 2 \left.\left\{\begin{aligned}\frac{\partial f}{\partial x_1}&=2x_1+x_2\\\\\frac{\partial f}{\partial x_2}&=x_1+x_3\\\\\frac{\partial f}{\partial x_3}&=x_2\end{aligned}\right.\right. ⎩ ⎨ ⎧∂x1∂f∂x2∂f∂x3∂f=2x1+x2=x1+x3=x2这个时候我们会想:如果我们将每个变元 x 1 , x 2 , x 3 x_1,x_2,x_3 x1,x2,x3看成是一个列向量 x ⃗ = ( x 1 , x 2 , x 3 ) T \vec{x}=(x_1,x_2,x_3)^T x=(x1,x2,x3)T,那么我们就能够将函数 f f f 关于向量 x ⃗ \vec{x} x 的导数表述如下: ∂ f ∂ x ⃗ 3 × 1 = [ ∂ f ∂ x 1 ∂ f ∂ x 2 ∂ f ∂ x 3 ] = [ 2 x 1 + x 2 x 1 + x 3 x 2 ] \frac{\partial f}{\partial \vec{x}_{3\times1}}=\begin{bmatrix} \frac{\partial f}{\partial x_1} \\ \frac{\partial f}{\partial x_2}\\ \frac{\partial f}{\partial x_3} \end{bmatrix}\left.=\left[\begin{array}{c}2x_1+x_2\\x_1+x_3\\x_2\end{array}\right.\right] ∂x3×1∂f= ∂x1∂f∂x2∂f∂x3∂f = 2x1+x2x1+x3x2
也就是说,上述过程便是一个标量函数对向量求导的例子。实际上,矩阵求导本质是 f u n c t i o n function function 中的每个标量函数 f f f 分别对变元中的每个标量元素逐个求偏导,只不过将结果写成了向量或者矩阵形式而已。
上述例子的向量是列向量,那么自然就会有疑问,我们能不能用标量函数对行向量求导数呢?答案当然是肯定的,其形式如下所示: ∂ f ( x ) ∂ x ⃗ 3 × 1 T = [ ∂ f ∂ x 1 , ∂ f ∂ x 2 , ∂ f ∂ x 3 ] = [ 2 x 1 + x 2 , x 1 + x 3 , x 2 ] \frac{\partial f(\boldsymbol{x})}{\partial\vec{x}_{3\times1}^T}=\left[\frac{\partial f}{\partial x_1},\frac{\partial f}{\partial x_2},\frac{\partial f}{\partial x_3}\right]=[2x_1+x_2,x_1+x_3,x_2] ∂x3×1T∂f(x)=[∂x1∂f,∂x2∂f,∂x3∂f]=[2x1+x2,x1+x3,x2]
如果 f u n c t i o n function function 中有 m m m 个 标量函数 f f f ,变元 i n p u t input input 中有 n n n 个标量元素,那么,每个对变元中的每个元素逐个求偏导后,我们就会产生 m × n m \times n m×n 个结果。我们已经知道,矩阵求导的本质只是把标量求导的结果排列起来,至于是按行排列还是按列排列都是可以的。但是这样也有问题,在我们机器学习算法法优化过程中,如果行向量或者列向量随便写,那么结果就不唯一或者出错,那么如何解决这个问题呢?实际上,我们只需要一开始做一个规定,然后后面的运算都遵守这个规定即可,这便是我们接下来要说的内容
1.3 矩阵求导的布局形式
让我们回顾一下上一张关于不同形式求导数的表格:
| f u n c t i o n / i n p u t function/input function/input | 标量形式的 i n p u t input input | 向量形式的 i n p u t input input | 矩阵形式的 i n p u t input input |
|---|---|---|---|
| 标量形式的 f u n c t i o n function function | f ( x ) f(x) f(x) | f ( x ⃗ ) f(\vec{x}) f(x) | f ( X ) f(X) f(X) |
| 向量形式的 f u n c t i o n function function | f ⃗ ( x ) \vec{f}(x) f(x) | f ⃗ ( x ⃗ ) \vec{f}(\vec{x}) f(x) | f ⃗ ( X ) \vec{f}(X) f(X) |
| 矩阵形式的 f u n c t i o n function function | F ( x ) F(x) F(x) | F ( x ⃗ ) F(\vec{x}) F(x) | F ( X ) F(X) F(X) |
下面以表格中标量对向量或矩阵求导,向量或矩阵对标量求导,以及向量对向量求导这5种情况为例来看看矩阵求导的布局形式到底是个什么东西
这里先给出一个结论,矩阵求导有两种布局,分别是分子布局(numerator layout)和分母布局(denominator layout)。首先我们先粗略的给出两种布局的解释,并以该解释为基础,再不加证明地给出各形式求导的结果以比较不同布局形式的特点
分子布局:就是分子是列向量形式,分母是行向量形式,如前面提到的例子: ∂ f ∂ x ⃗ 3 × 1 = [ ∂ f ∂ x 1 ∂ f ∂ x 2 ∂ f ∂ x 3 ] = [ 2 x 1 + x 2 x 1 + x 3 x 2 ] \frac{\partial f}{\partial \vec{x}_{3\times1}}=\begin{bmatrix} \frac{\partial f}{\partial x_1} \\ \frac{\partial f}{\partial x_2}\\ \frac{\partial f}{\partial x_3} \end{bmatrix}\left.=\left[\begin{array}{c}2x_1+x_2\\x_1+x_3\\x_2\end{array}\right.\right] ∂x3×1∂f= ∂x1∂f∂x2∂f∂x3∂f = 2x1+x2x1+x3x2 式。如果这里的 f u n t i o n funtion funtion 是实向量函数 f ⃗ 2 × 1 \vec{f}_{2\times1} f2×1的话,结果就是 2 × 3 2\times3 2×3 的矩阵: ∂ f ⃗ 2 × 1 ( x ⃗ ) ∂ x ⃗ 3 × 1 T = [ ∂ f 1 ∂ x 1 ∂ f 1 ∂ x 2 ∂ f 1 ∂ x 3 ∂ f 2 ∂ x 1 ∂ f 2 ∂ x 2 ∂ f 2 ∂ x 3 ] 2 × 3 \begin{align}\frac{\partial\vec {f}_{2\times1}(\vec{x})}{\partial\vec{x}_{3\times1}^T}=\begin{bmatrix}\frac{\partial f_1}{\partial x_1}&\frac{\partial f_1}{\partial x_2}&\frac{\partial f_1}{\partial x_3}\\\frac{\partial f_2}{\partial x_1}&\frac{\partial f_2}{\partial x_2}&\frac{\partial f_2}{\partial x_3}\end{bmatrix}_{2\times3}\end{align} ∂x3×1T∂f2×1(x)=[∂x1∂f1∂x1∂f2∂x2∂f1∂x2∂f2∂x3∂f1∂x3∂f2]2×3相应地我们可以推广到实向量函数 f ⃗ m × 1 \vec{f}_{m\times1} fm×1为 m m m 维列向量,向量 x ⃗ = [ x 1 , x 2 , ⋯ , x n ] T \vec{x}=[x_1,x_2,\cdots,x_n]^T x=[x1,x2,⋯,xn]T为 n n n 维列向量的形式,则结果布局的形式为 m × n m\times n m×n
分母布局,就是分母是列向量形式,分子是行向量形式,如上述例子中的 ∂ f ( x ) ∂ x ⃗ 3 × 1 T = [ ∂ f ∂ x 1 , ∂ f ∂ x 2 , ∂ f ∂ x 3 ] = [ 2 x 1 + x 2 , x 1 + x 3 , x 2 ] \frac{\partial f(\boldsymbol{x})}{\partial\vec{x}_{3\times1}^T}=\left[\frac{\partial f}{\partial x_1},\frac{\partial f}{\partial x_2},\frac{\partial f}{\partial x_3}\right]=[2x_1+x_2,x_1+x_3,x_2] ∂x3×1T∂f(x)=[∂x1∂f,∂x2∂f,∂x3∂f]=[2x1+x2,x1+x3,x2]是实向量函数 f ⃗ 2 × 1 \vec{f}_{2\times1} f2×1的话,结果就是 3 × 2 3\times2 3×2 的矩阵: ∂ f ⃗ 2 × 1 T ( x ⃗ ) ∂ x ⃗ 3 × 1 = [ ∂ f 1 ∂ x 1 ∂ f 2 ∂ x 1 ∂ f 1 ∂ x 2 ∂ f 2 ∂ x 2 ∂ f 1 ∂ x 3 ∂ f 2 ∂ x 3 ] 3 × 2 \begin{align}\frac{\partial\vec{f}_{2\times1}^T(\vec{x})}{\partial\vec{x}_{3\times1}}=\begin{bmatrix}\frac{\partial f_1}{\partial x_1}&\frac{\partial f_2}{\partial x_1}\\\frac{\partial f_1}{\partial x_2}&\frac{\partial f_2}{\partial x_2}\\\frac{\partial f_1}{\partial x_3}&\frac{\partial f_2}{\partial x_3}\end{bmatrix}_{3\times2}\end{align} ∂x3×1∂f2×1T(x)= ∂x1∂f1∂x2∂f1∂x3∂f1∂x1∂f2∂x2∂f2∂x3∂f2 3×2相应地我们可以推广到实向量函数 f ⃗ m × 1 \vec{f}_{m\times1} fm×1为 m m m 维列向量,向量 x ⃗ = [ x 1 , x 2 , ⋯ , x n ] T \vec{x}=[x_1,x_2,\cdots,x_n]^T x=[x1,x2,⋯,xn]T为 n n n 维列向量的形式,则上述结果布局的形式就会变为为 n × m n\times m n×m
1.3.1 向量对标量函数的导数
即向量变元的实值标量函数 f ( x ⃗ ) f(\vec{x}) f(x) , x ⃗ = [ x 1 , x 2 , ⋯ , x n ] T \vec{x}=[x_1,x_2,\cdots,x_n]^T x=[x1,x2,⋯,xn]T
有两种情况:
(1):行向量偏导形式(又称行偏导向量形式)
D x ⃗ f ( x ) = ∂ f ( x ⃗ ) ∂ x ⃗ T = [ ∂ f ∂ x 1 , ∂ f ∂ x 2 , ⋯ , ∂ f ∂ x n ] \begin{align}\operatorname{D}_{\vec{x}}f(\boldsymbol{x})=\frac{\partial f(\vec{x})}{\partial\vec{x}^T}=\left[\frac{\partial f}{\partial x_1},\frac{\partial f}{\partial x_2},\cdots,\frac{\partial f}{\partial x_n}\right]\end{align} Dxf(x)=∂xT∂f(x)=[∂x1∂f,∂x2∂f,⋯,∂xn∂f]
(2):梯度向量形式(又称列向量偏导形式、列偏导向量形式)
∇ x ⃗ f ( x ⃗ ) = ∂ f ( x ⃗ ) ∂ x ⃗ = [ ∂ f ∂ x 1 , ∂ f ∂ x 2 , ⋯ , ∂ f ∂ x n ] T \begin{align}\nabla_{\vec{x}}f(\vec{x})=\frac{\partial f(\vec{x})}{\partial\vec{x}}=\left[\frac{\partial f}{\partial x_1},\frac{\partial f}{\partial x_2},\cdots,\frac{\partial f}{\partial x_n}\right]^T\end{align} ∇xf(x)=∂x∂f(x)=[∂x1∂f,∂x2∂f,⋯,∂xn∂f]T
不难发现,上述的两种形式互为转置
1.3.2 矩阵对标量函数的导数
即矩阵变元的实值标量函数 f ( X ) f(X) f(X) , X m × n = ( x i j ) i = 1 , j = 1 m , n \boldsymbol{X}_{m\times n}=(x_{ij})_{i=1,j=1}^{m,n} Xm×n=(xij)i=1,j=1m,n
为了后续叙述的便利,先介绍一个符号 v e c ( X ) \mathbf{vec}( X) vec(X) ,其作用是将矩阵 X X X 按列堆栈来向量化,向量化后的结果是产生了一个新的列向量,其实就是把矩阵 X X X 的第 1 列,第 2 列,直到第 n n n 列取出来,然后按顺序组成一个列向量,即:
v e c ( X ) = [ x 11 , x 21 , ⋯ , x m 1 , x 12 , x 22 , ⋯ , x m 2 , ⋯ , x 1 n , x 2 n , ⋯ , x m n ] T \begin{align} \mathbf{vec}(\boldsymbol{X})=[x_{11},x_{21},\cdots,x_{m1},x_{12},x_{22},\cdots,x_{m2},\cdots,x_{1n},x_{2n},\cdots,x_{mn}]^T\end{align} vec(X)=[x11,x21,⋯,xm1,x12,x22,⋯,xm2,⋯,x1n,x2n,⋯,xmn]T
(1):行向量偏导形式(又称行偏导向量形式)
即先把矩阵变元 X X X 按 v e c ( X ) \mathbf{vec}(X) vec(X)向量化,转换成向量变元,再对该向量变元使用公式(3)可以得到 D v e c X f ( X ) = ∂ f ( X ) ∂ v e c T ( X ) = [ ∂ f ∂ x 11 , ∂ f ∂ x 21 , ⋯ , ∂ f ∂ x m 1 , ∂ f ∂ x 12 , ∂ f ∂ x 22 , ⋯ , ∂ f ∂ x m 2 , ⋯ , ∂ f ∂ x 1 n , ∂ f ∂ x 2 n , ⋯ , ∂ f ∂ x m n ] \begin{align} \mathrm{D}_{\mathbf{vec}{X}}f({X})& =\frac{\partial f({X})}{\partial\mathbf{vec}^T({X})} \\ \notag &=\left[\frac{\partial f}{\partial x_{11}},\frac{\partial f}{\partial x_{21}},\cdots,\frac{\partial f}{\partial x_{m1}},\frac{\partial f}{\partial x_{12}},\frac{\partial f}{\partial x_{22}},\cdots,\frac{\partial f}{\partial x_{m2}},\cdots,\frac{\partial f}{\partial x_{1n}},\frac{\partial f}{\partial x_{2n}},\cdots,\frac{\partial f}{\partial x_{mn}}\right] \end{align} DvecXf(X)=∂vecT(X)∂f(X)=[∂x11∂f,∂x21∂f,⋯,∂xm1∂f,∂x12∂f,∂x22∂f,⋯,∂xm2∂f,⋯,∂x1n∂f,∂x2n∂f,⋯,∂xmn∂f]
(2): J a c o b i a n \mathbf{Jacobian} Jacobian 矩阵形式
即先把矩阵变元 X X X 进行转置(分母位置转置),再对转置后的每个位置的元素逐个求偏导,结果布局和转置布局一样。即因为矩阵变元 X X X 是 m × n m\times n m×n 维的,所以结果布局是 n × m n\times m n×m 维的,即 D X f ( X ) = ∂ f ( X ) ∂ X m × n T = [ ∂ f ∂ x 11 ∂ f ∂ x 21 ⋯ ∂ f ∂ x m 1 ∂ f ∂ x 12 ∂ f ∂ x 22 ⋯ ∂ f ∂ x m 2 ⋮ ⋮ ⋮ ⋮ ∂ f ∂ x 1 n ∂ f ∂ x 2 n ⋯ ∂ f ∂ x m n ] n × m \begin{align} \operatorname{D}_{{X}}f({X})& =\frac{\partial f({X})}{\partial{X}_{m\times n}^T} \\ \notag &=\begin{bmatrix}\frac{\partial f}{\partial x_{11}}&\frac{\partial f}{\partial x_{21}}&\cdots&\frac{\partial f}{\partial x_{m1}}\\\frac{\partial f}{\partial x_{12}}&\frac{\partial f}{\partial x_{22}}&\cdots&\frac{\partial f}{\partial x_{m2}}\\\vdots&\vdots&\vdots&\vdots\\\frac{\partial f}{\partial x_{1n}}&\frac{\partial f}{\partial x_{2n}}&\cdots&\frac{\partial f}{\partial x_{mn}}\end{bmatrix}_{n\times m} \end{align} DXf(X)=∂Xm×nT∂f(X)= ∂x11∂f∂x12∂f⋮∂x1n∂f∂x21∂f∂x22∂f⋮∂x2n∂f⋯⋯⋮⋯∂xm1∂f∂xm2∂f⋮∂xmn∂f n×m
(3):梯度向量形式(又称列向量偏导形式、列偏导向量形式,这个用到的比较多)
即先把矩阵变元 X X X 按 v e c ( X ) \mathbf{vec}(X) vec(X)向量化,转换成向量变元,再对该向量变元使用公式(4),即分子位置转置,可以得到 ∇ v e c X f ( X ) = ∂ f ( X ) ∂ v e c ( X ) = [ ∂ f ∂ x 11 , ∂ f ∂ x 21 , ⋯ , ∂ f ∂ x m 1 , ∂ f ∂ x 12 , ∂ f ∂ x 22 , ⋯ , ∂ f ∂ x m 2 , ⋯ , ∂ f ∂ x 1 n , ∂ f ∂ x 2 n , ⋯ , ∂ f ∂ x m n ] T \begin{align} \nabla_{\mathbf{vec}{X}}f({X})& =\frac{\partial f({X})}{\partial\mathbf{vec}({X})} \\ \notag &=\left[\frac{\partial f}{\partial x_{11}},\frac{\partial f}{\partial x_{21}},\cdots,\frac{\partial f}{\partial x_{m1}},\frac{\partial f}{\partial x_{12}},\frac{\partial f}{\partial x_{22}},\cdots,\frac{\partial f}{\partial x_{m2}},\cdots,\frac{\partial f}{\partial x_{1n}},\frac{\partial f}{\partial x_{2n}},\cdots,\frac{\partial f}{\partial x_{mn}}\right]^T \end{align} ∇vecXf(X)=∂vec(X)∂f(X)=[∂x11∂f,∂x21∂f,⋯,∂xm1∂f,∂x12∂f,∂x22∂f,⋯,∂xm2∂f,⋯,∂x1n∂f,∂x2n∂f,⋯,∂xmn∂f]T即得到的结果是一个梯度向量(列向量)
(4):梯度矩阵形式
直接对矩阵变元 X X X 的每个位置的元素逐个求偏导,结果布局和矩阵变元的维度一样。即矩阵变元 X X X 是 m × n m\times n m×n 维的,所以结果布局也是 m × n m\times n m×n 维的,即 ∇ X f ( X ) = ∂ f ( X ) ∂ X m × n = [ ∂ f ∂ x 11 ∂ f ∂ x 12 ⋯ ∂ f ∂ x 1 m ∂ f ∂ x 21 ∂ f ∂ x 22 ⋯ ∂ f ∂ x 2 m ⋮ ⋮ ⋮ ⋮ ∂ f ∂ x m 1 ∂ f ∂ x m 2 ⋯ ∂ f ∂ x m n ] m × n \begin{align} \nabla_{{X}}f({X})& =\frac{\partial f({X})}{\partial{X}_{m\times n}} \\ \notag &=\begin{bmatrix}\frac{\partial f}{\partial x_{11}}&\frac{\partial f}{\partial x_{12}}&\cdots&\frac{\partial f}{\partial x_{1m}}\\\frac{\partial f}{\partial x_{21}}&\frac{\partial f}{\partial x_{22}}&\cdots&\frac{\partial f}{\partial x_{2m}}\\\vdots&\vdots&\vdots&\vdots\\\frac{\partial f}{\partial x_{m1}}&\frac{\partial f}{\partial x_{m2}}&\cdots&\frac{\partial f}{\partial x_{mn}}\end{bmatrix}_{m\times n} \end{align} ∇Xf(X)=∂Xm×n∂f(X)= ∂x11∂f∂x21∂f⋮∂xm1∂f∂x12∂f∂x22∂f⋮∂xm2∂f⋯⋯⋮⋯∂x1m∂f∂x2m∂f⋮∂xmn∂f m×n
由以上的公式可以发现,对于向量变元的实值标量函数 f ( x ⃗ ) f(\vec{x}) f(x) , x ⃗ = [ x 1 , x 2 , ⋯ , x n ] T \vec{x}=[x_1,x_2,\cdots,x_n]^T x=[x1,x2,⋯,xn]T,结果布局本质上有两种形式,一种是 Jacobian 矩阵(行向量) 形式,一种是梯度矩阵(列向量)形式,且这两种形式互为转置。
1.3.3 矩阵对矩阵函数的导数
即矩阵变元的实矩阵函数 F ( X ) , X m × n = ( x i j ) i = 1 , j = 1 m , n , F p × q = ( f i j ) i = 1 , j = 1 p , q F(X)\textit{,}X_{m\times n}=\left(x_{ij}\right)_{i=1,j=1}^{m,n},{F}_{p\times q}=(f_{ij})_{i=1,j=1}^{p,q} F(X),Xm×n=(xij)i=1,j=1m,n,Fp×q=(fij)i=1,j=1p,q
(1): J a c o b i a n \mathbf{Jacobian} Jacobian 矩阵形式
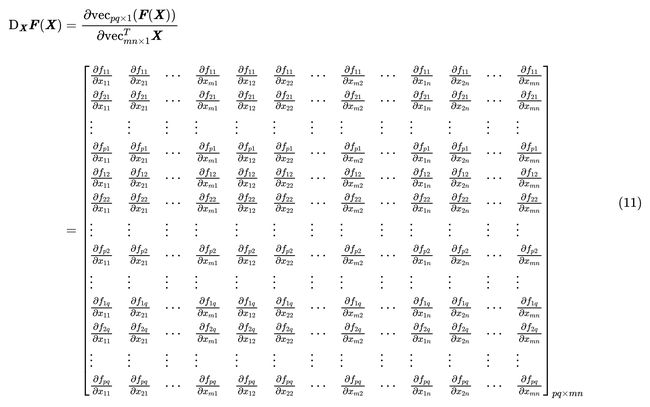
先把矩阵变元 X X X 按 v e c \mathbf{vec} vec 向量化成一个列向量,即转换成向量变元: v e c ( X ) = [ x 11 , x 21 , ⋯ , x m 1 , x 12 , x 22 , ⋯ , x m 2 , ⋯ , x 1 n , x 2 n , ⋯ , x m n ] T \mathbf{vec}({X})=[x_{11},x_{21},\cdots,x_{m1},x_{12},x_{22},\cdots,x_{m2},\cdots,x_{1n},x_{2n},\cdots,x_{mn}]^T vec(X)=[x11,x21,⋯,xm1,x12,x22,⋯,xm2,⋯,x1n,x2n,⋯,xmn]T然后再把实矩阵函数 F ( X ) F(X) F(X) 也按 v e c \mathbf{vec} vec 向量化成一个列向量,即转换成实向量函数: v e c ( F ( X ) ) = [ f 11 ( X ) , f 21 ( X ) , ⋯ , f p 1 ( X ) , f 12 ( X ) , f 22 ( X ) , ⋯ , f p 2 ( X ) , ⋯ , f 1 q ( X ) , f 2 q ( X ) , ⋯ , f p q ( X ) ] T \begin{align} & \mathbf{vec}({F}({X})) =[f_{11}(\boldsymbol{X}),f_{21}(\boldsymbol{X}),\cdots,f_{p1}(\boldsymbol{X}),f_{12}(\boldsymbol{X}),f_{22}(\boldsymbol{X}),\cdots,f_{p2}(\boldsymbol{X}),\cdots,f_{1q}(\boldsymbol{X}),f_{2q}(\boldsymbol{X}), \cdots,f_{pq}(\boldsymbol{X})]^T \end{align} vec(F(X))=[f11(X),f21(X),⋯,fp1(X),f12(X),f22(X),⋯,fp2(X),⋯,f1q(X),f2q(X),⋯,fpq(X)]T那么我们可以利用前面的公式(1)来实现向量对向量函数的导数的行向量偏导形式,由于分子是维数是 p q × 1 pq\times 1 pq×1 的列向量,分母的维度是 1 × m n 1 \times mn 1×mn 的行向量,所以结果布局的维数是 p q × m n pq \times mn pq×mn 维的,具体公式如下表示:(由于这里的Latex显示不了,于是就用图片替代了)
(2):梯度矩阵形式
先把矩阵变元 X X X 按 v e c \mathbf{vec} vec 向量化成一个列向量,即转换成向量变元: v e c ( X ) = [ x 11 , x 21 , ⋯ , x m 1 , x 12 , x 22 , ⋯ , x m 2 , ⋯ , x 1 n , x 2 n , ⋯ , x m n ] T \mathbf{vec}({X})=[x_{11},x_{21},\cdots,x_{m1},x_{12},x_{22},\cdots,x_{m2},\cdots,x_{1n},x_{2n},\cdots,x_{mn}]^T vec(X)=[x11,x21,⋯,xm1,x12,x22,⋯,xm2,⋯,x1n,x2n,⋯,xmn]T然后再把实矩阵函数 F ( X ) F(X) F(X) 也按 v e c \mathbf{vec} vec 向量化成一个列向量,即转换成实向量函数: v e c ( F ( X ) ) = [ f 11 ( X ) , f 21 ( X ) , ⋯ , f p 1 ( X ) , f 12 ( X ) , f 22 ( X ) , ⋯ , f p 2 ( X ) , ⋯ , f 1 q ( X ) , f 2 q ( X ) , ⋯ , f p q ( X ) ] T (12) \begin{aligned} & \mathbf{vec}({F}({X})) =[f_{11}(\boldsymbol{X}),f_{21}(\boldsymbol{X}),\cdots,f_{p1}(\boldsymbol{X}),f_{12}(\boldsymbol{X}),f_{22}(\boldsymbol{X}),\cdots,f_{p2}(\boldsymbol{X}),\cdots,f_{1q}(\boldsymbol{X}),f_{2q}(\boldsymbol{X}), \cdots,f_{pq}(\boldsymbol{X})]^T \\ \tag{12} \end{aligned} vec(F(X))=[f11(X),f21(X),⋯,fp1(X),f12(X),f22(X),⋯,fp2(X),⋯,f1q(X),f2q(X),⋯,fpq(X)]T(12)那么我们可以利用前面的公式(2)来实现向量对向量函数的导数的列向量偏导形式,由于分子是维数是 1 × p q 1\times pq 1×pq 的行向量,分母的维度是 m n × 1 mn \times 1 mn×1 的列向量,所以结果布局的维数是 m n × p q mn \times pq mn×pq 维的,具体公式如下表示:(由于这里的Latex显示不了,于是就用图片替代了)
根据上面的计算可以发现,对于矩阵变元的实值标量函数 f ( X ) f({X}) f(X) , X m × n = ( x i j ) i = 1 , j = 1 m , n {X}_{m\times n}=(x_{ij})_{i=1,j=1}^{m,n} Xm×n=(xij)i=1,j=1m,n,结果布局本质上有四种形式,第一种是 Jacobian 矩阵(行向量) 形式,第二种是梯度矩阵(列向量)形式,第三种是 Jacobian 矩阵(矩阵)形式,第四种是梯度矩阵(矩阵)形式。其中第一种和第二种的结果布局形式互为转置,第三种和第四种的结果布局形式互为转置。
矩阵变元的实向量函数 f ( X ) f(X) f(X) 、向量变元的实向量函数 f ( x ) f(x) f(x) 、向量变元的实矩阵函数 F ( x ⃗ ) F(\vec{x}) F(x)这三个都可以看做是矩阵变元的实矩阵函数 F ( X ) F(X) F(X) ,可使用矩阵对矩阵函数的导数的形式进行计算 (因为向量可以看出一种特殊的矩阵)。
1.3.4 分子布局和分母布局的本质
说到这,其实矩阵求导的结果布局实际上就是分子的转置、向量化,分母的转置、向量化的各种组合。为了方便记忆,我们总结如下:
分子布局的本质:分子是标量、列向量、矩阵向量化后的列向量;分母是标量、列向量转置后的行向量、矩阵的转置矩阵、矩阵向量化后的列向量转置后的行向量。包含公式 (3)式、(6)式、 (7) 式和 (11) 式。一句话就是:分子是列向量,分母是行向量
分母布局的本质:分子是标量、列向量转置后的行向量、矩阵向量化后的列向量转置后的行向量;分母是标量、列向量、矩阵自己、矩阵向量化后的列向量。包含公式(4) 式、(8)式、(9)式和 (12) 式。一句话就是:分子是行向量,分母是列向量
一般情况下,我们都想向量函数 f ⃗ \vec{f} f 和 向量变元 x ⃗ \vec{x} x 都看成列向量,如果二者都不做转置直接求 ∂ f ⃗ ∂ x ⃗ \frac{\partial \vec{f}}{\partial \vec{x}} ∂x∂f,理论上是不够严谨的,为此我们需要对其中一个进行转置,我们可以用一句话来总结:哪个位置不转置就是哪个位置的布局。比如分母不转置,就是分母布局;分子不转置,就是分子布局。
最后用一个表格将这次学习的内容做一个总结:
| 分子/分母 | 标量函数 f f f | (列)向量函数 f ⃗ = [ f 1 , ⋯ , f m ] T \vec{f}=[f_1,\cdots,f_m]^T f=[f1,⋯,fm]T | 矩阵函数 F = ( f i j ) i = 1 , j = 1 p , q F=(f_{ij})_{i=1,j=1}^{p,q} F=(fij)i=1,j=1p,q |
|---|---|---|---|
| 标量 x x x | 高等数学中的导数 | 分子布局: m m m 维列向量 ∂ f ⃗ ∂ x \frac{\partial \vec{f}}{\partial x} ∂x∂f(默认形式) 分母布局: n n n 维行向量 ∂ f ⃗ T ∂ x \frac{\partial \vec{f}^T}{\partial x} ∂x∂fT |
分子布局: p × q p \times q p×q 矩阵 ∂ F ∂ x \frac{\partial F}{\partial x} ∂x∂F (默认形式) 分母布局: q × p q \times p q×p 矩阵 ∂ F T ∂ x \frac{\partial F^T}{\partial x} ∂x∂FT |
| (列)向量 x ⃗ = [ x 1 , ⋯ , x n ] T \vec{x}=[x_1,\cdots,x_n]^T x=[x1,⋯,xn]T | 分子布局: n n n 维行向量 ∂ f ∂ x ⃗ \frac{\partial{f}}{\partial \vec{x}} ∂x∂f 分母布局: n n n 维列向量 ∂ f ⃗ ∂ x ⃗ T \frac{\partial \vec{f}}{\partial \vec{x}^T} ∂xT∂f(默认形式) |
分子布局: m × n m \times n m×n 维雅克比矩阵 ∂ f ⃗ ∂ x T \frac{\partial \vec{f}}{\partial x^T} ∂xT∂f 分母布局: n × m n \times m n×m 维梯度矩阵 ∂ f ⃗ T ∂ x \frac{\partial \vec{f}^T}{\partial x} ∂x∂fT |
|
| 矩阵 X = ( x i j ) i = 1 , j = 1 m , n X=(x_{ij})_{i=1,j=1}^{m,n} X=(xij)i=1,j=1m,n | 分子布局: n × m n \times m n×m 维矩阵 ∂ f ∂ X T \frac{\partial {f}}{\partial X^T} ∂XT∂f 分母布局: n × m n \times m n×m 维梯度矩阵 ∂ f ∂ X \frac{\partial {f}}{\partial X} ∂X∂f (默认形式) |
以上便是矩阵求导的关于布局的内容,下一节将学习具体的矩阵求导法则以及一些典型例子
参考
矩阵求导的本质与分子布局、分母布局的本质(矩阵求导——本质篇)
张贤达《矩阵分析与应用(第二版)》
矩阵的求导