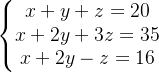利用MATLAB对于符号方程进行求解

在数学计算中，我们经常需要对于方程或者是方程组进行求解，对方程的求解是数学中的一个重要的知识点。在MATLAB中提供了solve函数用于对于符号表达式的求解。solve函数有多种调用方式，包括如下所示：

• solve(equ)：对于等式equ进行求解，所求解的变量是系统默认的。
• solve(equ,var)：对于等式equ进行求解，其中所求解的变量为var。
• solve(eqn1,eqn2,eqn3,...,eqnM,var1,var2,var3,...varN)：对于方程组进行求解，该方程组是由N个变量、M个方程组成的方程组。

下面对于上面几种分别求解和验证。

（1）solve(equ)

solve(equ)是对于等式equ进行求解，所求解的变量是系统默认的。

例如利用solve函数对于下面几个符号表达式进行求解：

MATLAB代码如下所示：

syms x a b
solve((x+2)/3==6)
solve(1/x+2==5)
solve(1/x==1/a+1/b)

运行结果如下所示：

ans =
    16
ans =
    1/3
ans = 
    1/(1/a + 1/b)

通过上面的运行结果可以看出，在符号变量x、a和b中，系统默认使用x作为变量。当符号表达式中有仅有一个变量的时候，MATLAB可以对其值进行准确地求解；当有多变量的时候，系统选定默认变量，也可以对其进行求解。

（2）solve(equ,var)

当函数的调用方式为solve(equ,var)，此时MATLAB对于方程equ的特定变量var进行求解。

例如利用solve对于下面几个符号表达式进行求解：

MATLAB代码如下所示：

syms a b c x y
ans1=solve(a*x+b==2*c,x)
ans2=solve(4*a+b+c==10,a)
ans3=solve(a*x+y==4,a)

运行结果如下所示：

ans1 =
    -(b - 2*c)/a
ans2 =
    5/2 - c/4 - b/4
ans3 =
    -(y - 4)/x

通过上面的运行结果可以看出，当solve函数中指定了特定变量的优先级会高于系统默认的变量的优先级。

（3）solve(eqn1,eqn2,eqn3,...,eqnM,var1,var2,var3,...varN)

当函数的调用方式是solve(eqn1,eqn2,eqn3,...,eqnM,var1,var2,var3,...varN)时，可以对于特定的函数方程组进行求解，其中上面的调用方式中表示有N个变量、M个方程组成的方程组。

例如利用solve对于下面几个符号表达式组进行求解：

MATLAB代码如下所示：

syms x y z a
[x1,y1]=solve(2*x+y==9,x-y==3,x,y)
[x2,y2,z2]=solve(x+y+z==20,x+2*y+3*z==45,x+2*y-z==9,x,y,z)
[x3,y3,z3]=solve(x^2+y^2==13,x+y-z==0,x+z==8,x,y,z)
[x4,y4]=solve(x+y==2*a,x-y==a+4,x,y)

运行结果如下所示：

x1 =
    4
y1 =
    1
x2 =
    4
y2 =
    7
z2 =
    9
x3 =
       3
    17/5
y3 =
      2
    6/5
z3 =
       5
    23/5
x4 =
    (3*a)/2 + 2
y4 =
    a/2 - 2

通过上面的公式看出，该种调用方式可对方程组进行求解，并且函数方程式有多个解的时候，MATLAB会将多个解计算出来。