Interpretability Beyond Feature Attribution: Quantitative Testing with Concept Activation Vectors
本篇文章发表于ICML 2018。
文章链接：https://arxiv.org/abs/1711.11279
代码链接：https://github.com/pytorch/captum/blob/master/tutorials/TCAV_Image.ipynb
一、概述
在文章的Abstract部分，作者持有与第一篇文章类似的观点，即当前有很多图像分类器都是在low-level features上进行操作而不是high-level concepts，基于此，本文引入了概念激活向量（Concept Activation Vectors, CAV）；CAV根据human-friendly concepts提供了神经网络高维内部状态；其关键思想在于，将神经网络中的high-dimensional internal state作为辅助而不是阻碍。
作者将展示如何使用方向导数以量化用户定义的概念对分类结果的重要程度。例如，“斑马”的预测对“条纹是否存在”有多敏感。作者描述了“how CAVs may be used to explore hypothese and generate insights for a standard image classification network as well as medical application.”
作者在Introduction部分指出，机器学习领域的可解释性至关重要，一种很自然的可解释方法是根据模型所关注的特征来理解它的预测；例如，对于logistic regression classifiers，coefficient weights通常被解释为每个特征的重要性（这是理所当然的）；而类似的，saliency maps基于first-order derivatives为图像中的每个像素赋予一定的重要性。并且，除了上面所说的大多数模型都关注low-level features而不是人类可以理解的high-lecel concepts的问题之外，模型的中间输出，比如neural activations更是难以理解的。如果用数学语言表示，我们可以将机器学习模型的可解释性即interpretation视为一个“解释函数”：
。其中，
表示由基向量 
张成的向量空间（ 对应于数据，比如input features以及neural activations）；而 
则代表由基向量 
张成的向量空间（ 对应于an unknown set of human-interpretable concepts）。
函数 
如果是linear的，则被称为linear interpretability。 并不需要十分完美，它也许无法解释输入域 的某些方面，而 也无法避免地难以涵盖所有可能的human-interpretable concepts。
“Note the concepts of are not constrained to input features or training data; they can be defined using new, user-provided data. ”
以上这句话指 所包含的concepts并不一定只局限于模型的训练集所能提供的信息，完全可以通过用户自定义的额外的数据集加以定义；仍然以斑马的分类为例，如果我们想知道“条纹”这一concept对“斑马”分类的影响，可以自定义一个数据集，这个数据集中有正、负两个类别：第一个类别是有条纹的图像集合，另一个类别是没有条纹的图像集合。而对“条纹”的具体定义方式则通过本文所提出的概念激活向量CAV所提供，具体而言，训练一个简单的线性分类器以区分包含所定义的concepts的数据与random counterexamples，然后利用the vector orthogonal to the decision boundary即决策边界的法向量以得到CAV。（这一点也比较好理解，决策边界代表了最能将两个类别区分开的边界，而垂直于这个方向的向量就可以代表最能影响分类结果的因素 —— 可能存在其它因素，但有一个最重要的因素 —— 在斑马分类的问题中，根据user-provided dataset，最重要的因素就是“条纹”的存在/不存在。）
TCAV的目标是：
- Accessibility：缺乏机器学习专业知识的用户也可以使用；
- Customization：适用于任何可以想出来的概念，比如“性别”，并且concepts不受限于模型的训练集；
- Plug-in readiness：不需要重新训练或者修改，可以直接使用；
- Global quantification：可以使用单个度量值解释所有类别或数据集，而不仅仅针对单个输入提供解释。
二、方法
- 相关方法（Related works）
在介绍具体方法之前，作者首先回顾了以往的可解释方法。为了达到可解释，领域内通常有两种做法：(i) inherently interpretable models; (ii) post-process the models in way that yields insights.也就是(i) 内在可解释与(ii) 事后可解释。前面介绍的第一篇文章SENN属于第一种，也就是内在的可解释方法；而本篇文章提出的TCAV实际上属于post-hoc方法。作者指出，对于已经拥有高性能模型了的用户而言，第一种方法的代价是十分高昂的，这在第一篇文章中也提到过，有时候post-hoc是一种“不得已而为之”的选择。
而当我们不得不选择post-hoc explanation的时候，面临的问题也绝非容易。其中一个十分关键的挑战是我们所给出的解释是否真的能客观地反映模型复杂的内部运行机制——也就是说，如何确保我们所给的post-hoc explanation一定是对的、一定是忠于原模型的，这个问题在inherent ( or instinct) explanation中就不存在。而解决此问题的方法之一就是使用产生的explanation作为输入，检验模型的输出是否与预想的一致，比如，基于扰动/敏感性分析（perturbation-based /sensitivity analysis-based）的可解释方法。这些方法使用数据点或者特征进行扰动，观察网络如何响应和变化。它们要么选择维持局部一致性（local consistency, i.e., explanation is true for a data point and its neighbors），要么维持全局一致性（global consistency, i.e., explanation is true for most data points in a class）。TCAV属于后者，它根据人类可理解的概念扰动数据点以产生全局解释。然而，局部一致性虽然保证了在数据点及其邻域之间可解释性的一致，但无法保证整个类别的一致性，即，对于属于相同类别的两个数据点，模型可能会生成相互矛盾的解释，这导致用户们对可解释方法的信任度下降；而TCAV是全局的解释，避免了不一致问题的出现。（似乎diss了所有locally explainable的方法？）
Saliency map是一种十分受欢迎的local explanation方法，它会生成一个map以展现原始图像中每个像素的重要性程度（importance of each pixel）。然而saliency maps有一些缺陷：首先saliency map is given conditioned on only one picture，也就是局部可解释性；其次，用户无法自定义saliency map所关注的concepts，即，使用者无法干预（比如，saliency map无法验证“斑马的条纹”对分类的影响；反过来，我们也无法根据saliency map的brightness将模型关注的特征具体化）；最后，一些研究也表明，随机网络和训练后的网络对于同样一张输入图像的saliency map可能是相似的，且普通的图像平移可能导致saliency map产生显著变化，也更容易受到adversial attacks的影响。以上现象都严重降低了此方法的可信度与可靠性。
- 本文方法
不失一般性，假设输入
，具有 
个neurons的前馈层（feedforward layer） 
，such that input inference and its layer activations can be seen as a function 
。
(i) User-defined Concepts as Sets of Examples
方法的第一步就是对感兴趣concepts的定义，可以通过简单地选择表示这个概念的样本集合或者另找一个感兴趣conceptss被标注好的独立外部数据集。这样做的好处上面也提到过，就是概念的定义或获取并不局限于原有的特征、标签或训练集（概念和数据集都是自定义的）；如此一来，不是机器学习领域专家的人就可以通过自己的领域知识去划分数据集以定义感兴趣的concepts（需要做的就只是划分数据集，区分哪些是含有concepts of interest的数据、哪些不含有）。
(ii) Concept Activation Vectors (CAVs)
现在，我们已经有了定义好的感兴趣concepts，接下来就是如何寻找能够代表这些概念的vectors，也就是CAVs。
为了寻找这样一个向量，我们关注layer 的activations，也就是
；易知activations分为两类，一类是examples in the concept set，另一类是random examples；接着寻找可以将两种activations区分开来的超平面（hyperplane），超平面的法线（normal）就被定义为是CAV（图d中的红色箭头）。
现在让我们梳理一下整个流程：(i) 提供一个数据集，这个数据集可以是原有训练集的子集，也可以是外部独立数据集；数据集中有两类数据，一类是代表了感兴趣概念的样本作为正样本，另一类是随机的反例作为负样本；(ii) 训练一个二元线性分类器，用以区分两类数据在layer 产生的activations；(iii) 训练得到这样一个线性分类器后，获得的超平面的法线
（单位向量）就是我们要得到的CAVs。
(iii) Directional Derivatives and Conceptual Sensitivity
作者首先提到了saliency maps计算输出类别对输入像素敏感度的方法：
“Saliency maps use the gradients of logit values with respect to individual input features like pixels, and compute 
， where 
is the logit for a data point 
for class 
and 
is a pixel at position 
in .”
通过使用CAVs和方向导数，可以在网络的第 层沿着CAV方向改变输入，观察输出的响应来判断prediction对concepts的敏感度：
就是计算 
在 
方向的导数，作为敏感度。
Note： 是可变的，也就是说我们可以评估网络的任何层对定义的concepts的响应。
(iv) Testing with CAVs (TCAV)
在上一节最后提到的方向导数是针对具体的某个样本计算的，但是它可以用来评估全局敏感度，即整个数据集对概念的响应，具体的定义方法如下：
TCAV score反映了对所有属于类别 的样本 
在网络的第 层对概念 
的响应程度。具体来说，就是对每一个样本产生的 
进行统计，记录所有大于0的样本数量，除以总样本的数量 
，就得到了最终的TCAV score。Note：在这里只考虑了 的符号，而不关注大小。（可以探索）
(v) Statistical significance testing
TCAV的一个缺陷是可能学习到毫无意义的CAV，因为就算用随机选择的一组图像也会产生一个CAV,使用这种随机概念的测试不太可能有意义。为了防止无意义的CAV/concept对测试产生虚假结果，提出以下统计显著性检验：
“Instead of training a CAV once, against asingle batch of random examples N, we perform multiple training runs, typically 500. A meaningful concept shouldlead to TCAV scores that behave consistently across training runs.”
即，训练500次以获得CAV，并得到TCAV分数，一个有意义的CAV所对应的分数应在训练过程中表现一致（即分数的均值远离0.5）。由此，对TCAV分数进行了双边t检验，如果我们可以拒绝TCAV得分为0.5的原假设，我们就可以认为该CAV对应的概念与类预测相关。此外，还进行了Bonferroni校正。↓
Note：在统计学中，Bonferroni校正是一种抵消多重比较问题的方法。如果在原假设下观测数据的可能性较低，则统计假设检验倾向于拒绝原假设。如果测试了多个假设，观察罕见事件的机会就会增加，因此，错误地拒绝零假设(即犯第一类错误)的可能性也会增加。
三、实验及结果
(i) Sorting Images with CAVs
使用CAV对图片排序，排序方式为图片的中间层输出 与CAV即 的相似度，度量方式使用cosine similarity。
如上图所示（原图挂了，打个码试试...），展示了在条纹图片中与'CEO concept'最相关的图片（竖向条纹，可能是领带）以及最不相关的图片（横向条纹，可能是中年肥胖大叔穿的衣服）。具体来说就是把所有的条纹图像输入到网络中去，得到第 层的表示 ，并将其与CEO concept对应的CAV作余弦相似度。类似地，右边展示的是'Model Women concept'。
(ii) Empirical Deep Dream
最大激活CAV所对应的图像：固定中间层输出为CAV，固定网络权重，反向推理出对应的输入；从左到右分别为“针织的纹理”、“柯基犬”和“西伯利亚哈士奇”。
(iii) Gaining Insights Using TCAV
不同网络的不同层对不同concept的相关性，用以洞察模型的偏差。例如，ping-pong ball与eastasian的相关性很高。
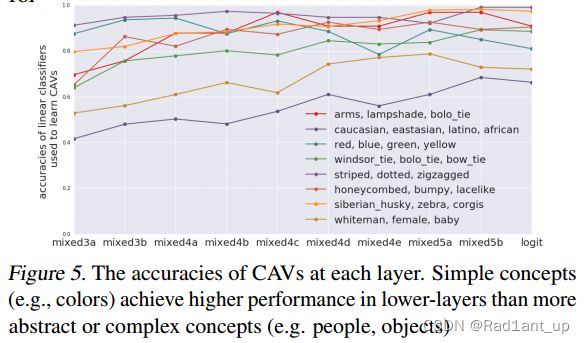
(iv) TCAV for where concepts are learned
对于用于学习CAV的线性分类器而言，在浅层，简单概念比复杂概念的准确度更高，而复杂概念在深层网络表现比浅层网络更好。
这证实了先前的发现，即较低的层作为较低级别的特征检测器(例如，边缘)，而较高的层使用较低级别特征的这些组合来推断较高级别的特征（例如，类别）。
更多结果请参考原论文。