数据结构（一）

本文是在原本数据结构与算法闯关的基础上总结得来，加入了自己的理解和部分习题讲解

原活动链接

邀请码: JL57F5

算法和数据结构

1、什么是算法?

算法，通俗点讲 , 就是一堆小伙伴和一份旅行指南一起前往目的地的过程。每个小伙伴都需要按照指南中的步骤来行动，以达到旅行的目的。同样地，编程中的算法也是一组指令，帮助我们完成特定任务或解决问题.

请注意 : 这里所说的特定问题是多种多样，比如面试经常问的 “将随意排列的数字按从小到大的顺序重新排列”“寻找出发点到目的地的最短路径”，等等一些让人头皮发麻的问题

---

2、什么是数据结构？

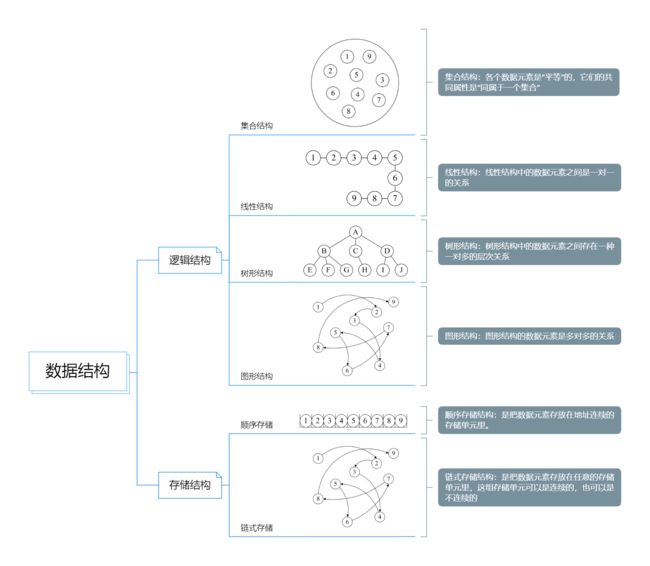
结构，简单的理解就是关系，比如分子结构，就是说组成分子的原子之间的排列方式。严格点说，结构是指各个组成部分相互搭配和排列的方式。在现实世界中，不同数据元素之间不是独立的，而是存在特定的关系，我们将这些关系称为结构。那数据结构是什么？

数据结构：是相互之间存在一种或多种特定关系的数据元素的集合。

按照视点的不同，我们把数据结构分为逻辑结构和存储结构。

大家注意链式存储的定义

如果就是这么简单和有规律，一切就好办了。可实际上，总会有人插队，也会有人要上厕所、有人会放弃排队。如银行、医院等地方，设置了排队系统，也就是每个人去了，先领一个号，等着叫号，叫到时去办理业务或看病。你关注的是前一个号有没有被叫到，叫到了，下一个就轮到了。

因此需要用一个指针存放数据元素的地址，这样通过地址就可以找到相关联数据元素的位置

显然，链式存储就灵活多了，数据存在哪里不重要，只要有一个指针存放了相应的地址就能找到它了。

逻辑结构是面向问题的，而物理结构就是面向计算机的，其基本的目标就是将数据及其逻辑关系存储到计算机的内存中。

常见的数据结构有数组、链表、栈、队列等等。

因此，合适的数据结构不仅可以帮助我们存储和处理不同的数据还能帮助我们我们处理数据的效率和准确性。 知道为什么去面试的时候人家一直问数据结构方面的知识了吧 ？

---

3、算法和数据结构之间的关系

我们通过一个非常著名的公式来总结一下 ：

著名的瑞士科学家N.Wirth教授提出：数据结构+算法＝程序。数据结构是程序的骨架，算法是程序的灵魂。

这句话的含义是，在构建一个程序时，你需要考虑两个重要的方面：数据结构和算法。

1. 数据结构可以被看作是程序的骨架，描述了数据的逻辑组织方式，也是数据在程序中的存储和管理方式。
2. 算法是程序的灵魂，指的是实现某种功能或者解决某个问题的步骤和方法。只有将合适的数据结构与正确的算法结合起来，才能构造出高效、可靠、安全的程序。

比如，在计算机科学中，将搜索的数据存储在二叉树中可以帮助我们快速定位所需的数据。这里，二叉树就是数据结构，而搜索算法就是完成某个功能的具体步骤和方法。如果一旦选择了不恰当的数据结构或算法，程序将无法实现预期的功能，容易出现低效、冗余甚至错误的代码。

因此，可以看出 ， 数据结构和算法是程序开发中必不可少的元素。

1. 数据结构能够帮助我们更好地组织数据，从而让程序更加高效、稳定；
2. 算法使程序能够完成我们所期望的计算和操作。所以，只有当我们掌握了恰当的数据结构和算法，才能够更好地编写高质量的程序。

---

4、时间复杂度

时间复杂度是算法分析中一个很重要的概念，指的是执行当前算法所消耗的时间，通常以大O(order)表示法来表示。

在算法设计和优化中，理解时间复杂度的概念和分析方法非常重要，因为它直接影响算法执行速度和效率，同时也会对算法的空间消耗产生很大的影响。

为了让大家更加好的理解，我们整一个通俗易懂的例子。还是拿做菜来举例子，如果我们要煮水来煮汤，那么加热肯定是需要时间的，而加热的时间取决于我们需要加热的水的量。如果我们要煮一小锅汤（也就是水量少），烧的时间自然会很快。但是如果要煮大锅汤（水量多），那么烧的时间就会增加很多。这个过程就可以理解为时间复杂度，当需要处理的数据规模越大，算法所需要的时间也就越长，时间复杂度也就越高

例如，如果有n个元素需要遍历，算法运算次数随着n的增大而增加，那么我们可以使用线性时间复杂度O(n)来描述它。如果算法具有平方级别的运算次数（这在很多情况下并不理想），我们会把它称为O(n²)时间复杂度。（此篇章我们不会涉及太多， 到时候面试的时候直接记住几个常用的即可）

5、数据结构 : 什么是数组？

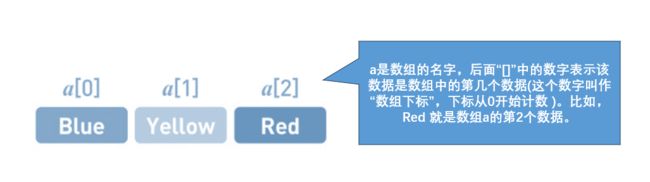
数组是数据呈线性排列的一种数据结构.

数组可以看作是一个盒子，这个盒子里面存放着一些物品。每一个物品都被标上了编号，这些编号从0开始，逐一递增。比如，你可以把一些水果放在盒子里，然后印上编号0、1、2、3…以及它们的名称，这样就形成了一个水果盒子。在这个盒子里，我们可以通过编号来找到指定的物品，比如你希望找到编号为3的物品，它就是盒子里的第四个物品。

在现实生活中，数组的应用非常广泛，比如在超市出售的食品，每个产品都有自己的编号，而且可以随时地在货架上查找到

另外，数组还有一个重要的特性，就是支持随机访问。这意味着我们可以在任何位置访问数组中的元素，而不需要按照特定的顺序逐一遍历。

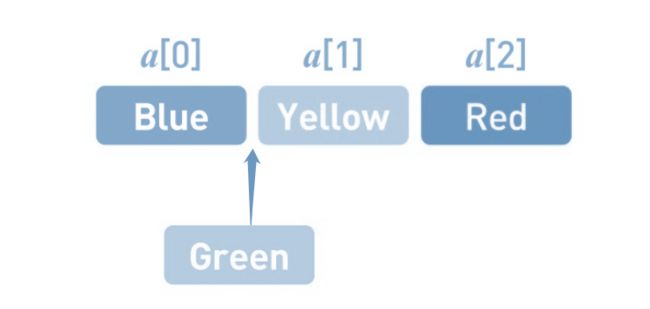
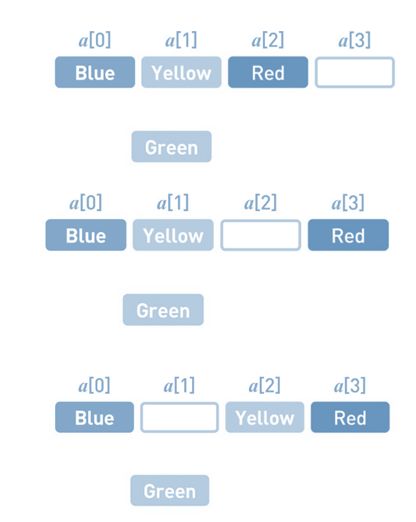
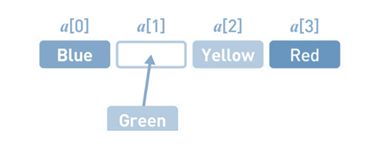
但是，如果想在任意位置上添加或者删除数据 ,就相当于来说会复杂一些 , 比如说现在添加一个Green添加到第2个位置上。

做法 :

首先，在数组的末尾确保需要增加的存储空间。为了给新数据腾出位置，要把已有数据一个个移开。首先把Red往后移。然后把Yellow往后移, 最后在空出来的位置上写入Green。添加数据的操作就完成了。

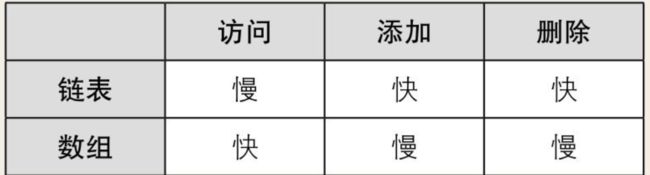
所以 , 虽然数组在访问时非常高效，但是插入和删除元素时会比较棘手，因为它需要对整个数组重新排序。但是，在需要快速访问元素时，数组仍被认为是一种非常有用的数据结构, 也就是数组快速访问高效 , 插入删除低效

关于数组的时间复杂度

对数组操作所花费的运行时间。假设数组中有n个数据，由于访问数据时使用的是随机访问（通过下标可计算出内存地址），所以需要的运行时间仅为恒定的O（1）。

但另一方面，想要向数组中添加新数据时，必须把目标位置后面的数据一个个移开。所以，如果在数组头部添加数据，就需要O（n）的时间

6、数据结构 : 什么是链表？

链表是一种数据呈线性排列的数据结构

链表可以看作是一串火车车厢，车厢里存放了货物。每个车厢都有一个标记，标记着当前车厢的货物，并且还有一个指针，指向下一个车厢。这样，所有的车厢就通过指针构成了一条链，这就是链表。

另外，链表的长度是可以动态增长或者缩短的，因为链表中每个元素通过指针连接，可以通过调整指针来实现链表的插入和删除操作。

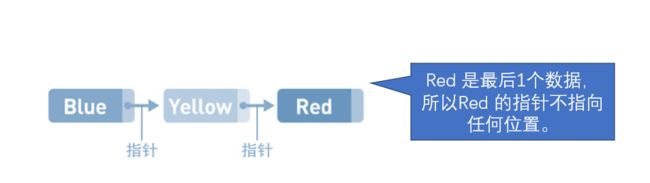
这就是链表的概念图。Blue、Yellow、Red这3个字符串作为数据被存储于链表中。每个数据都有1个“指针”，它指向下一个数据的内存地址。

因为数据都是分散存储的，所以如果想要访问数据，只能从第1个数据开始，顺着指针的指向一一往下访问（这便是顺序访问）。比如，想要找到Red这一数据，就得从Blue开始访问, 之后，还要经过Yellow，我们才能找Red。

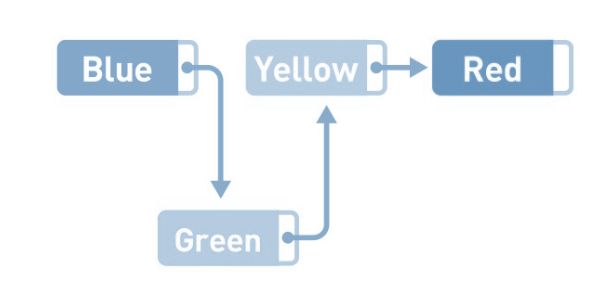
如果想要添加数据，只需要改变添加位置前后的指针指向就可以，非常简单。比如，在Blue和Yellow之间添加Green。将Blue的指针指向的位置变成Green，然后再把Green的指针指向Yellow，数据的添加就大功告成了。

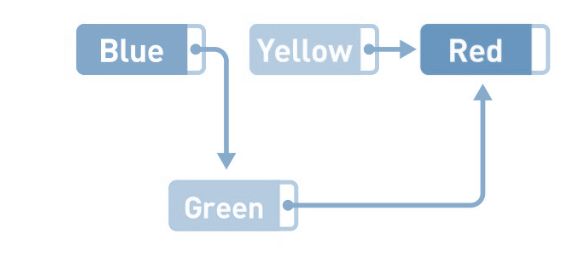
数据的删除也一样，只要改变指针的指向就可以，比如删除Yellow。

这时，只需要把Green指针指向的位置从Yellow变成Red，删除就完成了。虽然Yellow本身还存储在内存中，但是不管从哪里都无法访问这个数据，所以也就没有特意去删除它的必要了。今后需要用到Yellow所在的存储空间时，只要用新数据覆盖掉就可以了。

所以 , 尽管链表的插入和删除操作效率很高，但是访问链表中的元素时效率较低，因为需要按序遍历整个链表寻找目标节点。但在某些场景下，链表仍然是非常有用的数据结构。也就是说 链表插入和删除高效, 快速访问低效

关于链表的时间复杂度

我们把链表中的数据量记成n。访问数据时，我们需要从链表头部开始查找（线性查找），如果目标数据在链表最后的话，需要的时间就是O（n）。

添加数据只需要更改两个指针的指向，所以耗费的时间与n无关。如果已经到达了添加数据的位置，那么添加操作只需花费O（1）的时间。删除数据同样也只需O（1）的时间。

7、链表和数组之间不同点

1. 链表中的元素是通过指针相互连接的，而不是按照顺序排列并分配内存空间的。这意味着对于链表来说，不会像数组一样分配一段连续的内存空间，而是根据需要在内存中随意分配空间。

2. 如果想要进行访问需要进行对链表的遍历才可以

3. 数组中的元素是按照有序编号存储的，这意味着我们可以根据编号直接访问元素，而不需要对整个数组进行遍历。

8、案例讲解 ： 如何通过优化数据结构去解决Python代码运行慢的问题?

在Python中，数据结构的选择对代码的性能有着至关重要的作用。举一个例子，如果你需要存储一组整数，那么Python自带的列表可以选择 ，但是可能是比较低效的选择。

这是因为对于列表来说，它允许存储不同类型的数据，并且在内存中是非连续分配的。这意味着在列表中寻找元素，或者修改列表中的元素可能会涉及到大量的内存分配和复制操作，从而导致代码的性能不佳。

相反，如果你选择使用数组数据结构，就可以避免这种性能问题。数组是内存中连续分配的，只存储一种类型的数据，这使得对于数组的读写操作非常快速。

以下是一个例子：

import numpy as np
import time

# 生成一个包含100万个随机数的python列表
python_list = [i for i in range(1000000)]

# 生成一个包含100万个随机数的numpy数组
numpy_array = np.array(python_list)

# 对Python列表进行加法运算，记录时间
start_time = time.time()
python_list = [num + 1 for num in python_list]
end_time = time.time()
print("python列表加法运算时间:",end_time - start_time)

# 对numpy数组进行加法运算，记录时间
start_time = time.time()
numpy_list = numpy_array + 1
end_time = time.time()
print("numpy数组加法运算时间：",end_time - start_time)

# 对Python列表求平均数，记录时间
start_time = time.time()
avg_python = sum(python_list)/len(python_list)
end_time = time.time()
print("python列表求平均数时间：",end_time - start_time)

# 对numpy数组求平均数，记录时间
start_time = time.time()
avg_numpy = np.mean(numpy_array)
end_time = time.time()
print("numpy列表求平均数时间：",end_time - start_time)

python列表加法运算时间: 0.06781768798828125
numpy数组加法运算时间： 0.0019948482513427734
python列表求平均数时间： 0.01795196533203125
numpy列表求平均数时间： 0.0009970664978027344

假设给定一个字符串，我们要找出其中出现次数最多的字母和出现次数，以下是一种可能的实现方式：

def most_frequent_letter(s):
    # 新建字典freq来存储字符出现的次数
    freq = {}
    # 用 max_count 和 max_char 来记录出现次数 and 字母
    max_count = 0
    max_char = None
    # 遍历字符串 s 中的每个字符，统计出现次数
    for char in s:
        if char in freq:
            freq[char] += 1
        else:
            freq[char] = 1
        # 更新 max_count 和 max_char
        if freq[char] > max_count:
            max_count = freq[char]
            max_char = char
    # 返回出现次数最大的字母和出现次数
    return max_char,max_count

most_frequent_letter("shhsshshshsheeiceubYYYYiwiwwwYYYYY")

('Y', 9)

上面的代码简单地遍历了整个字符串，维护一个字典 freq 来记录每个字母出现的次数，并通过 max_count 和max_char 变量记录出现次数最大的字母和出现次数。

这种实现在小数据集上效果良好，但是在输入字符串较大时可能存在性能瓶颈。对于这种问题，我们可以考虑使用Python 的 Counter 类型，它专为计数问题而设计，可以大大提高代码性能。

改进后的代码如下所示：

# 另外一种解法

from collections import Counter

def most_frequent_letter(s):
    # 使用 Counter 类型计算字符串中每个字符出现的频率
    freq = Counter(s)
    # 返回出现次数最多的字母以及其出现次数，方法 most_common返回所有元素的出现次数，参数表示需要展示的结果数量，1 表示只展示一个结果
    return freq.most_common(1)[0]

most_frequent_letter("shhsshshshsheeiceubYYYYiwiwwwYYYYY")

('Y', 9)

这个版本的代码直接使用 Counter 类型来计算字母出现次数，并通过 most_common 方法返回出现次数最多的字母和出现次数。
这个代码比原先的代码更加简洁和高效。
让你的代码无论是简洁度和性能上都有了很大的提升

闯关题

STEP1：根据要求完成题目
Q1. （单选）数组的元素在内存中是连续存储的，可以通过( )来快速访问元素。
A :下标
B :指针
C : 键
D : 对象

Q2. （单选）链表的元素在内存中不一定是连续存储的，每个元素只保存了下一个元素的地址，所以访问链表中的元素需
A : 从头开始遍历
B : 从尾开始遍历
C : 从最小元素开始遍历
D : 从最大元素开始遍历

Q3. （单选）数组和链表的插入操作时间复杂度分别是多少？
A : O(n)和O(1)
B : O(1)和O(n)
C : O(n)和O(n)
D : O(n²)和O(logn)

Q4.（判断对错)数组的优点是可以快速访问任意位置上的元素，其缺点是插入和删除操作的时间复杂度较高 （T/F)
Q5.（判断对错)链表的优点是插入和删除操作的时间复杂度较低，其缺点是无法快速访问任意位置上的元素 （T/F)

疑问解答：
数组和链表的插入操作时间复杂度有所不同，具体取决于插入位置：

1. 数组的插入操作时间复杂度：

   • 在数组的末尾插入：时间复杂度为 (O(1))，因为不需要移动其他元素。
   • 在数组的开始或中间插入：平均时间复杂度为 (O(n))，因为需要移动插入点后的所有元素来为新元素腾出空间。

2. 链表的插入操作时间复杂度：

   • 在链表的末尾或开始插入：时间复杂度为 (O(1))，如果你有对应的指针（比如尾指针或头指针），因为只需修改几个指针即可。
   • 在链表中间插入：平均时间复杂度为 (O(n))，因为通常需要从头开始遍历链表来找到插入点。但如果已经有了对插入点的直接引用，那么插入操作本身仍然是 (O(1)) 的时间复杂度。

总结来说，数组和链表的插入操作的时间复杂度都与插入位置有关。数组在末尾插入效率较高，而链表在有直接引用的情况下，无论在哪里插入都可以达到 (O(1)) 的时间复杂度。

假设给定一个字符串 ffffsshshshshsdffffffeubYYYYiwiwwwYYYYY。 （友情提示：参考前文写代码去计算）

Q6. 找出该字符串中出现次数最多的字母，赋值给 a6（注意大小写）

Q7. 找出该字符串中出现次数最多的字母的出现次数，赋值给 a7

from collections import Counter

def most_frequent_letter(s):
    # 使用 Counter 类型计算字符串中每个字符出现的频率
    freq = Counter(s)
    # 返回出现次数最多的字母及其出现次数，方法 most_common 返回所有元素的出现次数，参数表示需要展示的结果数量，1 表示只展示一个结果
    return freq.most_common(1)[0]


a6 = most_frequent_letter("ffffsshshshshsdffffffeubYYYYiwiwwwYYYYY")
a6[0]

'f'

a7 = a6[1]
a7

10

#填入你的答案并运行
a1 = 'A'  # 如 a1= 'B'
a2 = 'A'  # 如 a2= 'B'
a3 = 'A'  # 如 a3= 'B'
a4 = 'T'  # 如 a4= 'T'，注意大小写
a5 = 'T'  # 如 a5= 'F'，注意大小写
a6 = 'f'  # 如 a6= 's'，注意大小写
a7 = 10   # 如 a7 = 8

STEP2：将结果保存为 csv 文件
csv 需要有两列，列名：id、answer。其中，id 列为题号，如 q1、q2；answer 列为 STEP1 中各题你计算出来的结果。 这一步的代码你不用做任何修改，直接运行即可。

# 生成 csv 作业答案文件
def save_csv(a1, a2, a3, a4, a5,a6,a7):
    import pandas as pd
    df = pd.DataFrame({"id": ["q1", "q2", "q3", "q4","q5","q6","q7"], "answer": [a1, a2, a3,a4,a5,a6,a7]})
    df.to_csv("answer_ago_1_1.csv", index=None)

save_csv(a1,a2,a3,a4,a5,a6,a7)  # 运行这个cell,生成答案文件；该文件在左侧文件树project工作区下，你可以自行右击下载或者读取查看