消除 TFHE 的限制:WoP-GenPBS
参考文献:
- [CIM19] Carpov S, Izabachène M, Mollimard V. New techniques for multi-value input homomorphic evaluation and applications[C]//Topics in Cryptology–CT-RSA 2019: The Cryptographers’ Track at the RSA Conference 2019, San Francisco, CA, USA, March 4–8, 2019, Proceedings. Springer International Publishing, 2019: 106-126.
- [CGGI20] Chillotti I, Gama N, Georgieva M, et al. TFHE: fast fully homomorphic encryption over the torus[J]. Journal of Cryptology, 2020, 33(1): 34-91.
- [GBA21] Guimarães A, Borin E, Aranha D F. Revisiting the functional bootstrap in TFHE[J]. IACR Transactions on Cryptographic Hardware and Embedded Systems, 2021: 229-253.
- [KPZ21] Kim A, Polyakov Y, Zucca V. Revisiting homomorphic encryption schemes for finite fields[C]//Advances in Cryptology–ASIACRYPT 2021: 27th International Conference on the Theory and Application of Cryptology and Information Security, Singapore, December 6–10, 2021, Proceedings, Part III 27. Springer International Publishing, 2021: 608-639.
- [CLOT21] Chillotti I, Ligier D, Orfila J B, et al. Improved programmable bootstrapping with larger precision and efficient arithmetic circuits for TFHE[C]//Advances in Cryptology–ASIACRYPT 2021: 27th International Conference on the Theory and Application of Cryptology and Information Security, Singapore, December 6–10, 2021, Proceedings, Part III 27. Springer International Publishing, 2021: 670-699.
- [LMP22] Liu Z, Micciancio D, Polyakov Y. Large-precision homomorphic sign evaluation using FHEW/TFHE bootstrap**[C]//International Conference on the Theory and Application of Cryptology and Information Security. Cham: Springer Nature Switzerland, 2022: 130-160.
文章目录
- Building Blocks
-
- GLWE & GLev & GGSW
- LWE-Mult
- Packed-Mult
- Generalized PBS
-
- Module-Switch
- GenPBS
- WoP-PBS
-
- V1
- V2
- Multi-output PBS
- Faster Integer Arithmetic
-
- Boolean
- Modular Power of 2
- Exact Integer
- Faster Circuit Bootstrapping
- Large Precision PBS
-
- Homomorphically Decompose
- Tree-WoP-PBS
[CLOT21] 优化 TFHE 方案,添加了额外的运算和特性,
- FHEW/TFHE 中的 LWE 仅支持线性同态,[CLOT21] 添加了 FV-like 同态乘法,以及 LWE 打包在 RLWE 系数上做批处理
- FHEW/TFHE 的自举是关于 MSB 的,[CLOT21] 使用模切换构造两个小窗口,推广为了 GenPBS
- FHEW/TFHE 只能处理反循环函数,[CLOT21] 通过组合 2、3 个 GenPBS,获得了 WoP-PBS
- [CIM19] 的 Multi-value PBS 采取 ACC 乘以不同的 Test Vector 来同时执行多个 PBS,但这增大了噪声(可能需要提升多项式长度以容错)。[CLOT21] 利用模切换构造出无噪声的小窗口,直接在 LUT 中写入多个函数(本身就需要够长的多项式)做批处理,因此噪声和 GenPBS 是一样的。
- [CLOT21] 利用 GenPBS 的小窗口,对消息的特定区块自举,给出了整数运算的同态进位,从而可以搭建出高精度整数的运算
- [CLOT21] 还提出同态数字分解,这可以和 [GBA21] 的 Tree-PBS 联合使用(它需要将高精度明文用多个 LWE 加密)
在原始 FHEW/TFHE 中,LWE 密文仅支持同态线性运算。LWE 密文的模数需要满足 q ∣ 2 N q \mid 2N q∣2N。为了盲旋转的效率,RLWE 密文的维度 N N N 规模大约是 1024 , 2048 1024,2048 1024,2048,导致 LWE 密文模数也是这个规模(仅 10 10 10 比特),无法支持同态乘法。但是 ACC 的模数 Q ′ ≫ q Q' \gg q Q′≫q 很大(它不必是二的幂,从而支持 NTT 算法),自举结果(模切换 Q ′ → q Q' \to q Q′→q 之前)的噪声可以降低到较低的水平。我们可以让 PBS 输出一个较大的 LWE 密文模数 Q ′ ≥ Q ≫ q Q' \ge Q \gg q Q′≥Q≫q,从而足够支持 LWE 的 FV-like 同态乘法,获得 Level FHE;在自举之前,将 LWE 密文模数从 Q Q Q 切换到满足 q ∣ 2 N q \mid 2N q∣2N 的小模数。
[CLOT21] 统一使用足够大的单个二的幂模数 Q Q Q(因此 ACC 只能用 FFT 算法),在自举之前切换到模数 2 N 2N 2N 上,使用 FV-like 乘法来组合多个 GenPBS 获得 WoP-PBS。他们并且没有给出具体实现和参数选取,[LMP22] 利用 [KPZ21] 的启发式噪声估计,FV-like 乘法导致噪声规模增长 4 N t 4Nt 4Nt(这里 t t t 是明文模数),ACC 的密文模数也应当适应的增加。为了保持安全强度,RLWE 的维度增加到了 4096 4096 4096,这导致 [CLOT21] 的 GenPBS 比通常的 PBS 减速至少一倍。
Building Blocks
GLWE & GLev & GGSW
方便起见,[CLOT21] 描述了三种密文(对称加密)。TFHE 使用 Z q ≅ 1 q Z / Z \mathbb Z_q \cong \frac{1}{q}\mathbb Z/\mathbb Z Zq≅q1Z/Z 来模拟实数环面,模数 q q q 总是二的幂次。
GLWE 密文:私钥 S = ( S 1 , ⋯ , S k ) ∈ R q k S=(S_1,\cdots,S_k) \in R_q^k S=(S1,⋯,Sk)∈Rqk,
G L W E S ( Δ M ) : = ( A 1 , ⋯ , A k , B = ∑ i A i S i + ⌊ Δ M ⌉ + E ) ∈ R q k + 1 GLWE_S(\Delta M) := \left(A_1,\cdots,A_k,B=\sum_i A_iS_i + \lfloor\Delta M\rceil +E\right) \in R_q^{k+1} GLWES(ΔM):=(A1,⋯,Ak,B=i∑AiSi+⌊ΔM⌉+E)∈Rqk+1
其中 A i ∈ R q A_i \in R_q Ai∈Rq 是均匀的, S i , E ∈ R q S_i,E \in R_q Si,E∈Rq 是短噪声。
GLev 密文:数字分解基底 B ∈ N + B \in \mathbb N^+ B∈N+, l = ⌈ log B q ⌉ l=\lceil\log_B q\rceil l=⌈logBq⌉,
G l e v S ( M ) : = { G L W E S ( M ⋅ q B i ) } i = 1 , ⋯ , l ∈ R q ( k + 1 ) × l Glev_S(M) := \left\{GLWE_S\left(M \cdot \frac{q}{B^i}\right)\right\}_{i=1,\cdots,l} \in R_q^{(k+1) \times l} GlevS(M):={GLWES(M⋅Biq)}i=1,⋯,l∈Rq(k+1)×l
数字分解算法满足
⟨ d e c B , l ( a ) , ( q B 1 , ⋯ , q B l ) ⟩ = ⌊ a ⋅ B l q ⌉ ⋅ q B l ∈ R q , ∀ a ∈ R q \left\langle dec^{B,l}(a), (\frac{q}{B^1},\cdots,\frac{q}{B^l}) \right\rangle = \left\lfloor a \cdot \frac{B^l}{q} \right\rceil \cdot \frac{q}{B^l} \in R_q,\,\, \forall a \in R_q ⟨decB,l(a),(B1q,⋯,Blq)⟩=⌊a⋅qBl⌉⋅Blq∈Rq,∀a∈Rq
GGSW 密文:设置 S k + 1 = − 1 S_{k+1}=-1 Sk+1=−1,
G G S W S ( M ) : = { G L e v S ( − S i M ) } i = 1 , ⋯ , k + 1 ∈ R q ( k + 1 ) × l ( k + 1 ) GGSW_S(M) := \left\{GLev_S\left(-S_iM\right)\right\}_{i=1,\cdots,k+1} \in R_q^{(k+1) \times l(k+1)} GGSWS(M):={GLevS(−SiM)}i=1,⋯,k+1∈Rq(k+1)×l(k+1)
TFHE 中的不同部件采取不同的密文类型:
- 加密消息:使用 LWE 密文,秘钥 S = ( S 1 , ⋯ , S k , − 1 ) S=(S_1,\cdots,S_k,-1) S=(S1,⋯,Sk,−1),加密单个整数值 m ∈ Z t m \in \mathbb Z_t m∈Zt
- 秘钥切换:
- PrivKS:秘密的线性态射 f f f,使用 GLev 密文,加密 f ( 0 , ⋯ , S i , ⋯ , 0 ) f(0,\cdots,S_i,\cdots,0) f(0,⋯,Si,⋯,0)
- PubKS:公开的线性态射 f f f,使用 GLev 密文,加密 S i S_i Si
- PackingKS:就是 PubKS,其中的线性态射是一个置换
- 盲旋转:
- ACC:使用 GLWE 密文,加密多项式 P f P_f Pf,它编码了非线性函数 f f f 的 redundant LUT(冗余重复 r r r 次)
- Selector:使用 GGSW 密文,加密 S i S_i Si(GINX 版本的自举,CMux-Based BDD)
当然,对于通常的参数来说,更一般化的 GLWE 计算效率总是不如 RLWE 的。下边的描述中 GLWE、GLev、GGSW 可以总是被视为 k = 1 k=1 k=1 的情况(RLWE、RLev、RGSW),而 LWE 则表示标准 LWE 密文。
LWE-Mult
[CLOT21] 首先回顾了 GLWE 密文的 FV-like 同态乘法(tensor product + relinearization),输入 G L W E ( M 1 Δ 1 ) GLWE(M_1\Delta_1) GLWE(M1Δ1) 和 G L W E ( M 2 Δ 2 ) GLWE(M_2\Delta_2) GLWE(M2Δ2),输出 G L W E ( M 1 M 2 ⋅ Δ ′ ) GLWE(M_1M_2 \cdot\Delta') GLWE(M1M2⋅Δ′),
接着 [CLOT21] 使用 PackingKS 过程,将单个 LWE 密文加密的消息,转化到某个 GLWE 密文的常数项。因此,GLWE 密文之间的 FV-like 同态乘法,其常数项就是原始 LWE 消息的乘积。最后从 GLWE 提取出常数项的 LWE 即可。
在后续的算法中,LWEMult 是关键的部件,被用于组合多个 PBS 的结果,搭建出 WoP-PBS(不需要 Pading 成为半环)
Packed-Mult
为了更高效地计算多个 LWE 密文的同态乘法,[CLOT21] 将它们的消息编码到 GLWE 所加密的多项式不同系数上。
多个独立的乘积:将两组 LWE 密文打包为两个 GLWE 密文,
f 1 ( X ) = ∑ j i ∈ { 0 , 1 , ⋯ , α − 1 } m i ( 1 ) X j i f 2 ( X ) = ∑ j i ∈ { 0 , α , ⋯ , ( α − 1 ) α } m i ( 2 ) X j i \begin{aligned} f_1(X) &= \sum_{j_i \in \{0,1,\cdots,\alpha-1\}} m_i^{(1)}X^{j_i}\\ f_2(X) &= \sum_{j_i \in \{0,\alpha,\cdots,(\alpha-1)\alpha\}} m_i^{(2)}X^{j_i}\\ \end{aligned} f1(X)f2(X)=ji∈{0,1,⋯,α−1}∑mi(1)Xji=ji∈{0,α,⋯,(α−1)α}∑mi(2)Xji
容易看出, f 1 ⋅ f 2 f_1 \cdot f_2 f1⋅f2 的项 X i ⋅ α + i X^{i \cdot \alpha + i} Xi⋅α+i 的系数恰为 m i ( 1 ) m i ( 2 ) m_i^{(1)}m_i^{(2)} mi(1)mi(2),提取它们为 LWE 密文
多个乘积的加和:将两组 LWE 密文打包为两个 GLWE 密文,
f 1 ( X ) = ∑ j i ∈ { 0 , 1 , ⋯ , α − 1 } m i ( 1 ) X j i f 2 ( X ) = ∑ j i ∈ { α − 1 , α − 2 , ⋯ , 0 } m i ( 2 ) X j i \begin{aligned} f_1(X) &= \sum_{j_i \in \{0,1,\cdots,\alpha-1\}} m_i^{(1)}X^{j_i}\\ f_2(X) &= \sum_{j_i \in \{\alpha-1,\alpha-2,\cdots,0\}} m_i^{(2)}X^{j_i}\\ \end{aligned} f1(X)f2(X)=ji∈{0,1,⋯,α−1}∑mi(1)Xji=ji∈{α−1,α−2,⋯,0}∑mi(2)Xji
容易看出, f 1 ⋅ f 2 f_1 \cdot f_2 f1⋅f2 的项 X α − 1 X^{\alpha-1} Xα−1 的系数恰为 ∑ i m i ( 1 ) m i ( 2 ) \sum_i m_i^{(1)}m_i^{(2)} ∑imi(1)mi(2),提取它为 LWE 密文

对于多个独立的平方、多个平方的加和,也有类似的算法。很简单,详见 [CLOT21],略。
注意 [CLOT21] 是将 LWE 的整数采取 Coeff Packing 编码在 GLWE 的多项式上,多项式乘积的系数包含了大量的无用结果,为了不发生回绕多项式的长度 N N N,支持的并行数 α ≤ O ( N ) \alpha \le O(\sqrt{N}) α≤O(N) 是很受限的。而在 BGV/BFV 中是 SIMD 编码的,因此可以支持 N N N 路并行。
Generalized PBS
Module-Switch
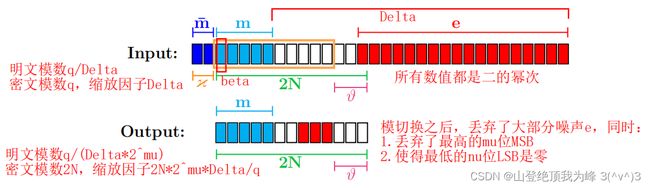
下面的所有参数都是二的幂次(这很关键)。[CLOT21] 使用一种特殊的模切换过程,在 LWE 密文上构造了两个小窗口:
将 L W E ( Δ m ) ∈ Z q k + 1 LWE(\Delta m) \in \mathbb Z_q^{k+1} LWE(Δm)∈Zqk+1 缩放到 L W E ( Δ ′ m ) ∈ Z 2 N k + 1 LWE(\Delta'm) \in \mathbb Z_{2N}^{k+1} LWE(Δ′m)∈Z2Nk+1,
- 缩放前的相位中,长度 μ \mu μ 比特的 MSB(消息的高位)被截掉
- 缩放后的相位中,长度 ν \nu ν 比特的 LSB(噪声的低位)被置零
假设 L W E ( Δ m ) = ( a 1 , ⋯ , a k , a k + 1 = b ) LWE(\Delta m) = (a_1,\cdots,a_k,a_{k+1}=b) LWE(Δm)=(a1,⋯,ak,ak+1=b),密文模数 q q q,明文模数 t = q / Δ t=q/\Delta t=q/Δ。模切换过程为:
a i ′ = [ ⌊ 2 N ⋅ 2 μ − ν q ⋅ a i ⌉ ⋅ 2 ν ] 2 N a_i' = \left[ \left\lfloor \frac{2N \cdot 2^{\mu-\nu}}{q} \cdot a_i \right\rceil \cdot 2^\nu \right]_{2N} ai′=[⌊q2N⋅2μ−ν⋅ai⌉⋅2ν]2N
简记 a i ′ ′ = 2 N ⋅ 2 μ − ν q ⋅ a i a_i'' = \frac{2N \cdot 2^{\mu-\nu}}{q} \cdot a_i ai′′=q2N⋅2μ−ν⋅ai,假设 ⌊ 2 N ⋅ 2 μ − ν q ⋅ a i ⌉ = a i ′ ′ + ϵ i \left\lfloor \frac{2N \cdot 2^{\mu-\nu}}{q} \cdot a_i \right\rceil = a_i''+\epsilon_i ⌊q2N⋅2μ−ν⋅ai⌉=ai′′+ϵi,舍入噪声为 ϵ i ∈ [ − 0.5 , 0.5 ) \epsilon_i \in [-0.5,0.5) ϵi∈[−0.5,0.5),那么 a i ′ = [ ( a i ′ ′ + ϵ i ) ⋅ 2 ν ] 2 N a_i' = [(a_i''+\epsilon_i) \cdot 2^\nu]_{2N} ai′=[(ai′′+ϵi)⋅2ν]2N,它的最低 ν \nu ν 比特是零。
对于 s = ( s 1 , ⋯ , s k , s k + 1 = − 1 ) s=(s_1,\cdots,s_k,s_{k+1}=-1) s=(s1,⋯,sk,sk+1=−1),解密为:
⟨ a ′ , s ⟩ = [ ⟨ ( a ′ ′ + ϵ ) ⋅ 2 ν , s ⟩ ] 2 N = [ 2 N ⋅ 2 μ q ⋅ ⟨ a , s ⟩ + 2 ν ⋅ ⟨ ϵ , s ⟩ ] 2 N = [ 2 N ⋅ 2 μ q ⋅ ( Δ m + e + I q ) + 2 ν ⋅ ⟨ ϵ , s ⟩ ] 2 N = [ ( Δ ⋅ 2 N ⋅ 2 μ q ⋅ m + 2 N ⋅ 2 μ ⋅ I ) + 2 ν ⋅ ( 2 N ⋅ 2 μ − ν q ⋅ e + ⟨ ϵ , s ⟩ ) ] 2 N \begin{aligned} \langle a',s \rangle &= [\langle(a''+\epsilon) \cdot 2^\nu,s\rangle]_{2N}\\ &= \left[ \frac{2N \cdot 2^{\mu}}{q} \cdot \langle a,s \rangle + 2^\nu \cdot \langle \epsilon,s \rangle \right]_{2N}\\ &= \left[ \frac{2N \cdot 2^{\mu}}{q} \cdot (\Delta m+e+Iq) + 2^\nu \cdot \langle \epsilon,s \rangle \right]_{2N}\\ &= \left[ \left(\frac{\Delta \cdot 2N \cdot 2^{\mu}}{q} \cdot m + 2N \cdot 2^{\mu}\cdot I\right) + 2^\nu \cdot \left(\frac{2N \cdot 2^{\mu-\nu}}{q}\cdot e + \langle \epsilon,s \rangle\right) \right]_{2N}\\ \end{aligned} ⟨a′,s⟩=[⟨(a′′+ϵ)⋅2ν,s⟩]2N=[q2N⋅2μ⋅⟨a,s⟩+2ν⋅⟨ϵ,s⟩]2N=[q2N⋅2μ⋅(Δm+e+Iq)+2ν⋅⟨ϵ,s⟩]2N=[(qΔ⋅2N⋅2μ⋅m+2N⋅2μ⋅I)+2ν⋅(q2N⋅2μ−ν⋅e+⟨ϵ,s⟩)]2N
其中的 I I I 是 ⟨ a , s ⟩ ∈ Z \langle a,s\rangle \in \mathbb Z ⟨a,s⟩∈Z 的 q q q-Overflow,可以视为范围有界的随机数。其中的噪声项的最低 ν \nu ν 比特是零。密文模数是 2 N 2N 2N,缩放因子是 Δ ′ = Δ ⋅ 2 N ⋅ 2 μ q \Delta'=\frac{\Delta \cdot 2N \cdot 2^{\mu}}{q} Δ′=qΔ⋅2N⋅2μ,明文模数是 t ′ = q Δ ⋅ 2 μ = t / 2 μ t'=\frac{q}{\Delta \cdot 2^\mu}=t/2^\mu t′=Δ⋅2μq=t/2μ
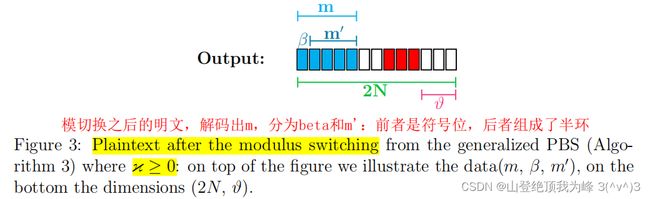
- 当 μ ≥ 0 \mu \ge 0 μ≥0 时 t ′ ≤ t t'\le t t′≤t,相位 [ Δ ′ m + 2 N ⋅ 2 μ ⋅ k + e ′ ] 2 N [\Delta'm+2N \cdot 2^{\mu}\cdot k + e']_{2N} [Δ′m+2N⋅2μ⋅k+e′]2N 的高位存放的是 [ m ] q ′ [m]_{q'} [m]q′,原始 m m m 的最高 μ \mu μ 比特被截掉(上图中的 m ˉ \bar m mˉ)。
- 由于 FHEW/TFHE 的反循环限制,我们将 [ m ] t ′ [m]_{t'} [m]t′ 的 MSB 记为 β = [ [ m ] t ′ ≥ t ′ / 2 ] \beta=[[m]_{t'}\ge t'/2] β=[[m]t′≥t′/2],其余部分记为 m ′ = [ m ] t ′ / 2 m'=[m]_{t'/2} m′=[m]t′/2
- 当 μ < 0 \mu<0 μ<0 时 t ′ > t t'> t t′>t,相位 [ Δ ′ m + 2 N ⋅ 2 μ ⋅ I + e ′ ] 2 N [\Delta'm+2N \cdot 2^{\mu}\cdot I + e']_{2N} [Δ′m+2N⋅2μ⋅I+e′]2N 的高位存放的是 [ m + t ⋅ I ] t ′ [m+t \cdot I]_{t'} [m+t⋅I]t′,原始 m m m 完全保留在它的低位,它的最高 − μ -\mu −μ 比特存放的是 I I I 的最低 − μ -\mu −μ 比特。
- 特别地,当 μ = − 1 \mu=-1 μ=−1 时,最高位 β = [ k ] 2 \beta=[k]_2 β=[k]2 是随机数,其余部分恰好是 m ′ = m m'=m m′=m
GenPBS
利用上述的模切换过程,在执行 TFHE 的盲旋转之前,首先将 R q k + 1 R_q^{k+1} Rqk+1 上的 LWE 密文缩放到 R 2 N k + 1 R_{2N}^{k+1} R2Nk+1 上,它加密的明文是 ( β ∥ m ′ ) (\beta\|m') (β∥m′),其中 m ′ m' m′ 用于查表, β \beta β 用于判定 m ′ m' m′ 位于哪个半环,计算结果为 ( − 1 ) β ⋅ f ( m ′ ) (-1)^\beta \cdot f(m') (−1)β⋅f(m′)
推广的 PBS 过程:
这么做的好处,
- 假如 m m m 的最高 μ \mu μ 比特对于 f f f 的计算没有影响,我们将它截掉,仅把其余部分缩放到在相位高位上,那么即使是较小的多项式长度 N N N, 它编码的 LUT 也有足够的冗余。
- 缩放后相位的噪声最低 ν \nu ν 比特都是零,因此盲旋转的距离总是 2 ν 2^\nu 2ν 倍数,从而相邻的 2 ν 2^\nu 2ν 个系数完全可以编码多个函数的 LUT,从而实现 PBS 的批处理。
WoP-PBS
对于原始的 FHEW/TFHE 自举,它仅能处理反循环的函数。为了计算任意函数,我们将 m m m 的高位添加 Pading Bit(置为零),这使得 ( 0 ∥ m ) (0\|m) (0∥m) 都落在半环内,因此将 f f f 编码到多项式 P f P_f Pf(它编码了半环的 LUT)即可计算出正确的 f ( m ) f(m) f(m)
然而这个技巧使得明文空间扩大了 1 1 1 比特,为了足够的纠错冗余,也许会导致多项式长度 N N N 翻倍(二的幂)。并且 LWE 执行同态线性计算后,总是需要保持 Padding Bit 是零(通过自举来实现)。[CLOT21] 利用上述的 GenPBS 和 LWEMult,实现了不需要 Pading Bit 的自举。
V1
第一个版本的 WoP-PBS,它使用两次 GenPBS:
- 将影响 f f f 的消息 m ′ m' m′ 截下来,同时在 m ′ m' m′ 高位补上一个无用的 β \beta β,
- 根据 β ∥ m ′ \beta\|m' β∥m′,计算出 ( − 1 ) β ⋅ f ( m ′ ) (-1)^\beta \cdot f(m') (−1)β⋅f(m′)
- 根据 β ∥ m ′ \beta\|m' β∥m′,计算出 ( − 1 ) β (-1)^\beta (−1)β
- 使用 LWEMult,计算出 f ( m ′ ) f(m') f(m′)
原始消息 m m m 是直接放在 LWE 的最高比特上的,并没有 Padding Bit。我们用 μ − 1 ≥ 0 \mu-1 \ge 0 μ−1≥0 作为模切换的窗口(作用是在 m ′ m' m′ 高位补 β \beta β),
- 对于 μ ≥ 1 \mu\ge 1 μ≥1,因此 β \beta β 就是 m ′ m' m′ 更高一位的值(无用的)
- 对于 μ = 0 \mu=0 μ=0,因此 β \beta β 就是 I I I 的最低一位的值(随机数)
算法如下:
因为消息 m m m 填满 LWE 相位的最高位,因此 Z t \mathbb Z_{t} Zt 上的同态运算是自然的,并不需要维持 Padding Bit 是零(必须用自举)。因此利用 LWEMult,我们可以将 TFHE 作为一个 Level FHE(同态加法、同态乘法),仅当噪声累积到临界时才执行 WoP-PBS 减少噪声。当然,这需要 ACC 的密文模数增大到支持同态乘法的噪声增长,因此 WoP-PBS 中的 GenPBS 速度更慢。
V2
然而,上述算法事实上是将 m m m 扩大为了 β ∥ m \beta\|m β∥m,因此依旧可能使得多项式长度 N N N 扩大。[CLOT21] 提出另一种方法,类似于 [GBA21] 的 LUT 分块,令 m = β ∥ m ′ m=\beta\|m' m=β∥m′,将任意函数 f f f 分割为两个反循环函数 f 0 ( m ′ ) = f ( 0 ∥ m ′ ) , f 1 ( m ′ ) = f ( 1 ∥ m ′ ) f_0(m')=f(0\|m'), f_1(m')=f(1\|m') f0(m′)=f(0∥m′),f1(m′)=f(1∥m′),最后根据 β = 0 / 1 \beta=0/1 β=0/1 挑选出正确的半环 f β ( m ′ ) = f ( m ) f_\beta(m')=f(m) fβ(m′)=f(m)
算法如下:
分别计算 f 0 , f 1 f_0,f_1 f0,f1 需要 2 2 2 个 GenPBS,提取 β \beta β 也需要 1 1 1 个 GenPBS,共计需要三个 GenPBS。假如采用 V1 会导致长度 N N N 翻倍(两个 O ( 2 N log 2 N ) O(2N\log 2N) O(2Nlog2N) 的 PBS),那么采用 V2 将会更快(三个 O ( N log N ) O(N\log N) O(NlogN) 的 PBS)。另外,采用 [CIM19] 的 Multi-value PBS 或者下面的 Multi-output PBS,这些 GenPBS 可以被批量处理,因此 V2 可能会更具优势。
Multi-output PBS
在 GenPBS 中,LWE 密文执行窗口为 μ , ν \mu,\nu μ,ν 的模切换之后,相位形如 ϕ = Δ ( β ∥ m ′ ) + e ⋅ 2 ν ∈ Z 2 N \phi=\Delta (\beta\|m')+e \cdot 2^\nu \in \mathbb Z_{2N} ϕ=Δ(β∥m′)+e⋅2ν∈Z2N,因此盲旋转的距离 X ϕ X^\phi Xϕ 总是 2 ν 2^\nu 2ν 倍数。换句话说,多项式 P f P_f Pf 中连续的 2 ν 2^\nu 2ν 个系数,只有一个系数被真的用于 LUT 查表。
[CLOT21] 选择将至多 2 ν 2^\nu 2ν 个函数的 LUT 同时写入到 P f P_f Pf 中,简记 p = q Δ ⋅ 2 μ + 1 p=\frac{q}{\Delta \cdot 2^{\mu+1}} p=Δ⋅2μ+1q 是不同取值的个数,冗余 LUT 形如:
在盲旋转(仅一次)的结果中,最低的那 2 ν 2^\nu 2ν 个系数,就编码了 f 1 ( β ∥ m ′ ) , ⋯ , f 2 ν ( β ∥ m ′ ) f_1(\beta\|m'),\cdots,f_{2^\nu}(\beta\|m') f1(β∥m′),⋯,f2ν(β∥m′),可以提取出它们的 LWE 密文。
对比 [CIM19] 的 Multi-value PBS,它需要把 ACC 乘以各个函数的 Test Vector(FHEW-like),这导致了依赖于各个函数的噪声增长。上述的 PBS-manyLUT 直接把这些 LUT 写在了初始的 ACC 内(TFHE-like),噪声和原始的 GenPBS 完全相同。只不过在模切换中的噪声也被乘以 2 ν 2^\nu 2ν,因此它可能需要够大的 N N N
我们可以将 WoP-PBS 和 PBS-manyLUT 组合起来:
- 使用 PBS-manyLUT 加强 WoP-PBS:将其中的 2、3 个 GenPBS 使用单个 PBS-manyLUT 来实现。开销是一个 PBS-manyLUT,效果是一个 WoP-PBS。
- 使用 WoP-PBS 加强 PBS-manyLUT:它本质上就是一个 GenPBS(仅仅是 P f P_f Pf 和 Extract 特殊),容易将它修改为 WoP-PBS 版本。开销是 2、3 个 PBS-manyLUT,效果是一个 WoP-PBS-manyLUT。
Faster Integer Arithmetic
Boolean
在原始的 FHEW/TFHE 中,LWE 密文包含 Padding Bit(总是置为零)。计算逻辑门的时候,拆分为线性部分和非线性部分,
- 执行线性同态,利用 Padding Bit 存储线性部分的结果
- 执行自举,对于 Padding Bit 的内容计算非线性部分,同时降低密文的噪声,以及将 Padding Bit 重新置为零
[CLOT21] 将消息直接加密在 LWE 密文的 MSB 上(没有 Padding Bit),作为 Level FHE 执行,
当噪声累积到临界值,我们执行 PBS 提取出 MSB 的低噪声密文。注意到提取 MSB 就是 Sign 函数,它可以被偏移为一个反循环函数( 0 ↦ − 0.5 , 1 ↦ 0.5 0 \mapsto -0.5,\,\, 1 \mapsto 0.5 0↦−0.5,1↦0.5),因此使用 GenPBS 就足够了。
Modular Power of 2
现在,我们从布尔逻辑 Z 2 \mathbb Z_2 Z2 扩展到整数算术 Z 2 p \mathbb Z_{2^p} Z2p
- 同态加法 A d d 2 p Add_{2^p} Add2p:密文的加法, ( c 1 , c 2 ) ↦ c 1 + c 2 (c_1,c_2) \mapsto c_1+c_2 (c1,c2)↦c1+c2
- 同态乘法 M u l 2 p Mul_{2^p} Mul2p:使用 LWEMult 算法
- 同态取反 O p p 2 p Opp_{2^p} Opp2p:密文的取反, c ↦ − c c \mapsto -c c↦−c
由于 p > 1 p>1 p>1,因此函数 m ↦ m m \mapsto m m↦m 无法写成反循环形式,因此必须使用 WoP-PBS
假设函数 m ↦ m m \mapsto m m↦m 可以写成某个反循环函数, f ( 1 ∥ m ′ ) = − f ( 0 ∥ m ′ ) f(1\|m')=-f(0\|m') f(1∥m′)=−f(0∥m′),希望它经过偏移后计算出 m m m,也就是:对于任意的 m ′ ∈ [ 0 , 2 p − 1 ) m' \in [0,2^{p-1}) m′∈[0,2p−1),都有
m ′ = f ( 0 ∥ m ′ ) + β m ′ + 2 p − 1 = f ( 1 ∥ m ′ ) + β \begin{aligned} m'&= f(0\|m') + \beta\\ m'+2^{p-1}&=f(1\|m')+\beta \end{aligned} m′m′+2p−1=f(0∥m′)+β=f(1∥m′)+β
这推出了 2 m ′ = 2 β − 2 p − 1 , ∀ m ′ ∈ [ 2 p − 1 ] 2m'=2\beta-2^{p-1},\forall m' \in [2^{p-1}] 2m′=2β−2p−1,∀m′∈[2p−1],这是不可能的(除非 p = 1 p=1 p=1)
Exact Integer
为了支持任意精度的整数算术,把整数分为几个精度 2 p 2^p 2p 的小块(Schoolbook Add/Mult),我们需要将给出同态的进位算法。
整数加法的进位,
A d d 2 p M S B ( m 1 , m 2 ) : = ⌊ m 1 + m 2 2 p ⌋ Add_{2^p}^{MSB}(m_1,m_2) := \left\lfloor \frac{m_1+m_2}{2^p} \right\rfloor Add2pMSB(m1,m2):=⌊2pm1+m2⌋
整数乘法的进位,
M u l 2 p M S B ( m 1 , m 2 ) : = ⌊ m 1 ⋅ m 2 2 p ⌋ Mul_{2^p}^{MSB}(m_1,m_2) := \left\lfloor \frac{m_1 \cdot m_2}{2^p} \right\rfloor Mul2pMSB(m1,m2):=⌊2pm1⋅m2⌋
[CLOT21] 的方法是,
- 首先使用 PBS,将 m 1 , m 2 m_1,m_2 m1,m2 的空间放大 p p p 比特,
- 然后我们在空间 Z ( 2 p ) 2 \mathbb Z_{(2^{p})^2} Z(2p)2 上可以正确地模拟 Z \mathbb Z Z 上的算术加法/乘法,它的高 p p p 比特就存储了进位信息
- 利用模切换技术,提取出 m 1 + m 2 , m 1 ⋅ m 2 m_1+m_2, m_1 \cdot m_2 m1+m2,m1⋅m2 的低 p p p 位,进而可以用减法把这些无用数据清零
Faster Circuit Bootstrapping
GGSW 密文是由 k + 1 k+1 k+1 个 GLev 密文组成的,每个 GLev 密文包含 l l l 个 GLWE 密文。确切地说,GGSW 的秘钥为 S = ( S 1 , ⋯ , S k , S k + 1 = − 1 ) S=(S_1,\cdots,S_k,S_{k+1}=-1) S=(S1,⋯,Sk,Sk+1=−1),那么
G G S W S ( m ) = { G L W E S ( − S i ⋅ m ⋅ q B j ) } i , j GGSW_S(m) = \left\{ GLWE_S\left(-S_i \cdot m \cdot \frac{q}{B^j}\right) \right\}_{i,j} GGSWS(m)={GLWES(−Si⋅m⋅Bjq)}i,j
[CGGI17] 给出的电路自举(Circuit Bootstrapping),它将 LWE 密文(加密了数据)转换为 GGSW 密文(作为控制位),从而可以支持和 GLWE 密文的外积(搭建 Level FHE 自动机)。简单来说,
- 输入 L W E K , q ( μ ) , μ ∈ { 0 , 1 } LWE_{K,q}(\mu),\mu \in \{0,1\} LWEK,q(μ),μ∈{0,1},使用 LWE-to-LWE PubKS 将它切换到 L W E K ‾ , 2 N ( μ ) LWE_{\underline K,2N}(\mu) LWEK,2N(μ)
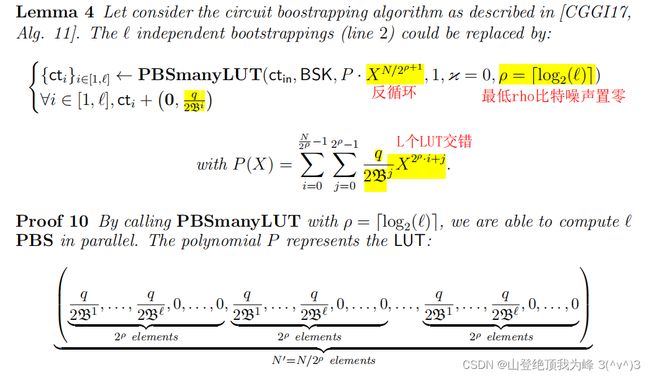
- 使用 l l l 次独立的 LWE-to-LWE PBS(Gate Bootstrapping),构建出 L W E K ‾ , Q ( μ ⋅ Q B j ) , j = 1 , ⋯ , l LWE_{\overline K,Q}\left(\mu \cdot \frac{Q}{B^j}\right),j=1,\cdots,l LWEK,Q(μ⋅BjQ),j=1,⋯,l
- 利用 l ( k + 1 ) l(k+1) l(k+1) 次独立的 LWE-to-GLWE PrivKS,计算出 G L W E K , q ( − K i ⋅ μ ⋅ q B j ) , i = 1 , ⋯ , k + 1 , j = 1 , ⋯ , l GLWE_{K,q}\left(-K_i \cdot \mu \cdot \frac{q}{B^j}\right),i=1,\cdots,k+1,j=1,\cdots,l GLWEK,q(−Ki⋅μ⋅Bjq),i=1,⋯,k+1,j=1,⋯,l
- 这些 GLWE 密文拼成了 G G S W K , q ( μ ) GGSW_{K,q}(\mu) GGSWK,q(μ),可以和其他的 G L W E K , q ( μ ′ ) GLWE_{K,q}(\mu') GLWEK,q(μ′) 做外积
具体算法为:
[CLOT21] 使用 PBS-manyLUT 批处理上述的 l l l 个 PBS,从而减小电路自举的复杂度。各个函数为 f j : μ ↦ μ ⋅ q B j f_j: \mu \mapsto \mu \cdot \frac{q}{B^j} fj:μ↦μ⋅Bjq,分别扭曲为反循环形式,使用 GenPBS 计算它们。
Large Precision PBS
Homomorphically Decompose
利用带窗口的模切换技术,容易将加密了高精度数据 Δ m \Delta m Δm 的单个 LWE 密文,分解为若干个分别加密低精度分块 Δ i m i \Delta_i m_i Δimi 的 LWE 密文,使得满足 Δ m = ∑ i Δ i m i \Delta m = \sum_i \Delta_i m_i Δm=∑iΔimi。注意这里的分解,是将 m i m_i mi 之外的其他分块对应位置置为零, m i m_i mi 依旧被放在原始的位置上(并非存放在最高位)。
我们依次提取出 LSB 部分,然后将它从整体中移除,剩下 MSB 部分。具体算法如下:

在这个分解过程中,每次 WoP-PBS 都仅仅需要支持各个小块的自举,因此多项式长度 N N N 可以是较小的数。最后,将它们加起来,就获得了高精度 LWE 密文的自举。
Tree-WoP-PBS
最后,我们可以将这个分解技术,和 [GBA21] 的 Tree-PBS(它要求输入数据被分块加密)组合使用,从而获得高精度的 WoP-PBS。