算法训练Day32 | LeetCode122. 买卖股票的最佳时机;LeetCode55. 跳跃游戏;LeetCode45. 跳跃游戏II
目录
LeetCode122. 买卖股票的最佳时机
1. 思路
2. 代码实现
3. 复杂度分析
4. 思考与收获
LeetCode55. 跳跃游戏
1. 思路
2. 代码实现
3. 复杂度分析
4. 思考与收获
LeetCode45. 跳跃游戏II
1. 思路
2. 代码实现
3. 复杂度分析
4. 思考与收获
LeetCode122. 买卖股票的最佳时机
LeetCode122. 链接: 122. 买卖股票的最佳时机 II - 力扣(LeetCode)
1. 思路
本题首先要清楚两点:
- 只有一只股票!
- 当前只有买股票或者卖股票的操作
想获得利润至少要两天为一个交易单元,这道题目可能我们只会想,选一个低的买入,在选个高的卖,在选一个低的买入.....循环反复。
如果想到其实最终利润是可以分解的,那么本题就很容易了!
如何分解呢?
假如第0天买入,第3天卖出,那么利润为:prices[3] - prices[0]。相当于(prices[3] - prices[2]) + (prices[2] - prices[1]) + (prices[1] - prices[0]);
此时就是把利润分解为每天为单位的维度,而不是从0天到第3天整体去考虑!
那么根据prices可以得到每天的利润序列:(prices[i] - prices[i - 1]).....(prices[1] - prices[0]);
注意: 一些同学陷入:第一天怎么就没有利润呢,第一天到底算不算的困惑中。第一天当然没有利润,至少要第二天才会有利润,所以利润的序列比股票序列少一天!
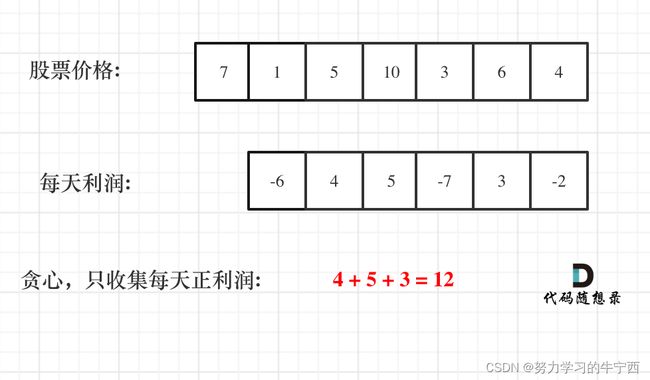
贪心算法:我们需要收集每天的正利润就可以
从图中可以发现,其实我们需要收集每天的正利润就可以,收集正利润的区间,就是股票买卖的区间,而我们只需要关注最终利润,不需要记录区间。
那么只收集正利润就是贪心所贪的地方!
局部最优:收集每天的正利润,全局最优:求得最大利润。
局部最优可以推出全局最优,找不出反例,试一试贪心!
2. 代码实现
在代码实现中,其实并不需要真的创建一个“每天的利润”的数组,只需要在遍历原来的数组上,计算出从第二天开始的利润,并且如果是正数的话就加到result变量中去即可;具体代码实现如下:
# 贪心算法
# time:O(N);space:O(1)
class Solution(object):
def maxProfit(self, prices):
"""
:type prices: List[int]
:rtype: int
"""
result = 0
# 从第二天开始,才有利润
for i in range(1,len(prices)):
# 如果利润小于0,不统计
# 利润大于0,才统计
result += max(0,prices[i]-prices[i-1])
return result
3. 复杂度分析
时间复杂度:O(N);
需要遍历prices数组一次;
空间复杂度:O(1)
只有常数个变量来记录;
4. 思考与收获
-
股票问题其实是一个系列的,属于动态规划的范畴,因为目前在讲解贪心系列,所以股票问题会在之后的动态规划系列中详细讲解;
-
可以看出有时候,贪心往往比动态规划更巧妙,更好用,所以别小看了贪心算法;
-
本题中理解利润拆分是关键点! 不要整块的去看,而是把整体利润拆为每天的利润;一旦想到这里了,很自然就会想到贪心了,即:只收集每天的正利润,最后稳稳的就是最大利润了;
-
(二刷再看)动态规划做法:
class Solution: def maxProfit(self, prices: List[int]) -> int: length = len(prices) dp = [[0] * 2 for _ in range(length)] dp[0][0] = -prices[0] dp[0][1] = 0 for i in range(1, length): dp[i][0] = max(dp[i-1][0], dp[i-1][1] - prices[i]) #注意这里是和121. 买卖股票的最佳时机唯一不同的地方 dp[i][1] = max(dp[i-1][1], dp[i-1][0] + prices[i]) return dp[-1][1]- 时间复杂度:O(n)
- 空间复杂度:O(n)
Reference:代码随想录 (programmercarl.com)
本题学习时间:20分钟。
LeetCode55. 跳跃游戏
LeetCode55. 链接:55. 跳跃游戏 - 力扣(LeetCode)
1. 思路
把问题转换的更简单一点?
刚看到本题一开始可能想:当前位置元素如果是3,我究竟是跳一步呢,还是两步呢,还是三步呢,究竟跳几步才是最优呢?其实跳几步无所谓,关键在于可跳的覆盖范围!
不一定非要明确一次究竟跳几步,每次取最大的跳跃步数,这个就是可以跳跃的覆盖范围。这个范围内,别管是怎么跳的,反正一定可以跳过来。那么这个问题就转化为跳跃覆盖范围究竟可不可以覆盖到终点!
贪心算法怎么贪心呢?
每次移动取最大跳跃步数(得到最大的覆盖范围),每移动一个单位,就更新最大覆盖范围。
贪心算法局部最优解:每次取最大跳跃步数(取最大覆盖范围),整体最优解:最后得到整体最大覆盖范围,看是否能到终点。
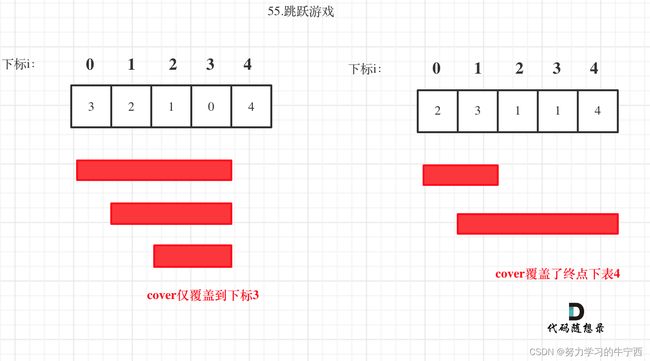
局部最优推出全局最优,找不出反例,试试贪心!如图:
具体代码实现思路
i每次移动只能在cover的范围内移动,每移动一个元素,cover得到该元素数值(新的覆盖范围)的补充,让i继续移动下去;
而cover每次只取 max(该元素数值补充后的范围, cover本身范围),如果cover大于等于了终点下标,直接return true就可以了。
2. 代码实现
# 贪心解法
# time:O(N);space:O(1)
class Solution(object):
def canJump(self, nums):
"""
:type nums: List[int]
:rtype: bool
"""
# 只有一个元素,就是能达到
if len(nums) == 1: return True
cur = 0
cover = 0
# python不支持动态修改for循环中变量,使用while循环代替
# 注意这里是小于等于cover
while cur <= cover:
cover = max(cover, nums[cur]+cur)
# 说明可以覆盖到终点了
if cover >= len(nums)-1:
return True
cur += 1
return False
3. 复杂度分析
时间复杂度:O(N);
需要遍历数组一次;
空间复杂度:O(1)
只有常数个变量来记录;
4. 思考与收获
-
我自己写的时候犯了一个错误,感觉值得记录:
# 错误示例 class Solution(object): def canJump(self, nums): if len(nums) == 1: return True cur = 0 cover = nums[0] while cur <= cover: # cur+1这一行只能放在while循环的最后一句 # 因为当cur=cover进入循环之后,马上又+1 # 会让cur跑到cover外面去 # 所以应该是执行下面的逻辑之前,需要保证cur在cover范围内的 cur += 1 cover = max(cover, nums[cur]+cur) if cover >= len(nums)-1: return True return Falsecur+1这一行只能放在while循环的最后一句;因为当cur=cover进入循环之后,马上又+1;会让cur跑到cover外面去; 所以应该是执行下面的逻辑之前,需要保证cur在cover范围内的;
-
这道题目关键点在于:不用拘泥于每次究竟跳跳几步,而是看覆盖范围,覆盖范围内一定是可以跳过来的,不用管是怎么跳的;大家可以看出思路想出来了,代码还是非常简单的;
-
讲贪心系列的时候,题目和题目之间貌似没有什么联系?是真的就是没什么联系,因为贪心无套路!没有个整体的贪心框架解决一些列问题,只能是接触各种类型的题目锻炼自己的贪心思维!
Reference:代码随想录 (programmercarl.com)
本题学习时间:40分钟。
LeetCode45. 跳跃游戏II
链接:45. 跳跃游戏 II - 力扣(LeetCode)
1. 思路
本题相对于 LeetCode55.跳跃游戏 还是难了不少。但思路是相似的,还是要看最大覆盖范围;本题要计算最小步数,那么就要想清楚什么时候步数才一定要加一呢?
贪心的思路,局部最优:当前可移动距离尽可能多走,如果还没到终点,步数再加一。整体最优:一步尽可能多走,从而达到最小步数。
思路虽然是这样,但在写代码的时候还不能真的就能跳多远跳远,那样就不知道下一步最远能跳到哪里了。
所以真正解题的时候,要从覆盖范围出发,不管怎么跳,覆盖范围内一定是可以跳到的,以最小的步数增加覆盖范围,覆盖范围一旦覆盖了终点,得到的就是最小步数!
这里需要统计两个覆盖范围,当前这一步的最大覆盖和下一步最大覆盖。
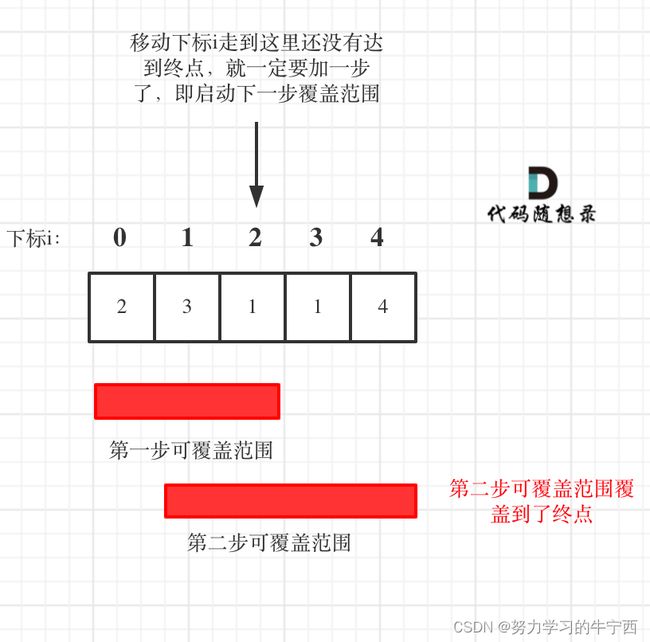
如果移动下标达到了当前这一步的最大覆盖最远距离了,还没有到终点的话,那么就必须再走一步来增加覆盖范围,直到覆盖范围覆盖了终点。
图中覆盖范围的意义在于,只要红色的区域,最多两步一定可以到!(不用管具体怎么跳,反正一定可以跳到)
2. 代码实现
方法一
从图中可以看出来,就是移动下标达到了当前覆盖的最远距离下标时,步数就要加一,来增加覆盖距离。最后的步数就是最少步数。
这里还是有个特殊情况需要考虑,当移动下标达到了当前覆盖的最远距离下标时
- 如果当前覆盖最远距离下标不是是集合终点,步数就加一,还需要继续走。
- 如果当前覆盖最远距离下标就是是集合终点,步数不用加一,因为不能再往后走了。
class Solution(object):
def jump(self, nums):
"""
:type nums: List[int]
:rtype: int
"""
if len(nums) == 1: return 0
ans = 0 # 记录走的最大步数
curDistance = 0 # 当前覆盖最远距离下标
nextDistance = 0 # 下一步覆盖最远距离下标
for i in range(len(nums)):
# 更新下一步覆盖最远距离下标
nextDistance = max(i + nums[i], nextDistance)
# 遇到当前覆盖最远距离下标
if i == curDistance:
# 如果当前覆盖最远距离下标不是终点
if curDistance != len(nums) - 1:
# 需要走下一步
ans += 1
# 更新当前覆盖最远距离下标(相当于加油了)
curDistance = nextDistance
# 下一步的覆盖范围已经可以达到终点,结束循环
if nextDistance >= len(nums) - 1: break
# 当前覆盖最远距离下标是集合终点,不用做ans++操作了,直接结束
return ans
方法二
依然是贪心,思路和方法一差不多,代码可以简洁一些。
针对于方法一的特殊情况,可以统一处理,即:移动下标只要遇到当前覆盖最远距离的下标,直接步数加一,不考虑是不是终点的情况。
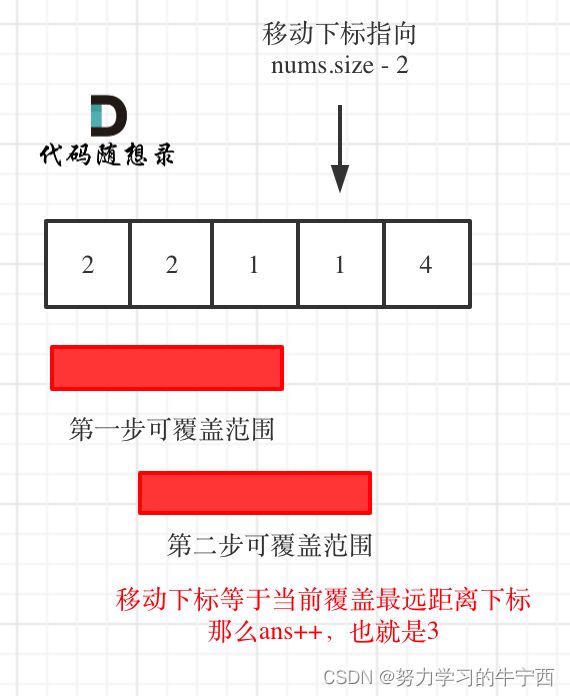
想要达到这样的效果,只要让移动下标,最大只能移动到nums.size - 2的地方就可以了。
因为当移动下标指向nums.size - 2时:
- 如果移动下标等于当前覆盖最大距离下标, 需要再走一步(即ans++),因为最后一步一定是可以到的终点。(题目假设总是可以到达数组的最后一个位置),如图:
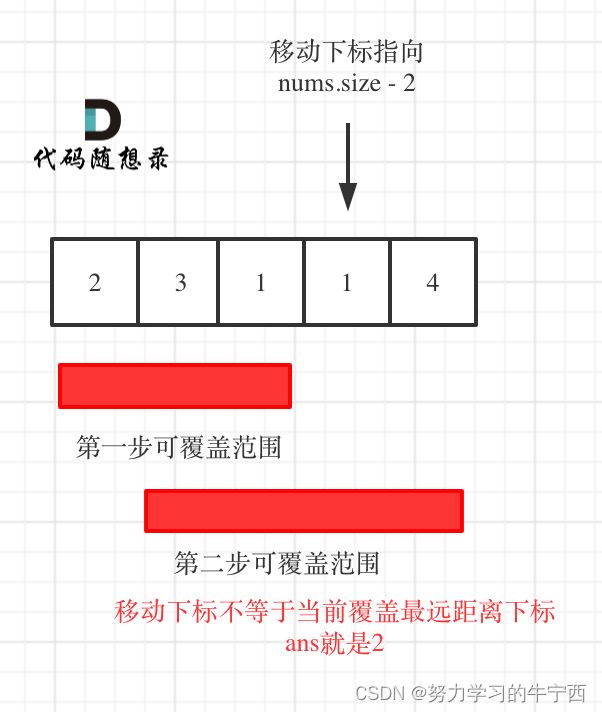
- 如果移动下标不等于当前覆盖最大距离下标,说明当前覆盖最远距离就可以直接达到终点了,不需要再走一步。如图:
实现代码如下:
# 贪心版本二
class Solution:
def jump(self, nums: List[int]) -> int:
if len(nums) == 1:
return 0
curDistance, nextDistance = 0, 0
step = 0
for i in range(len(nums)-1):
nextDistance = max(nextDistance, nums[i]+i)
if i == curDistance:
curDistance = nextDistance
step += 1
return step
可以看出版本二的代码相对于版本一简化了不少!
其精髓在于控制移动下标i只移动到nums.size() - 2的位置,所以移动下标只要遇到当前覆盖最远距离的下标,直接步数加一,不用考虑别的了。
3. 复杂度分析
时间复杂度:O(N);
需要遍历数组一次;
空间复杂度:O(1)
只有常数个变量来记录;
4. 思考与收获
- 这道题目相当于LeetCode55.跳跃游戏难了不止一点;但代码又十分简单,贪心就是这么巧妙;
- 理解本题的关键在于:以最小的步数增加最大的覆盖范围,直到覆盖范围覆盖了终点,这个范围内最小步数一定可以跳到,不用管具体是怎么跳的,不纠结于一步究竟跳一个单位还是两个单位;
Reference:代码随想录 (programmercarl.com)
本题学习时间:120分钟。
本篇学习时间约为3小时,总结字数5000+;是贪心算法相关的三道题,贪心算法没有什么固定的套路,只能多做一些题目,积累贪心算法的思路和经验。(求推荐!)