Codeforces-Gym 104849C：Secure the Top Secret（最小费用最大流）

Problem C. Secure the Top Secret
Time Limit: 2 seconds
You are responsible for the security of ICPC (the Institute for Computer Program Critiques).
The institute is in a one-storied building. Its rectangular floor is partitioned into square sections of the same size in a grid form. Two sections are said to be adjacent if they share an edge.
Some of the sections in the building are blocked. All the sides of a blocked section are walled up and no entry is possible. All the other sections have no walls in between, and adjacent sections normally intercommunicate. However, roll-down shutters are equipped between some of the adjacent sections, so that closing such a shutter makes direct moves between the two sections impossible.
The top-secret research is being conducted in one of the outermost sections of the building.
The section is called the top-secret section. The building has only one entrance at one of its outermost sections, which should be the only entry to the building. However, you have noticed that a window of one of the outermost sections is so fragile that it may allow trespassers to enter the building.
You must secure the top secret from trespassers. To do so, you may have to close some of the shutters so that breaking two or more closed shutters is required to make a route from the section with the fragile window to the top-secret section. In addition, there should exist at least one route from the entrance section to the top-secret section with no shutters closed on it.
You are to write a program that finds the minimum number of shutters to close to secure the top secret.
Input
The input consists of a single test case of the following format.
$$\begin{gathered} nm \\ {s}_1 \\ . \\ . \\ . \\ {s}_n \\ k \\ {r}_1{c}_1{d}_1 \\ . \\ . \\ . \\ {r}_k{c}_k{d}_k \end{gathered}$$
$n$ and $m$ are integers between $2$ and $100$, inclusive, representing that the building floor has $n$ rows and $m$ columns of sections. The section in the $j$-th column of the $i$-th row is identified as section $(i,j)$. The $i$-th line of the following $n$ lines has a string $s_i$ of length $m$ describing the sections in the $i$-th row. Each character of $s_i$ is one of $.$, $\#$, $S$, $T$, and $U$. If the $j$-th character of $s_i$ is $\#$, section $(i,j)$ is blocked and is impassable; otherwise, the section is passable. The $j$-th character of $s_i$ being $S$ means that section $(i,j)$ is the entrance section, $T$ means the top-secret section, and $U$ means the entry point of the trespassers, that is, the section with a fragile window.
Each of $S$, $T$, and $U$ occurs exactly once in the input as an outermost section. The top-secret section is reachable from the entrance through passable sections with no shutters closed.
$k$ is the number of the shutters in the building. The $i$-th line in the following $k$ lines describes a shutter by two integers $r_i$ and $c_i$, and a character $d_i$. $d_i$ is either $r$ or $b$. If $d_i$ is $r$, $1\le ri\le n$ and $1\le c_i<$ m hold, and a shutter is equipped between sections $(r_i,c_i)$ and $(r_i,c_i+1)$. If $d_i$ is $b$, $1\le r_i<n$ and $1\le c_i\le m$ hold, and a shutter is equipped between sections $(r_i,c_i)$ and $(r_i+1,c_i)$. The same combination of $r_i$, $c_i$, and $d_i$ appears only once. Each shutter is equipped only between two unblocked adjacent sections.

Output
Output a single integer in a line which is the minimum number of shutters to close to secure the top secret. If that is not possible, output $-1$. If trespassing to the top-secret section is not possible with all shutters open, output $0$.

Sample Input 1
3 3
S…
#…
U.T
7
1 2 b
1 3 b
2 2 b
2 2 r
2 3 b
3 1 r
3 2 r
Sample Output 1
3

Sample Input 2
2 2
ST
.U
4
1 1 r
1 1 b
1 2 b
2 1 r
Sample Output 2
-1

Sample Input 3
7 10
U…
…
###…
…
…###
…
S…T
18
4 4 r
5 4 r
6 7 r
7 7 r
3 4 b
3 5 b
3 6 b
3 7 b
3 8 b
3 9 b
3 10 b
5 1 b
5 2 b
5 3 b
5 4 b
5 5 b
5 6 b
5 7 b
Sample Output 3
14

Sample Input 1 is depicted in the following figure. The dotted lines represent where the shutters are equipped.

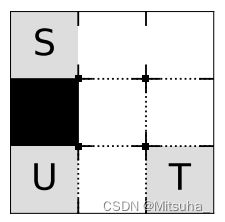
思路:直觉感觉像是网络流，如何建图是关键。

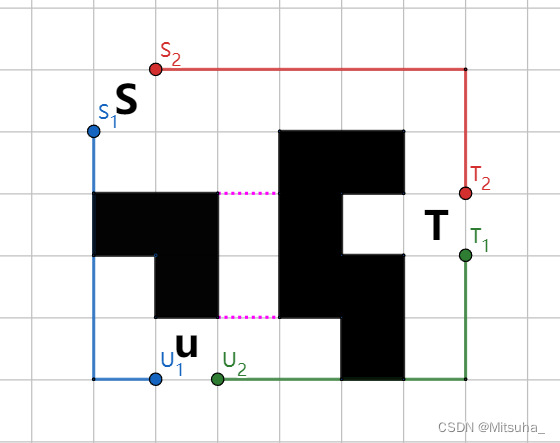
如上图所示，黑色方块为障碍物，虚线代表百叶窗。
$S,T,U$会把地图拆分为蓝、红、绿3个区域，其中$S,T$点互相连通。
要满足题目条件，我们只需将蓝色区域和绿色区域连通起来，且绿色区域和蓝色区域均不能与红色连通，否则会阻断$S$和$T$的连通。
那么接下来只需要以$U_1$和$U_2$分别作为源点和汇点来建图，障碍物的边作为容量无限费用为0的边，虚线作为容量为1费用为1的边。
最后跑个流量为$2$最小费用最大流即可。复杂度$O(n\ast m{\log }_2(n\ast m))$。

#include
#define fi first
#define se second
#define lson (k<<1)
#define rson (k<<1)+1
#define mid ((l+r)/2)
#define sz(x) int(x.size())
#define pii pair<ll,ll>
#define bit bitset<100000>
using namespace std;
const int MAX=2e6+10;
const int MOD=1e9+7;
const int INF=INT_MAX/2;
const double PI=acos(-1.0);
typedef long long ll;
struct edg{int from,to,cap,cost,rev;};
class MCMF
{
    struct node
    {
        int x,dis,flow;
        bool operator<(const node& q) const {return q.dis<dis;}
    };
private:
    int s,t;
    vector<int>h,d,v;
    vector<edg*>p;
    vector<vector<edg>>g;
private:
    void Spfa() { //worst O(n*m)
        fill(h.begin(),h.end(),INF);
        fill(v.begin(),v.end(),0);
        queue<int>q;
        q.push(s);
        h[s]=0;
        while(!q.empty())
        {
            int x=q.front();q.pop();
            v[x]=0;
            for(auto &e:g[x])
            {
                int y=e.to;
                if(!e.cap||h[y]<=h[x]+e.cost)continue;
                h[y]=h[x]+e.cost;
                if(v[y])continue;
                v[y]=1;
                q.push(y);
            }
        }
    }
    int Dijkstra(int flow) //O(m*log(n))
    {
        fill(v.begin(),v.end(),0);
        fill(d.begin(),d.end(),-1);
        fill(p.begin(),p.end(),nullptr);
        priority_queue<node> q;
        q.push({s,0,flow});
        d[s]=0;
        int ret=0;
        while(!q.empty())
        {
            auto cur=q.top();q.pop();
            int x=cur.x;
            if(d[x]!=cur.dis)continue;
            if(x==t)ret=cur.flow; //因为没有构造势能h,不能直接return
            for(auto &e:g[x])
            {
                int y=e.to;
                if(e.cap<=0)continue;
                if(d[y]!=-1&&d[y]<=d[x]+e.cost+h[x]-h[y])continue;
                d[y]=d[x]+e.cost+h[x]-h[y];
                p[y]=&e;
                q.push({y,d[y],min(cur.flow,e.cap)});
            }
        }
        return ret;
    }
public:
    explicit MCMF(int _n,int _s,int _t)
    {
        s=_s,t=_t;
        h.resize(_n);d.resize(_n);
        v.resize(_n);p.resize(_n);g.resize(_n);
    }
    void AddEdg(int from,int to,int cap,int cost) {
        g[from].push_back((edg){from,to,cap,cost,sz(g[to])});
        g[to].push_back((edg){to,from,0,-cost,sz(g[from])-1});
    }
    pii MinCostMaxFlow(int flow)
    {
//        Spfa();
        fill(h.begin(),h.end(),0);
        int mf=0,mc=0,f=0;
        while(f=Dijkstra(flow))
        {
            for(int i=0;i<sz(v);i++)h[i]+=d[i]; //update h
            for(int i=t;p[i];i=p[i]->from)      //update cap
            {
                p[i]->cap-=f;
                g[p[i]->to][p[i]->rev].cap+=f;
            }
            flow-=f;
            mf+=f;
            mc+=f*h[t];
        }
        return {mf,mc};
    }
};
int p[110*110];
int f(int x){return p[x]==x?x:p[x]=f(p[x]);}
char s[110][110];
auto Find(set<int> v[3])
{
    int src=-1,dst=-1,tag=-1;
    for(int x:v[0])
    for(int y:v[1])
    {
        if(f(x)!=f(y))continue;
        for(int z:v[2])if(f(x)!=f(z)){tag=f(x);break;}
        if(tag<0)continue;
        v[0].insert(v[1].begin(),v[1].end());
        for(int z:v[2])
        for(int i:v[0])
        {
            if(f(z)!=f(i))continue;
            if(src==-1)src=z;
            else dst=z;
            break;
        }
        return make_tuple(src,dst,tag);
    }
    return make_tuple(src,dst,tag);
}
int solve()
{
    int n,m;
    cin>>n>>m;
    for(int i=0;i<n;i++)scanf("%s",s+i);
    for(int i=0;i<(n+1)*(m+1);i++)p[i]=i;
    auto id=[m](int x,int y){return x*(m+1)+y;};
    set<pii>e;
    set<int>v[3];
    for(int i=0;i<n;i++)
    for(auto j:{0,m-1})
    {
        int c=j+(j>0);
        if(s[i][j]=='S'){v[0].insert({id(i,c),id(i+1,c)});continue;}
        if(s[i][j]=='T'){v[1].insert({id(i,c),id(i+1,c)});continue;}
        if(s[i][j]=='U'){v[2].insert({id(i,c),id(i+1,c)});continue;}
        p[f(id(i,c))]=f(id(i+1,c));
        e.insert({id(i,c),id(i+1,c)});
    }
    for(auto i:{0,n-1})
    for(int j=0;j<m;j++)
    {
        int r=i+(i>0);
        if(s[i][j]=='S'){v[0].insert({id(r,j),id(r,j+1)});continue;}
        if(s[i][j]=='T'){v[1].insert({id(r,j),id(r,j+1)});continue;}
        if(s[i][j]=='U'){v[2].insert({id(r,j),id(r,j+1)});continue;}
        p[f(id(r,j))]=f(id(r,j+1));
        e.insert({id(r,j),id(r,j+1)});
    }
    for(int i=0;i<n;i++)
    for(int j=0;j<m;j++)
    {
        if(s[i][j]!='#')continue;
        p[f(id(i,j))]=f(id(i+1,j));
        p[f(id(i,j))]=f(id(i,j+1));
        p[f(id(i,j))]=f(id(i+1,j+1));
        e.insert({id(i,j),id(i+1,j)});
        e.insert({id(i,j),id(i,j+1)});
        e.insert({id(i,j),id(i+1,j+1)});
    }
    int src=-1,dst=-1,tag=-1;
    tie(src,dst,tag)=Find(v);
    assert(src!=-1&&dst!=-1&&tag!=-1);

    MCMF mcmf((n+1)*(m+1),src,dst);
    for(auto kv: e)
    {
        mcmf.AddEdg(kv.fi,kv.se,INF,0);
        mcmf.AddEdg(kv.se,kv.fi,INF,0);
    }
    int q;
    cin>>q;
    while(q--)
    {
        int x,y;char d;
        scanf("%d%d %c",&x,&y,&d);
        int u=d=='r'?id(x-1,y):id(x,y-1);
        int v=id(x,y);
        if(f(u)==tag||f(v)==tag)continue;
        mcmf.AddEdg(u,v,1,1);
        mcmf.AddEdg(v,u,1,1);
    }
    auto ans=mcmf.MinCostMaxFlow(2);
    return printf("%d\n",ans.fi==2?ans.se:-1);
}
int main()
{
    int T=1;
    //cin>>T;
    while(T--)solve();
    return 0;
}