Redis经典五大类型源码及底层实现（二）

• 作者简介：大家好，我是爱吃芝士的土豆倪，24届校招生Java选手，很高兴认识大家
• 系列专栏：Spring源码、JUC源码、Kafka原理、分布式技术原理、数据库技术
• 如果感觉博主的文章还不错的话，请三连支持一下博主哦
• 博主正在努力完成2023计划中：源码溯源，一探究竟
• 联系方式：nhs19990716，加我进群，大家一起学习，一起进步，一起对抗互联网寒冬

Redis经典五大类型源码及底层实现

Hash数据结构介绍

redis7

listpack+hashtable

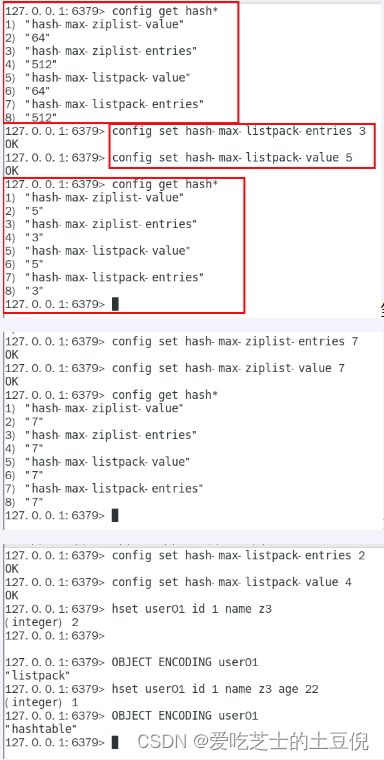
hash-max-listpack-entries：使用压缩列表保存时哈希集合中的最大元素个数。

hash-max-listpack-value：使用压缩列表保存时哈希集合中单个元素的最大长度。

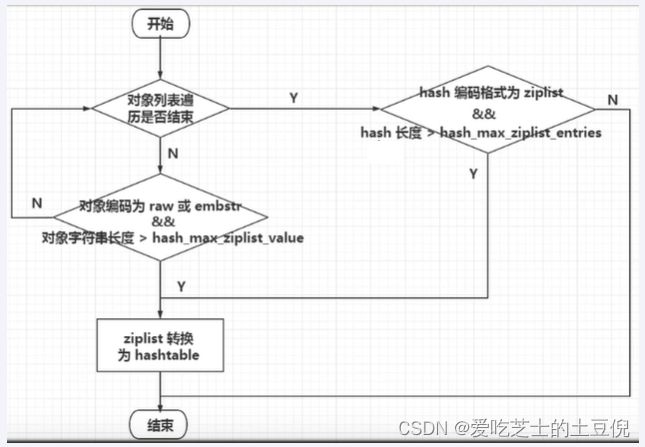
Hash类型键的字段个数 小于 hash-max-listpack-entries且每个字段名和字段值的长度 小于 hash-max-listpack-value 时，

Redis才会使用OBJ_ENCODING_LISTPACK来存储该键，前述条件任意一个不满足则会转换为 OBJ_ENCODING_HT的编码方式

结论：

1.哈希对象保存的键值对数量小于512个

2.所有的键值对的键和值的字符串长度都小于等于64byte（一个英文字母一个字节）时用listpack，反之用hashtable

3.listpack升级到hashtable可以，反过来降级不可以

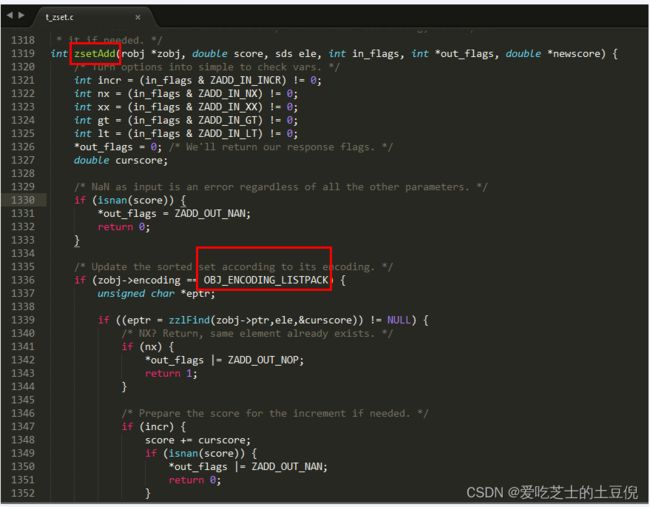
源码分析

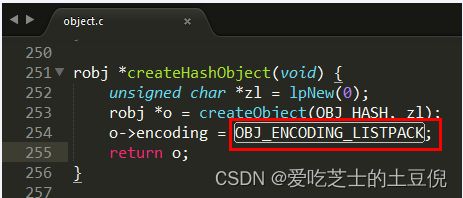
实现：object.c

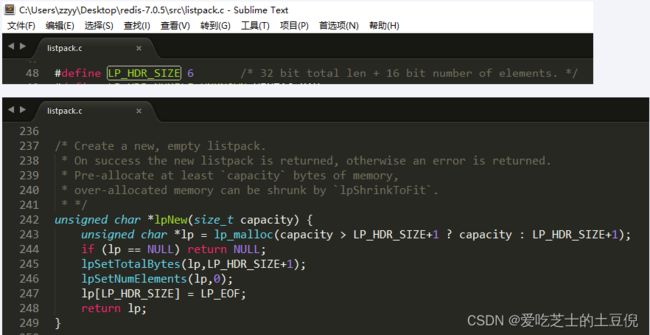
实现：listpack.c

lpNew 函数创建了一个空的 listpack，一开始分配的大小是 LP_HDR_SIZE 再加 1 个字节。LP_HDR_SIZE 宏定义是在 listpack.c 中，它默认是 6 个字节，其中 4 个字节是记录 listpack 的总字节数，2 个字节是记录 listpack 的元素数量。

此外，listpack 的最后一个字节是用来标识 listpack 的结束，其默认值是宏定义 LP_EOF。

和 ziplist 列表项的结束标记一样，LP_EOF 的值也是 255

实现：object.c

明明已经有ziplist了，为什么出来一个listpack紧凑列表呢？

ziplist的连锁更新问题

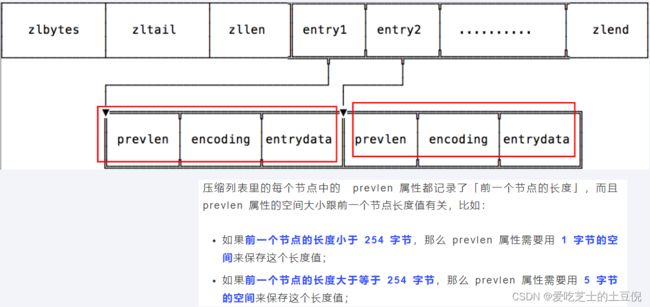
压缩列表新增某个元素或修改某个元素时，如果空间不不够，压缩列表占用的内存空间就需要重新分配。而当新插入的元素较大时，可能会导致后续元素的 prevlen 占用空间都发生变化，从而引起「连锁更新」问题，导致每个元素的空间都要重新分配，造成访问压缩列表性能的下降。

案例说明：压缩列表每个节点正因为需要保存前一个节点的长度字段，就会有连锁更新的隐患

第一步：现在假设一个压缩列表中有多个连续的、长度在 250～253 之间的节点，如下图：

因为这些节点长度值小于 254 字节，所以 prevlen 属性需要用 1 字节的空间来保存这个长度值，一切OK，O(∩_∩)O哈哈~

第二步：这时，如果将一个长度大于等于 254 字节的新节点加入到压缩列表的表头节点，即新节点将成为entry1的前置节点，如下图：

因为entry1节点的prevlen属性只有1个字节大小，无法保存新节点的长度，此时就需要对压缩列表的空间重分配操作并将entry1节点的prevlen 属性从原来的 1 字节大小扩展为 5 字节大小。

第三步：连续更新问题出现

entry1节点原本的长度在250～253之间，因为刚才的扩展空间，此时entry1节点的长度就大于等于254，因此原本entry2节点保存entry1节点的 prevlen属性也必须从1字节扩展至5字节大小。entry1节点影响entry2节点，entry2节点影响entry3节点…一直持续到结尾。这种在特殊情况下产生的连续多次空间扩展操作就叫做「连锁更新」

结论：listpack 是 Redis 设计用来取代掉 ziplist 的数据结构，它通过每个节点记录自己的长度且放在节点的尾部，来彻底解决掉了 ziplist 存在的连锁更新的问题

listpack结构

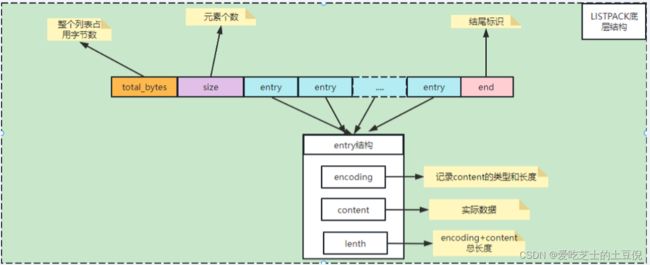
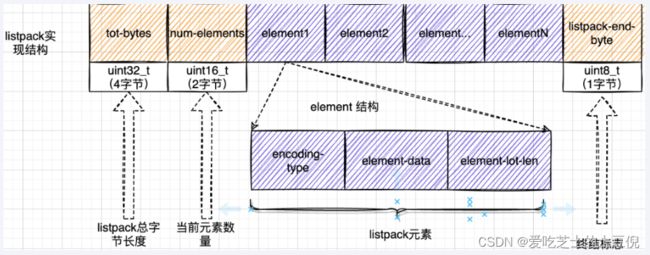
Total Bytes	为整个listpack的空间大小，占用4个字节，每个listpack最多占用4294967295Bytes。
num-elements	为listpack中的元素个数，即Entry的个数占用2个字节
element-1~element-N	为每个具体的元素
listpack-end-byte	为listpack结束标志，占用1个字节，内容为0xFF。

entry结构

• 当前元素的编码类型
• 元素数据
• 以及编码类型和元素数据这两部分的长度

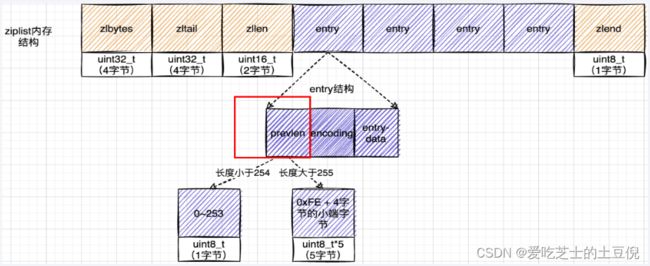
ziplist内存布局 VS listpack内存布局

和ziplist 列表项类似，listpack 列表项也包含了元数据信息和数据本身。不过，为了避免ziplist引起的连锁更新问题，listpack 中的每个列表项

不再像ziplist列表项那样保存其前一个列表项的长度。

List数据结构

Redis6

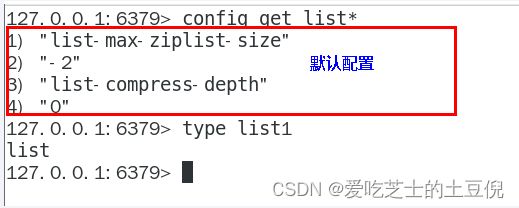
(1) ziplist压缩配置：list-compress-depth 0

​ 表示一个quicklist两端不被压缩的节点个数。这里的节点是指quicklist双向链表的节点，而不是指ziplist里面的数据项个数

参数list-compress-depth的取值含义如下：

0: 是个特殊值，表示都不压缩。这是Redis的默认值。

1: 表示quicklist两端各有1个节点不压缩，中间的节点压缩。

2: 表示quicklist两端各有2个节点不压缩，中间的节点压缩。

3: 表示quicklist两端各有3个节点不压缩，中间的节点压缩。

依此类推…

(2) ziplist中entry配置：list-max-ziplist-size -2

当取正值的时候，表示按照数据项个数来限定每个quicklist节点上的ziplist长度。比如，当这个参数配置成5的时候，表示每个quicklist节点的ziplist最多包含5个数据项。当取负值的时候，表示按照占用字节数来限定每个quicklist节点上的ziplist长度。这时，它只能取-1到-5这五个值，

每个值含义如下：

-5: 每个quicklist节点上的ziplist大小不能超过64 Kb。（注：1kb => 1024 bytes）

-4: 每个quicklist节点上的ziplist大小不能超过32 Kb。

-3: 每个quicklist节点上的ziplist大小不能超过16 Kb。

-2: 每个quicklist节点上的ziplist大小不能超过8 Kb。（-2是Redis给出的默认值）

-1: 每个quicklist节点上的ziplist大小不能超过4 Kb。

Redis版本前List的一种编码格式

list用quicklist存储，quicklist存储了一个双向链表，每个节点都是一个ziplist

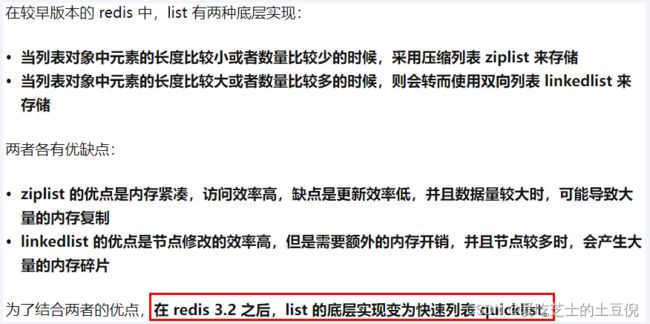
在Redis3.0之前，list采用的底层数据结构是ziplist压缩列表+linkedList双向链表

然后在高版本的Redis中底层数据结构是quicklist(替换了ziplist+linkedList)，而quicklist也用到了ziplist

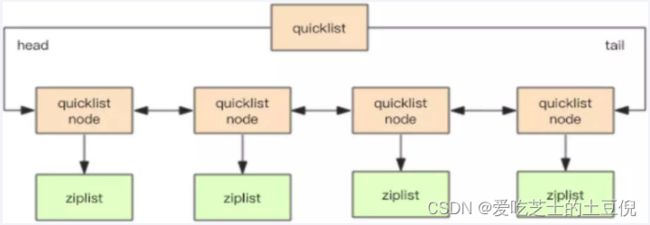
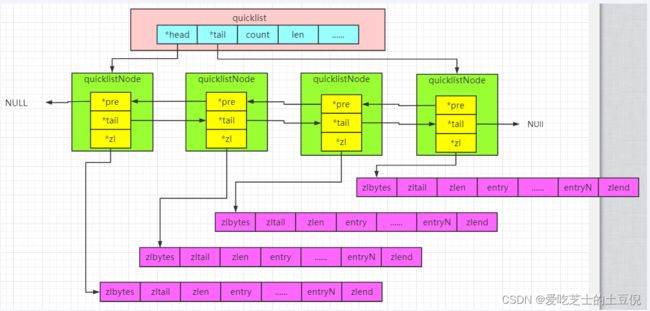
结论：quicklist就是「双向链表 + 压缩列表」组合，因为一个 quicklist 就是一个链表，而链表中的每个元素又是一个压缩列表

quicklist 实际上是 zipList 和 linkedList 的混合体，它将 linkedList按段切分，每一段使用 zipList 来紧凑存储，多个 zipList 之间使用双向指针串接起来。

源码分析

quicklist.h，head和tail指向双向列表的表头和表尾

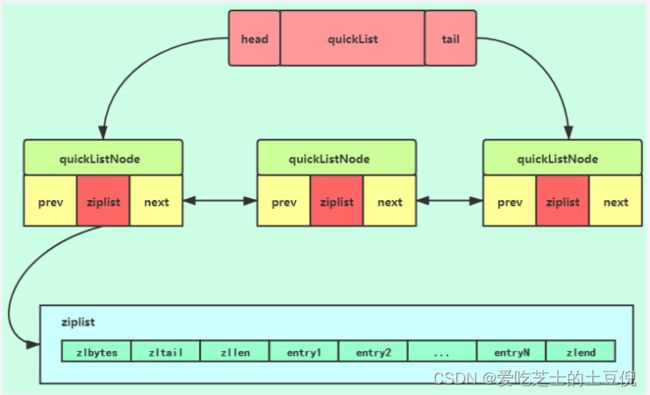
quicklist结构

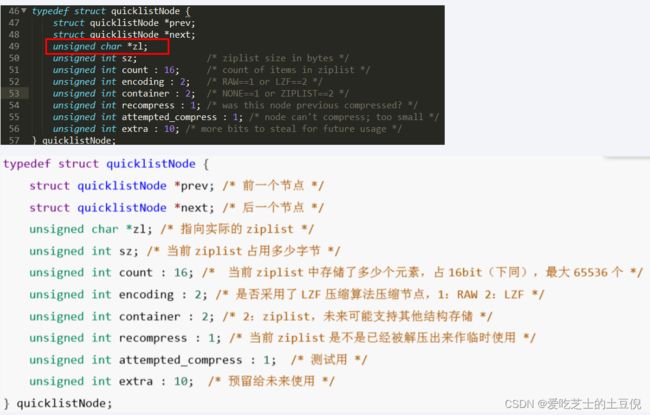
quicklistNode结构

quicklistNode中的*zl指向一个ziplist，一个ziplist可以存放多个元素

Redis7

listpack紧凑列表

是用来替代 ziplist 的新数据结构，在 7.0 版本已经没有 ziplist 的配置了（6.0版本仅部分数据类型作为过渡阶段在使用）

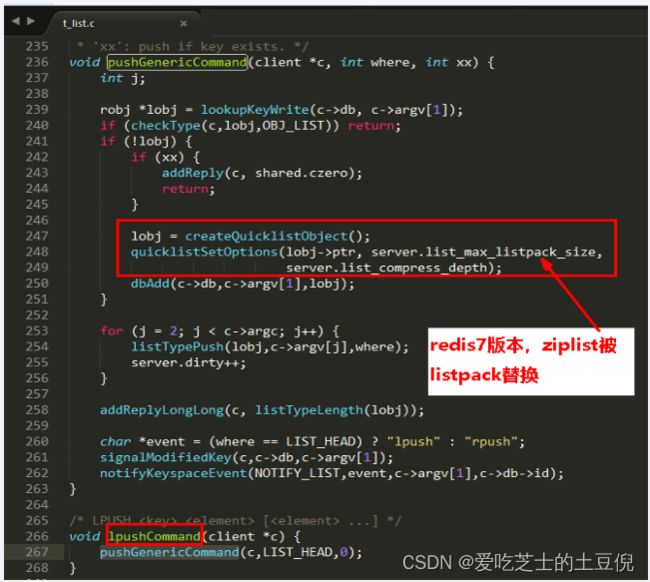
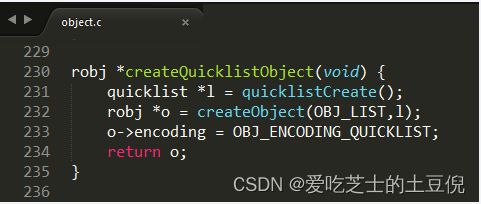
源码实现

本图最下方有lpush命令执行后直接调用pushGenericCommand命令

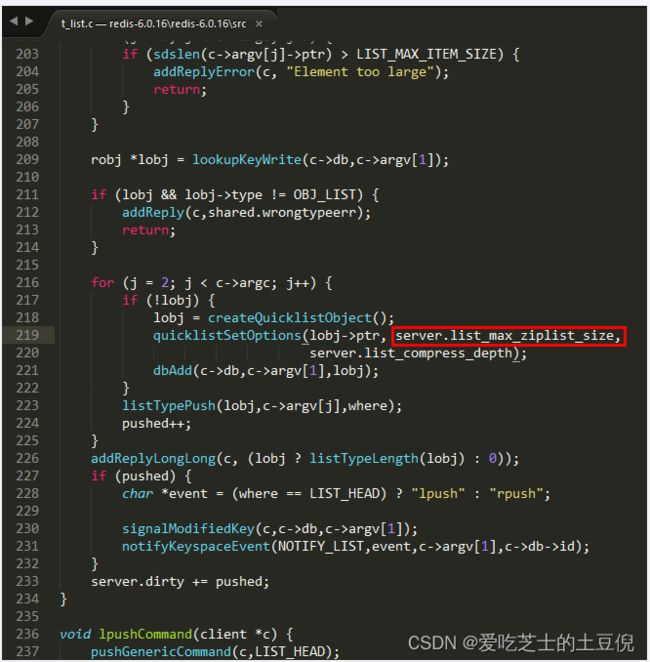
看看redis6的相同文件t_list.c

实现：object.c

Redis7的List的一种编码格式，list用quicklist存储，quicklist存储了一个双向链表，每个节点都是一个listpack

quicklist是listpack和linkedlist的结合体

Set数据结构介绍

Redis用intset或hashtable存储set。如果元素都是整数类型，就用intset存储。

如果不是整数类型，就用hashtable（数组+链表的存来储结构）。key就是元素的值，value为null。

Set的两种编码格式

intset

hashtable

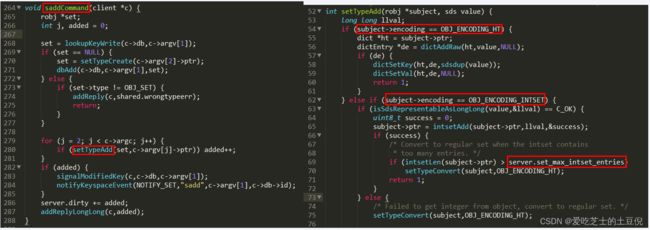
源码分析

ZSet数据结构介绍

Redis6

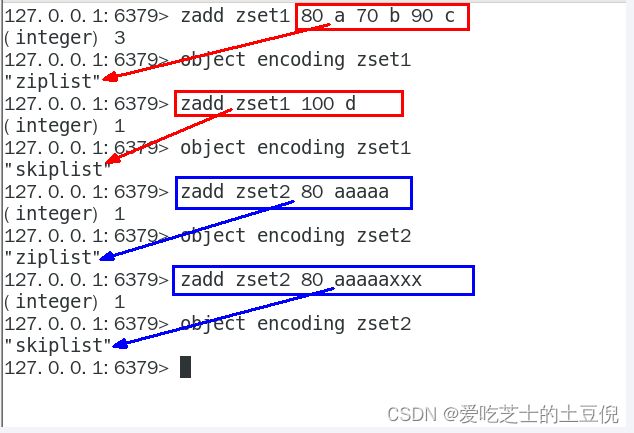
当有序集合中包含的元素数量超过服务器属性 server.zset_max_ziplist_entries 的值（默认值为 128 ），

或者有序集合中新添加元素的 member 的长度大于服务器属性 server.zset_max_ziplist_value 的值（默认值为 64 ）时，

redis会使用跳跃表作为有序集合的底层实现。

否则会使用ziplist作为有序集合的底层实现

Redis7

ZSet的两种编码格式

redis6：ziplist + skiplist

redis7：listpack + skiplist

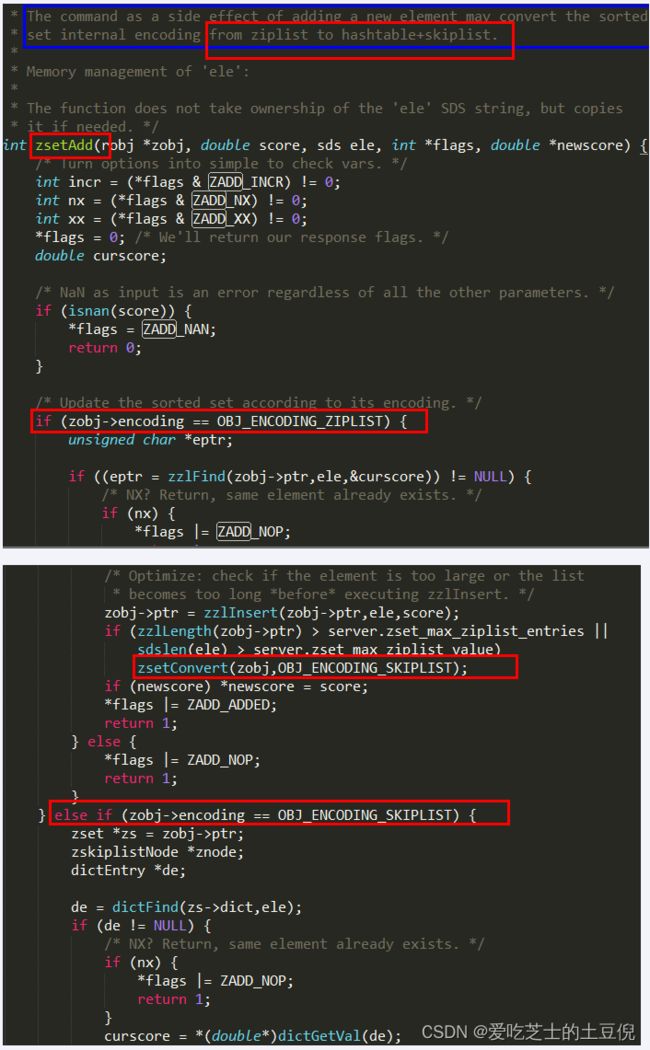
源码分析

Redis6

Redis7

skiplist

为什么引出跳表

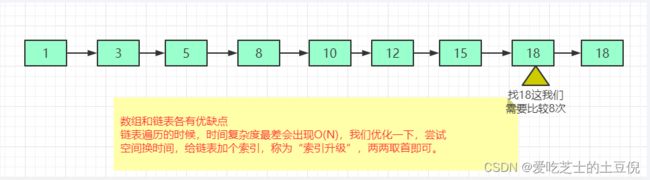
先从一个单链表来讲

对于一个单链表来讲，即便链表中存储的数据是有序的，如果我们要想在其中查找某个数据，也只能从头到尾遍历链表。

这样查找效率就会很低，时间复杂度会很高O(N)

但是存在痛点：

解决方法：升维，也叫空间换时间。

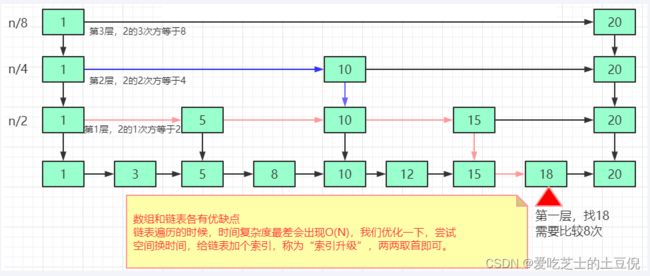
优化

从这个例子里，我们看出，加来一层索引之后，查找一个结点需要遍历的结点个数减少了，也就是说查找效率提高了。

优化二

画一个包含64个节点的链表，按照前面讲的这种思路，建立五级索引

是什么？

skiplist是一种以空间换取时间的结构。

由于链表，无法进行二分查找，因此借鉴数据库索引的思想，提取出链表中关键节点（索引），先在关键节点上查找，再进入下层链表查找，提取多层关键节点，就形成了跳跃表

but

由于索引也要占据一定空间的，所以，索引添加的越多，空间占用的越多

总体来讲 跳表 = 链表 + 多级索引

跳表时间 + 空间复杂度介绍

时间复杂度

跳表查询的时间复杂度分析，如果链表里有N个结点，会有多少级索引呢？

按照我们前面讲的，两两取首。每两个结点会抽出一个结点作为上一级索引的结点，以此估算：

第一级索引的结点个数大约就是n/2，

第二级索引的结点个数大约就是n/4，

第三级索引的结点个数大约就是n/8，依次类推…

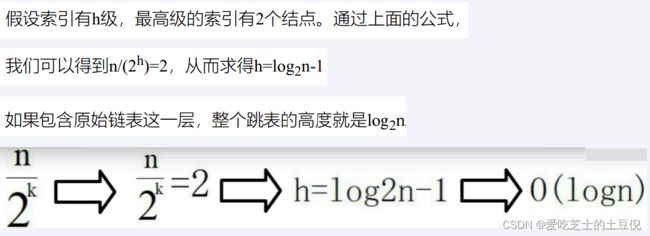
也就是说，第k级索引的结点个数是第k-1级索引的结点个数的1/2，那第k级索引结点的个数就是n/(2^k)

空间复杂度

跳表查询的空间复杂度分析

比起单纯的单链表，跳表需要存储多级索引，肯定要消耗更多的存储空间。那到底需要消耗多少额外的存储空间呢？

我们来分析一下跳表的空间复杂度。

第一步：首先原始链表长度为n，

第二步：两两取首，每层索引的结点数：n/2, n/4, n/8 … , 8, 4, 2 每上升一级就减少一半，直到剩下2个结点,以此类推；如果我们把每层索引的结点数写出来，就是一个等比数列。

这几级索引的结点总和就是n/2+n/4+n/8…+8+4+2=n-2。所以，跳表的空间复杂度是O(n) 。也就是说，如果将包含n个结点的单链表构造成跳表，我们需要额外再用接近n个结点的存储空间。

第三步：思考三三取首，每层索引的结点数：n/3, n/9, n/27 … , 9, 3, 1 以此类推；

第一级索引需要大约n/3个结点，第二级索引需要大约n/9个结点。每往上一级，索引结点个数都除以3。为了方便计算，我们假设最高一级的索

引结点个数是1。我们把每级索引的结点个数都写下来，也是一个等比数列

通过等比数列求和公式，总的索引结点大约就是n/3+n/9+n/27+…+9+3+1=n/2。尽管空间复杂度还是O(n) ，但比上面的每两个结点抽一个结点的索引构建方法，要减少了一半的索引结点存储空间。

所以空间复杂度是O(n)；

优缺点

优点：

跳表是一个最典型的空间换时间解决方案，而且只有在数据量较大的情况下才能体现出来优势。而且应该是读多写少的情况下才能使用，所以它的适用范围应该还是比较有限的

缺点：

维护成本相对要高，

在单链表中，一旦定位好要插入的位置，插入结点的时间复杂度是很低的，就是O(1)

but

新增或者删除时需要把所有索引都更新一遍，为了保证原始链表中数据的有序性，我们需要先找

到要动作的位置，这个查找操作就会比较耗时最后在新增和删除的过程中的更新，时间复杂度也是O(log n)