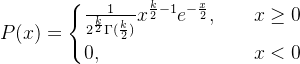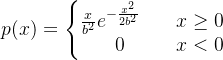基于MATLAB的卡方分布，瑞利分布，T与F分布（附完整代码与例题）

一. 卡方分布

1.1 数学理论

首先我们来看下伽玛分布的概率密度函数：

其中：

令，就可以得到一个新的分布，这个分布在概率论上被叫做卡方分布。卡方分布也可以写做分布。其概率密度函数则为：

卡方分布要求参数k为正整数。

1.2 MATLAB函数

y=chi2pdf(x,k)
%卡方分布概率密度函数

F=chi2cdf(x,k)
%卡方分布概率分布函数

x=chi2inv(F,k)
%逆卡方分布概率分布函数

有关概率密度函数和概率分布函数的区别，可以看这篇博客：

基于MATLAB的泊松分布，正态分布与伽玛分布（附完整代码与例题）-CSDN博客

1.3 例题

分别绘制出k为1,2,3,4,5时分布的概率密度函数与分布函数曲线。

MATLAB代码：

x=[-eps:-0.02:-0.5,0:0.02:2]; %画图x轴，其中0.02代表画点间隔
x=sort(x'); %对列向量x'进行升序排列
k1=[1,2,3,4,5]; y1=[]; y2=[];
for i=1:length(k1)
    y1=[y1,chi2pdf(x,k1(i))]; 
    y2=[y2,chi2cdf(x,k1(i))];
end
plot(x,y1), figure; plot(x,y2)

概率密度函数：

分布函数曲线：

二. T分布

2.1 数学理论

T分布的概率密度函数为：

其中k为参数，且要求k为正整数。

2.2 MATLAB函数

y=tpdf(x,k)
%T分布概率密度函数

F=tcdf(x,k)
%T分布概率分布函数

x=tinv(F,k)
%逆T分布概率分布函数

2.3 例题

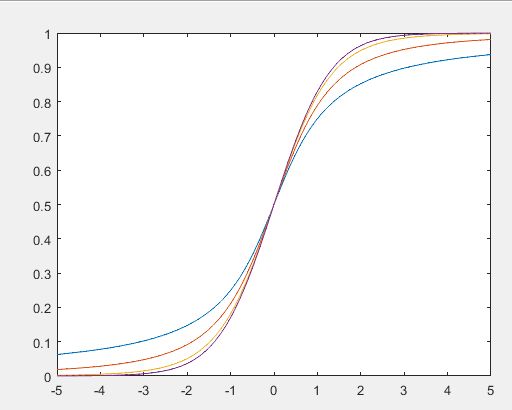
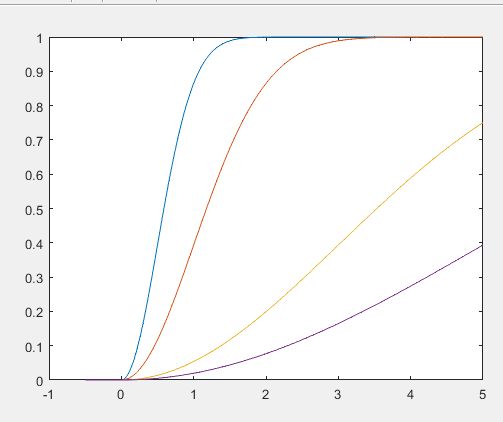
分别绘制出k为1,2,5,10时T分布的概率密度函数与分布函数曲线。

MATLAB代码：

x=[-5:0.02:5]'; 
k1=[1,2,5,10]; 
y1=[];
y2=[];
for i=1:length(k1)
    y1=[y1,tpdf(x,k1(i))];
    y2=[y2,tcdf(x,k1(i))];
end
plot(x,y1), figure; plot(x,y2)

运行结果：

三. 瑞利分布(Rayleigh分布）

3.1 数学理论

Rayleigh分布的概率密度函数为：

3.2 MATLAB函数

y=raylpdf(x,b)
%瑞利分布概率密度函数

F=raylcdf(x,b)
%瑞利分布概率分布函数

x=raylinv(F,b)
%逆瑞利分布概率分布函数

3.3 例题

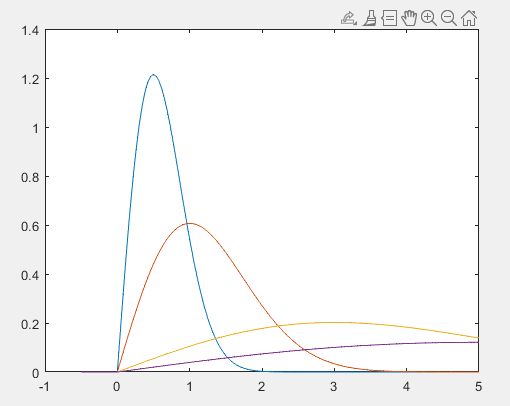
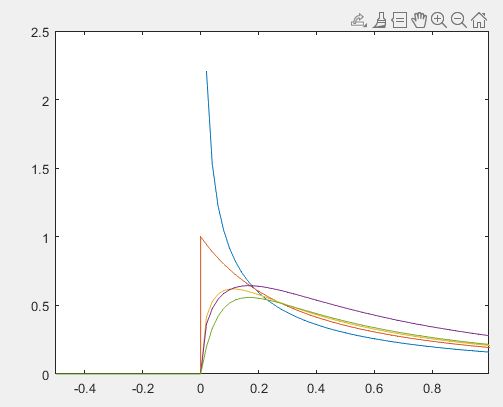
分别绘制b=0.5,1,3,5时Rayleigh分布的概率密度函数与分布函数曲线。

MATLAB代码：

x=[-eps:-0.02:-0.5,0:0.02:5]; 
x=sort(x');
b1=[.5,1,3,5]; y1=[]; y2=[];
for i=1:length(b1)
    y1=[y1,raylpdf(x,b1(i))]; 
    y2=[y2,raylcdf(x,b1(i))]; 
end
plot(x,y1), figure; 
plot(x,y2)

运行结果：

四. F分布

4.1 数学理论

F分布的概率密度函数为：

其中p和q均为参数，且为正整数。

4.2 MATLAB函数

y=fpdf(x,p,q)
%F分布概率密度函数

F=fcdf(x,p,q)
%F分布概率分布函数

x=flinv(F,p.q)
%逆F分布概率分布函数

4.3 例题

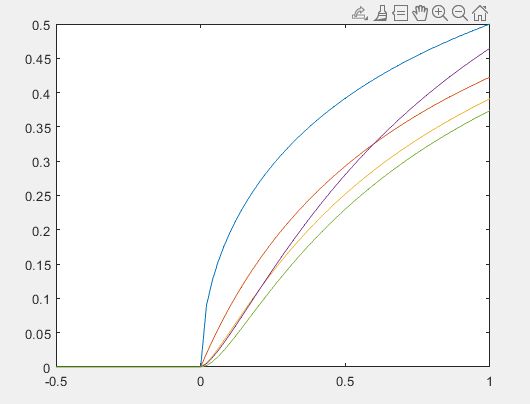
分别绘制(p,q)为(1,1),(2,1),(3,1),(3,2),(4,1)时F分布的概率密度函数与分布函数曲线。

MATLAB代码：

x=[-eps:-0.02:-0.5,0:0.02:1]; 
x=sort(x');
p1=[1 2 3 3 4]; 
q1=[1 1 1 2 1]; 
y1=[];
y2=[];
for i=1:length(p1)
    y1=[y1,fpdf(x,p1(i),q1(i))];
    y2=[y2,fcdf(x,p1(i),q1(i))];
end
plot(x,y1), figure;
plot(x,y2)

运行结果：

五. 概率问题小结

求之内的概率之和：

求之间的概率：

求之间的概率之和：

可以观察到以上三个概率范围都可以直接调用cdf函数解决。

例题1

已知某随机变量x为Rayleigh分布，且b=1，分别求出该随机变量x值落入区间[0.2,2]及区间的概率。

解：

MATLAB代码：

b=1;
p1=raylcdf(0.2,b); %负无穷大到0.2的概率之和 
p2=raylcdf(2,b); %负无穷大到2的概率之和
P1=p2-p1 %0.2~2之间的概率

p1=raylcdf(1,b);
P2=1-p1 %1~正无穷大概率之和

运行结果：

P1 =

    0.8449

P2 =

    0.6065
 

例题2

二维随机变量的联合概率密度为：

求条件概率

解：

写代码之前，我们先简单分析下。条件概率公式告诉我们，其等于联合概率除以P(y)，可得：

观察题目给的联合概率密度发现，x概率有效的部分只有0~1/2,y概率有效的部分也是只有0~1/2。好了，接下来，我们只需要借助MATLAB代码求出这两个概率，再相除即可：

syms x y; %声明变量
f=x^2+x*y/3; 
P1=int(int(f,x,0,1/2),y,0,1/2); %分子部分的联合概率
P2=int(int(f,x,0,1),y,0,1/2) ;%求分母部分，y的概率。x此时为全概率
P=P1/P2

运行结果：

P =
 
5/36