字节校园精选 66 道高频经典笔面试题（含多种思路）（上）

前言

该算法链接来源于
冲刺春招-精选笔面试 66 题大通关

以下为我的学习笔记以及汇总，也为了方便其他人更加快速的浏览

第一天

21. 合并两个有序链表（简单）

将两个升序链表合并为一个新的 升序 链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。

示例 1：

输入：l1 = [1,2,4], l2 = [1,3,4]
输出：[1,1,2,3,4,4]

示例 2：

输入：l1 = [], l2 = []
输出：[]

示例 3：

输入：l1 = [], l2 = [0]
输出：[0]

提示：

两个链表的节点数目范围是 [0, 50]
-100 <= Node.val <= 100
l1 和 l2 均按 非递减顺序 排列

思路
通过递归遍历合并两个有序链表

        if(list1 == null){
            return list2;
        }else if(list2 == null){
            return list1;
        }else if(list1.val >= list2.val){
            list2.next = mergeTwoLists(list1,list2.next);
            return list2;
            
        }else if(list1.val < list2.val){
            list1.next = mergeTwoLists(list1.next,list2);
            return list1;
        }
        return list1;

或者通过创建头节点进行遍历
遍历的同时，头节点 和l1 l2 的下一个位置移动
以及最后谁先结束 prev.next = l1 == null ? l2 : l1;
最后返回的值是头结点的下一个next

通过创建一个头节点，以及头指针遍历

关于怎么创建头节点的知识点可看我之前的文章
java中new ListNode(0)常见用法详细区别（全）

代码可能有的bug：

1. 创建临时节点prehead，最后要返回这个节点的next
2. list1==null?pre.next=list2:pre.next=list1;这种写法错误，要写成list1==null?pre.next=list2:list1;

class Solution {
    public ListNode mergeTwoLists(ListNode list1, ListNode list2) {
        // 创建头结点，一个用来存储值，一个用来遍历整个链表节点
        ListNode prehead = new ListNode(-1);
        ListNode pre = prehead;

        while(list1 != null && list2 != null){
            if(list1.val >= list2.val){
                pre.next = list2;
                list2 =list2.next;
            }else {
                pre.next = list1;
                list1 =list1.next;
            }
            // 公共的部分放在此处
            pre = pre.next;
        }

        // 合并后 l1 和 l2 最多只有一个还未被合并完，我们直接将链表末尾指向未合并完的链表即可
        pre.next = list1 == null ? list2:list1;
        return prehead.next;
    }
}

146. LRU 缓存（中等）**

请你设计并实现一个满足 LRU (最近最少使用) 缓存 约束的数据结构。
实现 LRUCache 类：
LRUCache(int capacity) 以 正整数 作为容量 capacity 初始化 LRU 缓存
int get(int key) 如果关键字 key 存在于缓存中，则返回关键字的值，否则返回 -1 。
void put(int key, int value) 如果关键字 key 已经存在，则变更其数据值 value ；如果不存在，则向缓存中插入该组 key-value 。如果插入操作导致关键字数量超过 capacity ，则应该 逐出 最久未使用的关键字。
函数 get 和 put 必须以 O(1) 的平均时间复杂度运行。

示例：

输入

[“LRUCache”, “put”, “put”, “get”, “put”, “get”, “put”, “get”, “get”, “get”]
[[2], [1, 1], [2, 2], [1], [3, 3], [2], [4, 4], [1], [3], [4]]
输出
[null, null, null, 1, null, -1, null, -1, 3, 4]
解释
LRUCache lRUCache = new LRUCache(2);
lRUCache.put(1, 1); // 缓存是 {1=1}
lRUCache.put(2, 2); // 缓存是 {1=1, 2=2}
lRUCache.get(1); // 返回 1
lRUCache.put(3, 3); // 该操作会使得关键字 2 作废，缓存是 {1=1, 3=3}
lRUCache.get(2); // 返回 -1 (未找到)
lRUCache.put(4, 4); // 该操作会使得关键字 1 作废，缓存是 {4=4, 3=3}
lRUCache.get(1); // 返回 -1 (未找到)
lRUCache.get(3); // 返回 3
lRUCache.get(4); // 返回 4

提示：

1 <= capacity <= 3000
0 <= key <= 10000
0 <= value <= 105
最多调用 2 * 105 次 get 和 put

思路

主要的思路是 通过哈希表加上双向链表
在java中有一个类也是这样，可以通过继承实现它来写
java之LinkedHashMap源码详细解析

public class LRUCache {
    class DLinkedNode {
        int key;
        int value;
        DLinkedNode prev;
        DLinkedNode next;
        public DLinkedNode() {}
        public DLinkedNode(int key, int value) {this.key = key; this.value = value;}
    }

    private Map<Integer, DLinkedNode> map = new HashMap<Integer, DLinkedNode>();
    private int size;
    private int capacity;
    private DLinkedNode head, tail;

    public LRUCache(int capacity) {
    // 注意此处的差异
        this.size = 0;
        this.capacity = capacity;
        // 使用伪头部和伪尾部节点
        head = new DLinkedNode();
        tail = new DLinkedNode();
        head.next = tail;
        tail.prev = head;
    }

 public int get(int key) {
        DLinkedNode node= map.get(key);
        if(node==null) return -1 ;
         // 如果 key 存在，先通过哈希表定位，再移到头部
        removeNode(node);
        addToHead(node);
        return node.value;
    }

    public void put(int key, int value) {
        DLinkedNode node=map.get(key);
        if(node == null){
         // 如果 key 不存在，创建一个新的节点
            DLinkedNode newnode=new DLinkedNode(key,value); 
             // 添加进哈希表
            map.put(key,newnode);  
            //添加头部 并且size加1
            addToHead(newnode);
            size++;
            if(size>capacity){
            //移除尾部，map删除
                DLinkedNode tail=removeTail();
                map.remove(tail.key);
                size--;
            }
        }
        else{
        // 如果 key 存在，先通过哈希表定位，再修改 value，并移到头部
            node.value = value;//不可省略
            removeNode(node);
            addToHead(node);
        }

      
    }

    private void addToHead(DLinkedNode node) {
        node.prev = head;
        node.next = head.next;
        head.next.prev = node;
        head.next = node;
    }

    private void removeNode(DLinkedNode node) {
        node.prev.next = node.next;
        node.next.prev = node.prev;
    }
    
    private DLinkedNode removeTail() {
        DLinkedNode res = tail.prev;
        removeNode(res);
        return res;
    }
}

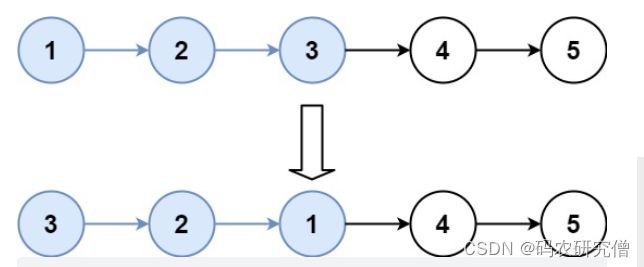
25. K 个一组翻转链表（困难）**

给你一个链表，每 k 个节点一组进行翻转，请你返回翻转后的链表。

k 是一个正整数，它的值小于或等于链表的长度。

如果节点总数不是 k 的整数倍，那么请将最后剩余的节点保持原有顺序。

进阶：

你可以设计一个只使用常数额外空间的算法来解决此问题吗？
你不能只是单纯的改变节点内部的值，而是需要实际进行节点交换。

示例 1：

输入：head = [1,2,3,4,5], k = 2
输出：[2,1,4,3,5]
示例 2：

输入：head = [1,2,3,4,5], k = 3
输出：[3,2,1,4,5]

示例 3：

输入：head = [1,2,3,4,5], k = 1
输出：[1,2,3,4,5]

示例 4：

输入：head = [1], k = 1
输出：[1]

提示：

列表中节点的数量在范围 sz 内
1 <= sz <= 5000
0 <= Node.val <= 1000
1 <= k <= sz

---

思路：

关于这篇文章的思路，主要结合反转链表的一部分
具体在于中间的衔接点怎么使用，以及k个，前后顺序的状态

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {
    public ListNode reverseKGroup(ListNode head, int k) {

        ListNode dummy=new ListNode(0);
        dummy.next=head;

        ListNode pre=dummy;
        ListNode end=dummy;
        

        while(end.next!=null){
            for(int i=0;i<k&&end!=null;i++){
                end=end.next;
            }
            if(end==null)break;
            ListNode next=end.next;
            end.next=null;
            ListNode start= pre.next;
            pre.next=reverse(start);
            start.next=next;
            pre=start;
            end=start;

        }
        return dummy.next; 

    }


    public ListNode reverse(ListNode rear){
        ListNode prev=null;
        ListNode rev=rear;
        while(rev!=null){
            ListNode next=rev.next;
            rev.next=prev;
            
            prev=rev;
            rev=next;
        }
        return prev;
    }

}

关于以上代码可看如下类似的注解解释：
或者看官方的解释，比较易懂
图解k个一组翻转链表的解释

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) { val = x; }
 * }
 */
class Solution {
    public ListNode reverseKGroup(ListNode head, int k) {
        if (head == null || head.next == null){
            return head;
        }
        //定义一个假的节点。
        ListNode dummy=new ListNode(0);
        //假节点的next指向head。
        // dummy->1->2->3->4->5
        dummy.next=head;
        //初始化pre和end都指向dummy。pre指每次要翻转的链表的头结点的上一个节点。end指每次要翻转的链表的尾节点
        ListNode pre=dummy;
        ListNode end=dummy;

        while(end.next!=null){
            //循环k次，找到需要翻转的链表的结尾,这里每次循环要判断end是否等于空,因为如果为空，end.next会报空指针异常。
            //dummy->1->2->3->4->5 若k为2，循环2次，end指向2
            for(int i=0;i<k&&end != null;i++){
                end=end.next;
            }
            //如果end==null，即需要翻转的链表的节点数小于k，不执行翻转。
            if(end==null){
                break;
            }
            //先记录下end.next,方便后面链接链表
            ListNode next=end.next;
            //然后断开链表
            end.next=null;
            //记录下要翻转链表的头节点
            ListNode start=pre.next;
            //翻转链表,pre.next指向翻转后的链表。1->2 变成2->1。 dummy->2->1
            pre.next=reverse(start);
            //翻转后头节点变到最后。通过.next把断开的链表重新链接。
            start.next=next;
            //将pre换成下次要翻转的链表的头结点的上一个节点。即start
            pre=start;
            //翻转结束，将end置为下次要翻转的链表的头结点的上一个节点。即start
            end=start;
        }
        return dummy.next;


    }
    //链表翻转
    // 例子：   head： 1->2->3->4
    public ListNode reverse(ListNode head) {
         //单链表为空或只有一个节点，直接返回原单链表
        if (head == null || head.next == null){
            return head;
        }
        //前一个节点指针
        ListNode preNode = null;
        //当前节点指针
        ListNode curNode = head;
        //下一个节点指针
        ListNode nextNode = null;
        while (curNode != null){
            nextNode = curNode.next;//nextNode 指向下一个节点,保存当前节点后面的链表。
            curNode.next=preNode;//将当前节点next域指向前一个节点   null<-1<-2<-3<-4
            preNode = curNode;//preNode 指针向后移动。preNode指向当前节点。
            curNode = nextNode;//curNode指针向后移动。下一个节点变成当前节点
        }
        return preNode;

    }


}

第二天

14. 最长公共前缀（简单）

题目：

编写一个函数来查找字符串数组中的最长公共前缀。

如果不存在公共前缀，返回空字符串 “”。

示例 1：

输入：strs = [“flower”,“flow”,“flight”]
输出：“fl”

示例 2：

输入：strs = [“dog”,“racecar”,“car”]
输出：“”
解释：输入不存在公共前缀。

提示：

1 <= strs.length <= 200
0 <= strs[i].length <= 200
strs[i] 仅由小写英文字母组成

---

思路：

通过对比所有的列，一列一列比较
终止条件有两个（通过两个for进行遍历，而且实时刻刻都是只有一个第一行的每一列进行比较strs[0].charAt(j）

• 这一列的长度等于其遍历的当前列的长度strs[i].length()==j
• 不同列的相同位置strs[i].charAt(j)!=strs[0].charAt(j)

如果执行完都不返回的话，最后就是本身，输出strs【0】即可

字符串数组，有两个区别，取全部的字符串长度，则为strs.length;，取单个数组内部的字符串则为strs[0].length()（容易弄混）

class Solution {
    public String longestCommonPrefix(String[] strs) {
        int m = strs.length;

        // 长度返回需要注意，此处为字符串的长度
        int n = strs[0].length();

        for(int j = 0;j < n;j++){
            // 不从1开始，自动把第一行作为基准进行比较
            for(int i = 1;i < m;i++){
                // 提前结束的条件，一个是判断结束，一个是不相等提前结束
                if(strs[i].length() == j || strs[i].charAt(j) != strs[0].charAt(j)){
                    // substring 而不是subString
                    return strs[0].substring(0,j);
                }        
            }
        }

        return strs[0];
    }
}

另外一种思路是，对比每一行的，一行一行的比较。最后输出其结果即可

class Solution {
    public String longestCommonPrefix(String[] strs) {
        int m = strs.length;
        String prefix = strs[0];

        for(int i = 1;i < m;i++){
            // strs[i].length() 此处为字符串的数组长度，为length()
            int length = Math.min(strs[i].length(),prefix.length());
        
            int j;
            // 此处的长度，为两者字符串的最小值
            for(j = 0;j < length;j++){
                if(strs[i].charAt(j) != prefix.charAt(j)){
                    break;
                }
            }

            //int index=0;
            //while(index
            //prefix=strs[i].substring(0,index);

            prefix = strs[i].substring(0,j);
        }

        return prefix;
    }
}

3. 无重复字符的最长子串（中等）

题目：

给定一个字符串 s ，请你找出其中不含有重复字符的 最长子串 的长度。

示例 1:

输入: s = “abcabcbb”
输出: 3
解释: 因为无重复字符的最长子串是 “abc”，所以其长度为 3。

示例 2:

输入: s = “bbbbb”
输出: 1
解释: 因为无重复字符的最长子串是 “b”，所以其长度为 1。

示例 3:

输入: s = “pwwkew”
输出: 3
解释: 因为无重复字符的最长子串是 “wke”，所以其长度为 3。
请注意，你的答案必须是 子串 的长度，“pwke” 是一个子序列，不是子串。

提示：

0 <= s.length <= 5 * 104
s 由英文字母、数字、符号和空格组成

---

思路：

通过遍历数组，为了减少一次遍历，可以通过set集合进行遍历
如果出现重复，则删除第一个节点，继续开始从第二个节点开始遍历（因为从第一个节点到查重重复 是不能算入子串的）
集合已经添加进入了，第二个指针可以不用挪到最开始的地方。

class Solution {
    public int lengthOfLongestSubstring(String s) {
     Set<Character>set=new HashSet<>();
     int n=s.length();
     int ans=0,rk=0;

     for(int i=0;i<n;i++){
         if(i!=0) set.remove(s.charAt(i-1));
         while(rk<n&&!set.contains(s.charAt(rk))){
             set.add(s.charAt(rk));
             rk++;
         }
        ans=Math.max(ans,rk-i);
     }
     return ans;
    }
}

以上是因为rk的节点，每次都会往右在挪一个节点位置，所以不用减1
如果rk节点要想减1，可以通过下面的代码设置

class Solution {
    public int lengthOfLongestSubstring(String s) {
        // 哈希集合，记录每个字符是否出现过
        Set<Character> occ = new HashSet<Character>();
        int n = s.length();
        // 右指针，初始值为 -1，相当于我们在字符串的左边界的左侧，还没有开始移动
        int rk = -1, ans = 0;
        for (int i = 0; i < n; ++i) {
            if (i != 0) {
                // 左指针向右移动一格，移除一个字符
                occ.remove(s.charAt(i - 1));
            }
            while (rk + 1 < n && !occ.contains(s.charAt(rk + 1))) {
                // 不断地移动右指针
                occ.add(s.charAt(rk + 1));
                ++rk;
            }
            // 第 i 到 rk 个字符是一个极长的无重复字符子串
            ans = Math.max(ans, rk - i + 1);
        }
        return ans;
    }
}

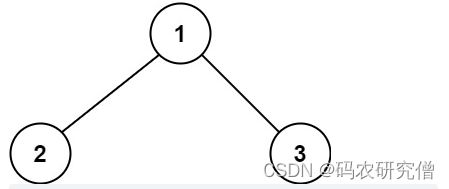
124. 二叉树中的最大路径和（困难）

题目：124. 二叉树中的最大路径和

路径 被定义为一条从树中任意节点出发，沿父节点-子节点连接，达到任意节点的序列。同一个节点在一条路径序列中 至多出现一次 。该路径 至少包含一个 节点，且不一定经过根节点。

路径和 是路径中各节点值的总和。

给你一个二叉树的根节点 root ，返回其 最大路径和 。

示例 1

输入：root = [1,2,3]
输出：6
解释：最优路径是 2 -> 1 -> 3 ，路径和为 2 + 1 + 3 = 6

示例 2

输入：root = [-10,9,20,null,null,15,7]
输出：42
解释：最优路径是 15 -> 20 -> 7 ，路径和为 15 + 20 + 7 = 42

提示：

树中节点数目范围是 [1, 3 * 10⁴]
-1000 <= Node.val <= 1000

class Solution {
    // 可以为负值，所以最大值设置为 Integer.MIN_VALUE
    int maxsum = Integer.MIN_VALUE;
    public int maxPathSum(TreeNode root) {
        maxGain(root);
        return maxsum;
    
    }
    public int maxGain(TreeNode node){
        // 递归的终止条件，如果没有终止条件无法递归
        if (node == null) {
            return 0;
        }

        // 自上而下的递归
        int leftGain = Math.max(maxGain(node.left),0);
        int rightGain = Math.max(maxGain(node.right),0);

        // 全局变量赋值求cur 的maxsum
        int cur = leftGain + rightGain + node.val;

        maxsum = Math.max(cur,maxsum);

        // 递归的返回值，一个节点不能同时走两个方向，求一个方向最大值即可
        return node.val + Math.max(leftGain,rightGain);
    }
}

第三天

206. 反转链表（简单）

给你单链表的头节点 head ，请你反转链表，并返回反转后的链表。

示例 1：

输入：head = [1,2,3,4,5]
输出：[5,4,3,2,1]

示例 2：

输入：head = [1,2]
输出：[2,1]

示例 3：

输入：head = []
输出：[]

提示：

链表中节点的数目范围是 [0, 5000]
-5000 <= Node.val <= 5000

---

1.思路一：
ListNode rear可以在任何时刻定义
也可直接使用ListNode rear=cur.next;
返回的是pre指针，而不是cur指针也不是head指针
具体的逻辑思路如下

class Solution {
    public ListNode reverseList(ListNode head) {
        // 定义三个指针，前中后
        ListNode cur = head,pre = null;
        ListNode rear = null;
        
        // 这种判断只需要 纠正一个方向即可，如果纠正两个方向，条件需要改变
        while(cur != null){
            
            rear = cur.next;
            cur.next = pre;

            pre = cur;
            cur = rear;
        }
        return pre;

    }
}

中途的错误做法：
只截取上面片段代码作为讲解：
将rear=cur.next;放在while里面最后定义，rear已经越界了

ListNode cur=head,pre=null;
ListNode rear;
 while(cur!=null){
            
            cur.next=pre;

            pre=cur;
            cur=rear;   
            rear=cur.next;   
        }
            

2.思路二：
使用递归的条件进行反转
递这个用法用在了层层递进
归这个用法用在了每一层的特殊情节，也就是两个链表地址空间的反转

class Solution {
    public ListNode reverseList(ListNode head) {
        // 终止条件，特别是head.next == null 这个 条件不可少
        if (head == null || head.next == null) {
            return head;
        }

        // 用head.next遍历递归，利用指针记住当前位置
        ListNode newhead = reverseList(head.next);

        // 遍历的交换
        head.next.next = head;
        head.next = null;
        return newhead;

    }
}

199. 二叉树的右视图（中等）

题目：

给定一个二叉树的 根节点 root，想象自己站在它的右侧，按照从顶部到底部的顺序，返回从右侧所能看到的节点值。

示例 1:

输入: [1,2,3,null,5,null,4]
输出: [1,3,4]

示例 2:

输入: [1,null,3]
输出: [1,3]

示例 3:

输入: []
输出: []

提示:

二叉树的节点个数的范围是 [0,100]
-100 <= Node.val <= 100

---

思路：

主要的思路是层次遍历的应用，在每一层的最后一个节点输出即可
对层次遍历熟悉就好操作

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public List<Integer> rightSideView(TreeNode root) {
        List<Integer> list = new ArrayList<>();
        if(root == null)return list;

        LinkedList<TreeNode> que = new LinkedList<>();
        que.offer(root);
        while(!que.isEmpty()){
            int n = que.size();
            for(int i = 0;i < n;i++){
                TreeNode node = que.poll();
                if(i == n - 1)list.add(node.val);
                if(node.left != null) que.offer(node.left);
                if(node.right != null) que.offer(node.right);
            }
        }
        return list;

    }
}

bytedance-016. 最短移动距离（简单）？？？

题目：bytedance-016. 最短移动距离

这道题没想出来
给出如下题目，如果有大佬想出来，可评论区留言

给定一棵 n 个节点树。节点 1 为树的根节点，对于所有其他节点 i，它们的父节点编号为 floor(i/2) (i 除以 2 的整数部分)。在每个节点 i 上有 a[i] 个房间。此外树上所有边均是边长为 1 的无向边。
树上一共有 m 只松鼠，第 j 只松鼠的初始位置为 b[j]，它们需要通过树边各自找到一个独立的房间。请为所有松鼠规划一个移动方案，使得所有松鼠的总移动距离最短。

格式：

输入：

• 输入共有三行。
• 第一行包含两个正整数 n 和 m，表示树的节点数和松鼠的个数。
• 第二行包含 n 个自然数，其中第 i 个数表示节点 i 的房间数 a[i]。
• 第三行包含 m 个正整数，其中第 j 个数表示松鼠 j 的初始位置 b[j]。
  输出：
• 输出一个数，表示 m 只松鼠各自找到独立房间的最短总移动距离。

示例：

输入：
5 4
0 0 4 1 1
5 4 2 2
输出：4
解释：前两只松鼠不需要移动，后两只松鼠需要经节点 1 移动到节点 3

提示：

对于 30% 的数据，满足 n,m <=100。
对于 50% 的数据，满足 n,m <=1000。
对于所有数据，满足 n,m<=100000，0<=a[i]<=m, 1<=b[j]<=n。

由于样例太少，给出两个反例：

31 2
1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 2 0 0 0 0
13 26

输出为3

63 2
0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0
1 13

输出为4

有想出来的大佬可评论留言

第四天

1. 两数之和（简单）

题目：

给定一个整数数组 nums 和一个整数目标值 target，请你在该数组中找出 和为目标值 target 的那 两个 整数，并返回它们的数组下标。

你可以假设每种输入只会对应一个答案。但是，数组中同一个元素在答案里不能重复出现。

你可以按任意顺序返回答案。

示例 1：

输入：nums = [2,7,11,15], target = 9
输出：[0,1]
解释：因为 nums[0] + nums[1] == 9 ，返回 [0, 1] 。

示例 2：

输入：nums = [3,2,4], target = 6
输出：[1,2]
示例 3：

输入：nums = [3,3], target = 6
输出：[0,1]

提示：

2 <= nums.length <= 10⁴
-10⁹ <= nums[i] <= 10⁹
-10⁹ <= target <= 10⁹
只会存在一个有效答案
进阶：你可以想出一个时间复杂度小于 O(n2) 的算法吗？

---

思路：
常规的思路可以使用暴力遍历，但是复杂度比较高
可以使用哈希表的存储进行存取

此处不可用set，因为返回的类型为下标值，所以用map最合适，可以通过map。get获取下标
通过target-nums【i】进行获取
而且map哈希中是containsKey，返回一个数组类型是new int[]{map.get(target-nums[i]),i};
如果为空值则为return new int[0];

class Solution {
    public int[] twoSum(int[] nums, int target) {
        int n = nums.length;
        Map<Integer,Integer> map = new HashMap<>();

        for(int i = 0;i < n;i++){
            // 对应如果只存在，则进行添加两个值
            if(map.containsKey(target - nums[i])){
                return new int[]{map.get(target - nums[i]),i};
            }
            map.put(nums[i],i);
        }

        // 返回初始数组的默认值
        return new int[0];
    }
}

15. 三数之和（中等）

题目：

给你一个包含 n 个整数的数组 nums，判断 nums 中是否存在三个元素 a，b，c ，使得 a + b + c = 0 ？请你找出所有和为 0 且不重复的三元组。

注意：答案中不可以包含重复的三元组。

示例 1：

输入：nums = [-1,0,1,2,-1,-4]
输出：[[-1,-1,2],[-1,0,1]]

示例 2：

输入：nums = []
输出：[]

示例 3：

输入：nums = [0]
输出：[]

提示：

0 <= nums.length <= 3000
-105 <= nums[i] <= 105

---

思路：

先排序，步步逼近双指针

最主要的条件是 去重而且一开始大于0都要去掉

通过判定总值 跟0的比较，移动指针的位置，使用while一直移动指针，而且最后还要前进一个，如果是L++ 最后要在进一个L。++L是最合适的。再者使用while的同时 一直不会跳出大循环，所以每个小循环都要L

列表中添加数组，主要通过这个函数进行转换：Arrays.asList() 详解
而且需要使用ArrayList而不是List这个函数

list.add(new ArrayList<Integer>(Arrays.asList(nums[i],nums[L],nums[R])));

关于这部分的解答 更详细的题解 可看如下链接：
三数之和（排序+双指针，易懂图解）
画解算法：15. 三数之和

class Solution {
    public List<List<Integer>> threeSum(int[] nums) {
        List<List<Integer>> list = new ArrayList<List<Integer>>();
        int n = nums.length;
        Arrays.sort(nums);

        // < nums.length - 2是为了保证后面还能存在两个数字
        for(int i = 0;i < n - 2;i++){
            //大于0，则后面的数字也是大于零（排序后是递增的）
            if(nums[i] > 0)break;
            // 代表第一个值重复了，去重
            if(i != 0 && nums[i] == nums[i - 1])continue;

            int left = i + 1;
            int right = n - 1;
            while(left < right){
                int sum = nums[i] + nums[left] + nums[right];
                if(sum == 0){
                    //创建一个空的列表

                    /*
                    Listsonlist=new ArrayList<>();
                    sonlist.add(nums[i]);
                    sonlist.add(nums[left]);
                    sonlist.add(nums[right]);
                    
                    list.add(sonlist);
                    */

                    list.add(new ArrayList<>(Arrays.asList(nums[i],nums[left],nums[right])));

                    // 以下都是为了去重
                    while(left < right && nums[left] == nums[++left]);
                    while(left < right && nums[right] == nums[--right]);
                
                }else if(sum < 0){
                    while(left < right && nums[left] == nums[++left]);
                }else if (sum > 0){
                    while(left < right && nums[right] == nums[--right]);
                }
            }
            
        }
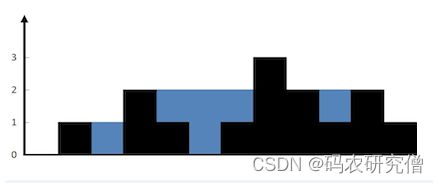
        return list;

    }
}

42. 接雨水（困难）*

题目：42. 接雨水

给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

示例 1：

输入：height = [0,1,0,2,1,0,1,3,2,1,2,1]
输出：6
解释：上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图，在这种情况下，可以接 6 个单位的雨水（蓝色部分表示雨水）。

示例 2：

输入：height = [4,2,0,3,2,5]
输出：9

提示：

n == height.length
1 <= n <= 2 * 10⁴
0 <= height[i] <= 10⁵

---

思路：

动态规划：（下雨后水能到达的最大高度等于下标 i两边的最大高度的最小值，下标 i处能接的雨水量等于下标 i 处的水能到达的最大高度减去 height[i]）

class Solution {
    public int trap(int[] height) {
        int n = height.length;

        // 定义左边界最大的值，注意边界范围
        int[] leftmax = new int[n];
        leftmax[0] = height[0];
        for(int i = 1;i < n;i++){
            leftmax[i] = Math.max(leftmax[i - 1],height[i]);
        }
        
        // 定义右边界最大的值，注意边界范围
        int[] rightmax = new int[n];
        rightmax[n - 1] = height[n - 1];
        for(int i = n - 2;i >= 0;i--){
            rightmax[i] = Math.max(rightmax[i + 1],height[i]);
        }

        // 两者最小的边界，减去height即为蓄水池
        int sum = 0;
        for(int i = 0;i < n;i++){
            sum += Math.min(leftmax[i],rightmax[i]) - height[i];
        }

        return sum;
    }
}

双指针：

class Solution {
    public int trap(int[] height) {
        int n = height.length;

        int left = 0;
        int right = n - 1;
        int leftmax = 0;
        int rightmax = 0;
        
        int sum = 0;
        // 边界条件是 left < right
        while(left < right){
            // 保持左右边界最大的值，维护两个值
            leftmax = Math.max(leftmax,height[left]);
            rightmax = Math.max(rightmax,height[right]);

            // 哪个边界小，就用这个边界 减去自身height的值
            if(height[left] < height[right]){
                sum += leftmax - height[left];
                left++;
            }else {
                sum += rightmax - height[right];
                right--;
            }
        }
        return sum;
    }
}

第五天

7. 整数反转（中等）

题目

给你一个 32 位的有符号整数 x ，返回将 x 中的数字部分反转后的结果。

如果反转后整数超过 32 位的有符号整数的范围 [−231, 231 − 1] ，就返回 0。

假设环境不允许存储 64 位整数（有符号或无符号）。

示例 1：

输入：x = 123
输出：321

示例 2：

输入：x = -123
输出：-321

示例 3：

输入：x = 120
输出：21

示例 4：

输入：x = 0
输出：0

提示：

-231 <= x <= 231 - 1

---

思路一：
这道题的思路很像之前那道算法

【leetcode】数学 - 回文数

但是有个前提条件，而且可以是负数
所以在要加以判断，否则会溢出

class Solution {
    public int reverse(int x) {
        int res = 0;
        while(x != 0){
			// 一定要除以10，因为1534236469的输入，输出是0，而不是本身 
			// 如果反转后整数超过 32 位的有符号整数的范围 [−231,  231 − 1] ，就返回 0
            if(res < Integer.MIN_VALUE / 10 || res > Integer.MAX_VALUE / 10){
                return 0;
            }
            int ret = x % 10;
            // 核心代码在这一步
            res = res * 10 + ret;

            x /= 10;
        }
        return res;

    }
}

215. 数组中的第K个最大元素（中等）

题目：

给定整数数组 nums 和整数 k，请返回数组中第 k 个最大的元素。

请注意，你需要找的是数组排序后的第 k 个最大的元素，而不是第 k 个不同的元素。

示例 1:

输入: [3,2,1,5,6,4] 和 k = 2
输出: 5

示例 2:

输入: [3,2,3,1,2,4,5,5,6] 和 k = 4
输出: 4

提示：

1 <= k <= nums.length <= 10⁴
-10⁴ <= nums[i] <= 10⁴

---

思路：

使用快排的思路将其遍历出来
具体快排的思路可看我这篇文章
【数据结构】常见排序算法详细分析（内含java与c++代码）

其快排代码思路如下：

class Solution {
    
    public int findKthLargest(int[] nums, int k) {
        quicksort(nums,0,nums.length-1);
        // 返回第k大的数组值
        return nums[nums.length-k];

    }

    // 使用快排的思想进行排序
    public void quicksort(int [] nums,int left,int right){
        // 边界条件 特别要注意
        if(left > right)return;

        int l = left;
        int r = right;

        // 以左边的第一个为基准
        int temp = nums[l];//基准的数字

        // 筛选出一个有序数字的位置
        while(l < r){
            while(l < r && nums[r] >= temp)r--;
            while(l < r && nums[l] <= temp)l++;
            if(l < r){
                int t = nums[l];
                nums[l] = nums[r];
                nums[r] = t;
            } 
        }

        //最后的基准 跟（i与j相等）i互换位置
        nums[left] = nums[l];
        nums[l] = temp;

        // 遍历递归左右边界的值
        quicksort(nums,left,l-1);
        quicksort(nums,l+1,right);
    }
}

也可使用堆的思想，本身优先队列就有堆的思想：（具体可看我以下文章）

• java中的PriorityQueue底层和实现原理深入源码探究
• 【数据结构】栈与队列区分push pop offer poll containsKey put等

class Solution {
    public int findKthLargest(int[] nums, int k) {

        // 使用优先队列，默认是小顶堆
        PriorityQueue <Integer> que = new PriorityQueue<>();
        for(int num :nums){
            que.add(num);
            if(que.size() > k){
                // 去除最小的，因为是小顶堆
                que.poll();
            }
            
        }
        // 返回堆顶就是 第k个最大的
        return que.peek();
    }
}

23. 合并K个升序链表（困难）*

题目：23. 合并K个升序链表

给你一个链表数组，每个链表都已经按升序排列。

请你将所有链表合并到一个升序链表中，返回合并后的链表。

示例 1：

输入：lists = [[1,4,5],[1,3,4],[2,6]]
输出：[1,1,2,3,4,4,5,6]
解释：链表数组如下：
[
1->4->5,
1->3->4,
2->6
]
将它们合并到一个有序链表中得到。
1->1->2->3->4->4->5->6

示例 2：

输入：lists = []
输出：[]

示例 3：

输入：lists = [[]]
输出：[]

提示：

k == lists.length
0 <= k <= 10⁴
0 <= lists[i].length <= 500
-10^4 <= lists[i][j] <= 10⁴
lists[i] 按 升序 排列
lists[i].length 的总和不超过 10⁴

用优先队列的思想

class Solution {
    public ListNode mergeKLists(ListNode[] lists) {

        // java lambda表达式新写法（ Comparator.comparingInt(o->o.vaal) ）
        PriorityQueue<ListNode>pq=new PriorityQueue<>(Comparator.comparingInt(o->o.val));
        
        int n=lists.length;
        // 只添加每个list的第一个节点
        for(int i=0;i<n;i++){
            if(lists[i]!=null) pq.offer(lists[i]);
           
        }

        // 创建头结点以及头指针
        ListNode head=new ListNode(-1);
        ListNode ans=head;

        // 优先队列不为空，进入条件
        while(!pq.isEmpty()){
            // 将其出栈，通过头指针指向该节点，并且挪到头指针
            ListNode cur=pq.poll();
            ans.next=cur;
            ans=ans.next;

            // 判断该list 下一个的next是否为空，添加下个节点
            if(cur.next!=null){
                pq.offer(cur.next);
            }
        }

        // 返回头结点的next
        return head.next;


    }
}

第六天

33. 搜索旋转排序数组（中等）*

题目：

整数数组 nums 按升序排列，数组中的值 互不相同 。

在传递给函数之前，nums 在预先未知的某个下标 k（0 <= k < nums.length）上进行了 旋转，使数组变为 [nums[k], nums[k+1], …, nums[n-1], nums[0], nums[1], …, nums[k-1]]（下标 从 0 开始 计数）。例如， [0,1,2,4,5,6,7] 在下标 3 处经旋转后可能变为 [4,5,6,7,0,1,2] 。

给你 旋转后 的数组 nums 和一个整数 target ，如果 nums 中存在这个目标值 target ，则返回它的下标，否则返回 -1 。

示例 1：

输入：nums = [4,5,6,7,0,1,2], target = 0
输出：4

示例 2：

输入：nums = [4,5,6,7,0,1,2], target = 3
输出：-1

示例 3：

输入：nums = [1], target = 0
输出：-1

提示：

1 <= nums.length <= 5000
-10⁴<= nums[i] <= 10⁴
nums 中的每个值都 独一无二
题目数据保证 nums 在预先未知的某个下标上进行了旋转
-10⁴ <= target <= 10⁴

进阶：你可以设计一个时间复杂度为 O(log n) 的解决方案吗？

---

思路：

采用二分查找的方法

将数组一分为二，其中一定有一个是有序的，另一个可能是有序，也能是部分有序。
此时有序部分用二分法查找。无序部分再一分为二，其中一个一定有序，另一个可能有序，可能无序。就这样循环.

关于该题解看的是如下提示：
官方题解

class Solution {
    public int search(int[] nums, int target) {
        // 处理边界问题
        int n = nums.length;
        int l = 0;
        int r = n - 1;

        // 总体大条件为 l 小于等于r
        while(l <= r){
            // 求出mid
            int mid = l + (r - l) / 2;
            if(nums[mid] == target)return mid;

            // 主要分两种大情况，nums【mid】的值和第一个进行比较，查看是否落在哪个位置
            if(nums[0] <= nums[mid]){
                // 如果归于左边，则左边的target具体位置 判断落的地点在哪，好处理边界
                if(nums[0] <= target && target < nums[mid]){
                    r = mid - 1;
                }else {
                    l = mid + 1;
                }
            }else {
                // 注意等于号的位置
                if(nums[mid] < target && target <= nums[n - 1]){
                    l = mid + 1;
                }else {
                    r = mid - 1;
                }
            }
        }
        return -1;
    }
}

54. 螺旋矩阵（中等）

题目：

给你一个 m 行 n 列的矩阵 matrix ，请按照 顺时针螺旋顺序 ，返回矩阵中的所有元素。

示例 1：

输入：matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出：[1,2,3,6,9,8,7,4,5]

示例 2：

输入：matrix = [[1,2,3,4],[5,6,7,8],[9,10,11,12]]
输出：[1,2,3,4,8,12,11,10,9,5,6,7]

提示：

m == matrix.length

n == matrix[i].length
1 <= m, n <= 10
-100 <= matrix[i][j] <= 100

---

思路：

一个循环一个循环的输出，同时要在每个循环中加一个判断，随时计数器结束就停止循环，不然会出现下方某个错误

class Solution {
    public List<Integer> spiralOrder(int[][] matrix) {
        // 以下算法为模拟算法

        int m =matrix.length;
        int n = matrix[0].length;
        List<Integer> list = new ArrayList<>();
        
        // 定义四个边界值
        int l = 0;
        int r = n - 1;
        int top = 0;
        int bottom = m - 1 ;

        // 通过计数判断
        int num = 1;
        int sum = m * n;
        while(num <= sum){
            // 定义的是n - 1，所以有等于号，在内部的遍历随时可能结束，所以要带上num <= sum 的条件

            // 遍历注意起始条件
            for(int i = l;i <= r && num <= sum;i++){
                list.add(matrix[top][i]);
                num++;
            }
            top++;//往下加1

            for(int i = top;i <= bottom && num <= sum;i++){
                list.add(matrix[i][r]);
                num++;
            }
            r--;//往左减1

            // ----注意遍历的i 是减减 ---
            for(int i = r;i >= l && num <= sum;i--){
                list.add(matrix[bottom][i]);
                num++;
            }
            bottom--;//往上加1

            for(int i = bottom;i >= top && num <= sum;i--){
                list.add(matrix[i][l]);
                num++;
            }
            l++;//往右加1
        }
        return list;
    }
}

每个条件中要加入&&num<=sum，否则一个while出不了循环，特别是长方形会有错误

示例拓展：
59. 螺旋矩阵 II

class Solution {
    public int[][] generateMatrix(int n) {

        int [][] ss = new int[n][n];
        
        // 定义四个边界值
        int l = 0;
        int r = n - 1;
        int top = 0;
        int bottom = n - 1 ;

        // 通过计数判断
        int num = 1;
        int sum = n * n;

        while(num <= sum){
            for(int i = l;i <= r;i++){
                ss[top][i] = num++;
            }
            top++;//往下走

            for(int i = top;i <= bottom;i++){
                ss[i][r] = num++;
            }
            r--;//往左走

            for(int i = r;i >= l;i--){
                ss[bottom][i] = num++;
            }
            bottom--;//往上走

            for(int i = bottom;i >= top;i--){
                ss[i][l] = num++;
            }
            l++;//往右走
        }
        return ss;

    }
}

bytedance-006. 夏季特惠（简单）**

题目：bytedance-006. 夏季特惠

某公司游戏平台的夏季特惠开始了，你决定入手一些游戏。现在你一共有X元的预算，该平台上所有的 n 个游戏均有折扣，标号为 i 的游戏的原价 ai元，现价只要 bi 元（也就是说该游戏可以优惠 ai - bi元）并且你购买该游戏能获得快乐值为 wi。由于优惠的存在，你可能做出一些冲动消费导致最终买游戏的总费用超过预算，但只要满足获得的总优惠金额不低于超过预算的总金额，那在心理上就不会觉得吃亏。现在你希望在心理上不觉得吃亏的前提下，获得尽可能多的快乐值。

格式：

输入：

• 第一行包含两个数 n 和 X 。
• 接下来 n 行包含每个游戏的信息，原价 ai,现价 bi，能获得的快乐值为 wi 。
  输出：
• 输出一个数字，表示你能获得的最大快乐值。

示例 1：

输入：
4 100
100 73 60
100 89 35
30 21 30
10 8 10
输出：100
解释：买 1、3、4 三款游戏，获得总优惠 38 元，总金额 102 元超预算 2 元，满足条件，获得 100 快乐值。

示例 2：

输入：
3 100
100 100 60
80 80 35
21 21 30
输出：60
解释：只能买下第一个游戏，获得 60 的快乐值。

示例 3：

输入：
2 100
100 30 35
140 140 100
输出：135
解释：两款游戏都买，第一款游戏获得优惠 70 元，总开销 170 元，超过预算 70 元，超出预算金额不大于获得优惠金额满足条件，因此可以获得最大快乐值为 135。

提示：

所有输入均为整型数
1 <= n <= 500
0 <= x <= 10,000
0 <= b_i <= a_i <= 500
1 <= w_i <= 1,000,000,000
关于数据集：
前 30% 的数据， 小数据集 (n<=15)
中间 30% 的数据，中等数据集 (n<=100)
后 40% 的数据，大数据集 (n<=500)

import java.util.*;

class Main {
    public static void main(String[] args) {
        // 1. 输入数据
        Scanner sc = new Scanner(System.in);

        int n = sc.nextInt();
        int X = sc.nextInt();

        int[] a = new int[n];
        int[] b = new int[n];
        int[] w = new int[n];

        // 2. 去除重量 <= 0 物品 
        int num = 0;
        long base = 0;
        for (int i = 0; i < n; i++) {
            a[num] = sc.nextInt();
            b[num] = sc.nextInt();
            w[num] = sc.nextInt();
            // 总优惠金额不低于超过预算的总金额 通过b【num】与0进行比较
            b[num] = b[num] - (a[num] - b[num]); // 作为物品重量
            if (b[num] <= 0) {
                X += -b[num];
                base += w[num];
            } else {
                num++;
            }
        }

        // 3. 对剩余物品进行01背包求解
        long[] dp = new long[X + 1];
        for (int i = 0; i < num; i++) {
            for (int j = X; j >= b[i]; j--) {
                dp[j] = Math.max(dp[j], dp[j - b[i]] + w[i]);
            }
        }
        System.out.println(dp[X] + base); // 任何容量的背包都可以直接加上重量<=0 的物品的价值和
    }
}

第七天

53. 最大子数组和（中等）

题目：
给你一个整数数组 nums ，请你找出一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。

子数组 是数组中的一个连续部分。

示例 1：

输入：nums = [-2,1,-3,4,-1,2,1,-5,4]
输出：6
解释：连续子数组 [4,-1,2,1] 的和最大，为 6 。

示例 2：

输入：nums = [1]
输出：1

示例 3：

输入：nums = [5,4,-1,7,8]
输出：23

提示：

1 <= nums.length <= 105
-104 <= nums[i] <= 104

进阶：如果你已经实现复杂度为 O(n) 的解法，尝试使用更为精妙的 分治法 求解。

---

具体思路如下：
通过Math函数，将其一个个加上获取最大值
以及通过Math函数，存储各个区域中的最大子数组之和

通过动态规划的思路进行滚动数组

class Solution {
    public int maxSubArray(int[] nums) {
        int n = nums.length;

        // 最大的前缀值
        int pre = 0;
        // 遍历所有，所有值最大的一个，赋值为nums【0】，如果数组只有一个，则返回nums【0】
        int max = nums[0];
        for(int i = 0;i < n;i++){
            pre = Math.max(pre+nums[i],nums[i]);
            // 所有的遍历都筛选出最大的max
            max = Math.max(pre,max);
        }
        return max;
    }
}

152. 乘积最大子数组（中等）

题目：

给你一个整数数组 nums ，请你找出数组中乘积最大的非空连续子数组（该子数组中至少包含一个数字），并返回该子数组所对应的乘积。

测试用例的答案是一个 32-位 整数。

子数组 是数组的连续子序列。

示例 1:

输入: nums = [2,3,-2,4]
输出: 6
解释: 子数组 [2,3] 有最大乘积 6。

示例 2:

输入: nums = [-2,0,-1]
输出: 0
解释: 结果不能为 2, 因为 [-2,-1] 不是子数组。

提示:

1 <= nums.length <= 2 * 10⁴
-10 <= nums[i] <= 10
nums 的任何前缀或后缀的乘积都 保证 是一个 32-位 整数

---

因为可能为负数，所以要保存最大值和最小值。再者，定义的总数一开始就不应该为0，而是Integer.MIN_VALUE
如果下一个数为负数，则最大值和最小值互换

具体代码如下：

class Solution {
    public int maxProduct(int[] nums) {
        int n = nums.length;

        int max = 1;
        int min = 1;
        // 此处定义的sum 初始不应为0，如果只有一个nums，并且为负数，那么最大就会为0
        int sum = Integer.MIN_VALUE;
        for(int i = 0;i < n;i++){
            // 先判断nums小于0再进行判断
            if(nums[i] < 0){
                int temp = max;
                max = min;
                min = temp;
            }
            max=Math.max(nums[i]*max,nums[i]);
            min=Math.min(nums[i]*min,nums[i]);

            sum=Math.max(sum,max);
        }
        return sum;
    }
}

41. 缺失的第一个正数（困难）

题目：41. 缺失的第一个正数

给你一个未排序的整数数组 nums ，请你找出其中没有出现的最小的正整数。

请你实现时间复杂度为 O(n) 并且只使用常数级别额外空间的解决方案。

示例 1：

输入：nums = [1,2,0]
输出：3

示例 2：

输入：nums = [3,4,-1,1]
输出：2

示例 3：

输入：nums = [7,8,9,11,12]
输出：1

提示：

1 <= nums.length <= 5 * 10⁵
-2³¹ <= nums[i] <= 2³¹ - 1

原地置换的思想：

class Solution {
    public int firstMissingPositive(int[] nums) {
        int n = nums.length;
        // 数组的原地置换，精髓在于 nums[nums[i] - 1]  ，nums[i] 这两个交换
        for(int i = 0;i < n;i++){
            // 一直再这交换，前提的条件要大于0 小于n 
            while(nums[i] > 0 && nums[i] < n && nums[nums[i] - 1] != nums[i]){
                int temp = nums[nums[i] - 1];
                nums[nums[i] - 1] = nums[i];
                nums[i] = temp;
            }
        }

        // 如果不相等，直接返回i + 1
        for(int i = 0;i < n;i++){
            if(nums[i] != i + 1){
                return i + 1;
            }
        }
        // 返回最大的元素
        return n + 1;
    }
}

还有一种思路是哈希表：

• 将其小于等于0的，变为n+1
• 小于等于n的 ，nums[num - 1] = -Math.abs(nums[num - 1]);变为负数
• 返回第一个大于0下标元素 + 1

class Solution {
    public int firstMissingPositive(int[] nums) {
        int n = nums.length;
        for (int i = 0; i < n; ++i) {
            if (nums[i] <= 0) {
                nums[i] = n + 1;
            }
        }
        // 最主要的核心
        for (int i = 0; i < n; ++i) {
            int num = Math.abs(nums[i]);
            if (num <= n) {
                nums[num - 1] = -Math.abs(nums[num - 1]);
            }
        }
        for (int i = 0; i < n; ++i) {
            if (nums[i] > 0) {
                return i + 1;
            }
        }
        return n + 1;
    }
}

第八天

20. 有效的括号（简单）

题目：

给定一个只包括 ‘(’，‘)’，‘{’，‘}’，‘[’，‘]’ 的字符串 s ，判断字符串是否有效。

有效字符串需满足：

左括号必须用相同类型的右括号闭合。
左括号必须以正确的顺序闭合。

示例 1：

输入：s = “()”
输出：true

示例 2：

输入：s = “()[]{}”
输出：true

示例 3：

输入：s = “(]”
输出：false

示例 4：

输入：s = “([)]”
输出：false

示例 5：

输入：s = “{[]}”
输出：true

提示：

1 <= s.length <= 10⁴
s 仅由括号 ‘()[]{}’ 组成

---

思路：

注意一个代码格式：

Map <Character,Character> map=new HashMap<>(){{
            put(')','('); 
            }} ;

通过哈希表存储其键值对
通过栈的形式防其值

• 如果值没有包括进去，则进栈
• 如果值包括了进去，则要出栈的话（需要判断其键值是否满足栈顶元素以及栈是否为空，因为可能为 ((）,不想此处判断栈是否为空的话，可以在一开始就判断是否为偶数个数）
• 单纯的进栈还不可以，因为要键值配对，必须把栈清空，所以最后的栈必须为空，示例如下
  
  代码如下：

class Solution {
    public boolean isValid(String s) {
        if(s.length()%2==1)return false;
        Deque <Character>stack=new LinkedList<>();
        Map <Character,Character> map=new HashMap<>(){{
            put(')','(');
            put('}','{');
            put(']','[');
        }};

        for(char c:s.toCharArray()){
            if(map.containsKey(c)){
                if(map.get(c)!=stack.peek()){                   
                    return false;
                }
                stack.pop(); 
            }else {
                stack.push(c);
            }
            
        }
        return stack.isEmpty();

    }
}

不使用map集合：

class Solution {
    public boolean isValid(String s) {
         // 不使用map结构，直接进行比较
        Deque<Character> stack = new LinkedList<>();
        for(int i = 0; i < s.length();i++){
            // 单个字符 无法使用equals进行比较判断
            if(s.charAt(i) == '('){
                stack.push(')');
            }else if(s.charAt(i) == '{'){
                stack.push('}');
            }else if(s.charAt(i) == '['){
                stack.push(']');
                // 如果栈为空，或者对应的peek 不相等，则直接返回false
            }else if (stack.isEmpty() ||  stack.peek() != s.charAt(i) ){
                return false;
            }else {
                // 右边的括号配对成功，就会将其右括号出栈
                stack.pop();
            }
        }

        return stack.isEmpty();
    }
}

200. 岛屿数量（中等）

题目：

给你一个由 ‘1’（陆地）和 ‘0’（水）组成的的二维网格，请你计算网格中岛屿的数量。

岛屿总是被水包围，并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。

此外，你可以假设该网格的四条边均被水包围。

示例 1：

输入：grid = [
[“1”,“1”,“1”,“1”,“0”],
[“1”,“1”,“0”,“1”,“0”],
[“1”,“1”,“0”,“0”,“0”],
[“0”,“0”,“0”,“0”,“0”]
]
输出：1

示例 2：

输入：grid = [
[“1”,“1”,“0”,“0”,“0”],
[“1”,“1”,“0”,“0”,“0”],
[“0”,“0”,“1”,“0”,“0”],
[“0”,“0”,“0”,“1”,“1”]
]
输出：3

提示：

m == grid.length

n == grid[i].length
1 <= m, n <= 300
grid[i][j] 的值为 ‘0’ 或 ‘1’

---

思路：

通过深度优先遍历，将其遍历过后的数字都变为一个0，也就是状态变量
如果一开始进入的为1，则sum+1
在遍历的时候终止条件，一般有临界值，以及状态值

class Solution {
    public int numIslands(char[][] grid) {
        if(grid == null || grid.length == 0)return 0;

        int m = grid.length;
        int n = grid[0].length;

        int sum = 0;
        for(int i = 0;i < m;i++){
            for(int j = 0;j < n;j++){
                if(grid[i][j] == '1'){
                    sum++;
                    dfs(grid,i,j);
                }
            }
        }
        return sum;
    }

    public void dfs(char[][] grid,int i,int j){
        int m = grid.length;
        int n = grid[0].length;

        // 临界条件不满足的return 返回
        
        // grid[i][j] == '0' 这个条件需要放在后面，先处理越界问题
        if(i < 0 || i >= m || j < 0 || j >= n || grid[i][j] == '0' ){
            return;
        }

        // 更改原数组，将其赋值为0
        grid[i][j] = '0';
        dfs(grid,i - 1,j);
        dfs(grid,i + 1,j);
        dfs(grid,i,j - 1);
        dfs(grid,i,j + 1);
    }
}

上面的思路是修改了原数组，如果不想修改原数组，增加一个状态变量的数组，具体代码如下：（核心代码如下）

class Solution {
    public int numIslands(char[][] grid) {
        if(grid == null || grid.length == 0)return 0;

        int m = grid.length;
        int n = grid[0].length;

        // 默认一开始的初始值为0
        int[][] visited = new int[m][n];
        int sum = 0;
        for(int i = 0;i < m;i++){
            for(int j = 0;j < n;j++){
                if(grid[i][j] == '1' && visited[i][j] != 1){
                    sum++;
                    dfs(grid,i,j,visited);
                }
            }
        }
        return sum;
    }

    public void dfs(char[][] grid,int i,int j,int[][] visited){
        int m = grid.length;
        int n = grid[0].length;

        // 临界条件不满足的return 返回

        // grid[i][j] == '0' 这个条件需要放在后面，先处理越界问题
        if(i < 0 || i >= m || j < 0 || j >= n || grid[i][j] == '0' || visited[i][j] == 1){
            return;
        }

        // 更改原数组，将其赋值为0
        visited[i][j] = 1;
        dfs(grid,i - 1,j,visited);
        dfs(grid,i + 1,j,visited);
        dfs(grid,i,j - 1,visited);
        dfs(grid,i,j + 1,visited);
    }
}

76. 最小覆盖子串（困难）******

题目：76. 最小覆盖子串

给你一个字符串 s 、一个字符串 t 。返回 s 中涵盖 t 所有字符的最小子串。如果 s 中不存在涵盖 t 所有字符的子串，则返回空字符串 “” 。

注意：

对于 t 中重复字符，我们寻找的子字符串中该字符数量必须不少于 t 中该字符数量。
如果 s 中存在这样的子串，我们保证它是唯一的答案。

示例 1：

输入：s = “ADOBECODEBANC”, t = “ABC”
输出：“BANC”

示例 2：

输入：s = “a”, t = “a”
输出：“a”

示例 3:

输入: s = “a”, t = “aa”
输出: “”
解释: t 中两个字符 ‘a’ 均应包含在 s 的子串中，
因此没有符合条件的子字符串，返回空字符串。

提示：

1 <= s.length, t.length <= 10⁵
s 和 t 由英文字母组成

进阶：你能设计一个在 o(n) 时间内解决此问题的算法吗？

---

这道题没啥思路，用的是官方题解：

class Solution {
    Map<Character, Integer> ori = new HashMap<Character, Integer>();
    Map<Character, Integer> cnt = new HashMap<Character, Integer>();

    public String minWindow(String s, String t) {
        int tLen = t.length();
        for (int i = 0; i < tLen; i++) {
            char c = t.charAt(i);
            ori.put(c, ori.getOrDefault(c, 0) + 1);
        }
        int l = 0, r = -1;
        int len = Integer.MAX_VALUE, ansL = -1, ansR = -1;
        int sLen = s.length();
        while (r < sLen) {
            ++r;
            if (r < sLen && ori.containsKey(s.charAt(r))) {
                cnt.put(s.charAt(r), cnt.getOrDefault(s.charAt(r), 0) + 1);
            }
            while (check() && l <= r) {
                if (r - l + 1 < len) {
                    len = r - l + 1;
                    ansL = l;
                    ansR = l + len;
                }
                if (ori.containsKey(s.charAt(l))) {
                    cnt.put(s.charAt(l), cnt.getOrDefault(s.charAt(l), 0) - 1);
                }
                ++l;
            }
        }
        return ansL == -1 ? "" : s.substring(ansL, ansR);
    }

    public boolean check() {
        Iterator iter = ori.entrySet().iterator(); 
        while (iter.hasNext()) { 
            Map.Entry entry = (Map.Entry) iter.next(); 
            Character key = (Character) entry.getKey(); 
            Integer val = (Integer) entry.getValue(); 
            if (cnt.getOrDefault(key, 0) < val) {
                return false;
            }
        } 
        return true;
    }
}

第九天

105. 从前序与中序遍历序列构造二叉树（中等）**

题目：

给定两个整数数组 preorder 和 inorder ，其中 preorder 是二叉树的先序遍历， inorder 是同一棵树的中序遍历，请构造二叉树并返回其根节点。

示例 1:

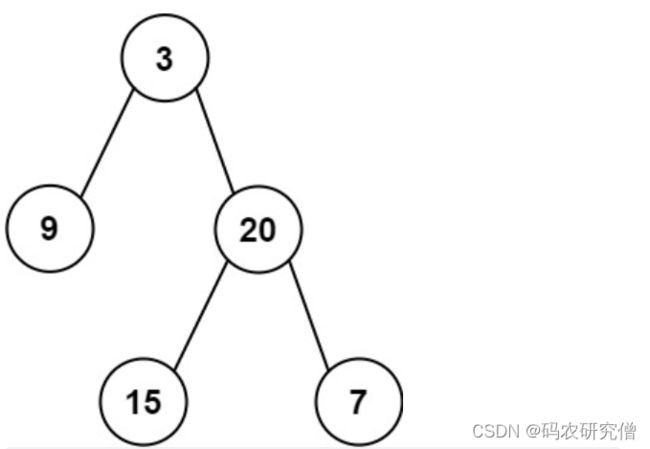
输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
输出: [3,9,20,null,null,15,7]
示例 2:

输入: preorder = [-1], inorder = [-1]
输出: [-1]

提示:

1 <= preorder.length <= 3000
inorder.length == preorder.length
-3000 <= preorder[i], inorder[i] <= 3000
preorder 和 inorder 均 无重复 元素
inorder 均出现在 preorder
preorder 保证 为二叉树的前序遍历序列
inorder 保证 为二叉树的中序遍历序列

---

思路一：

使用递归的思路，因为先序遍历的第一个头节点是关键，因为他是根节点，与中序遍历的根节点相同，中序遍历的左子树，以及右子树就可区分，以此类推，就可找到其构建的二叉树

• 新建一个二叉树，要先创建一个根节点（找到中序遍历的根节点，然后一个个创建），通过TreeNode root=new TreeNode(preorder[preorder_left]);
• 每次都要先序遍历的根节点，在遍历中序遍历找到其根节点，复杂度变高了，可以通过set集合存储key value值
• 注意递归的终止条件是先序遍历，只要前面的节点大于后面的节点，输出为null
• 另外一个注意事项是，先序遍历和后序遍历的长度大小是一样的

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    Map<Integer,Integer>map;
    public TreeNode buildTree(int[] preorder, int[] inorder) {

        map=new HashMap<>();
        int n=inorder.length;
        for(int i=0;i<n;i++){
            map.put(inorder[i],i);
        }
        return mybuildTree(preorder,inorder,0,n-1,0,n-1);    

    }
    public TreeNode mybuildTree(int []preorder,int [] inorder,int preorder_left,int preorder_right,int inorder_left,int inorder_right ){
    // 通过判定前序的 left 指针大于 right指针
        if(preorder_left>preorder_right)return null;

        int inorder_root=map.get(preorder[preorder_left]);
        int sum=inorder_root-inorder_left;
        
        TreeNode root=new TreeNode(preorder[preorder_left]);
        root.left=mybuildTree(preorder,inorder,preorder_left+1,preorder_left+sum, inorder_left,inorder_root-1);
        root.right=mybuildTree(preorder,inorder,preorder_left+sum+1,preorder_right, inorder_root+1,inorder_right);
        return root;
    }
}

103. 二叉树的锯齿形层序遍历（中等）

题目：

给你二叉树的根节点 root ，返回其节点值的 锯齿形层序遍历 。（即先从左往右，再从右往左进行下一层遍历，以此类推，层与层之间交替进行）。

示例 1：

输入：root = [3,9,20,null,null,15,7]
输出：[[3],[20,9],[15,7]]

示例 2：

输入：root = [1]
输出：[[1]]

示例 3：

输入：root = []
输出：[]

提示：

树中节点数目在范围 [0, 2000] 内
-100 <= Node.val <= 100

---

思路：

通过层次遍历，在内部的列表中使用的是双端队列，如果存储1 23 的时候，通过存放为1 32.因为是双端队列，32 存放的时候是通过offerFirst进行存储
因为是双端队列，所以在添加的时候要强转list.add(new LinkedList(sonlist));

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public List<List<Integer>> zigzagLevelOrder(TreeNode root) {
        List<List<Integer>> list=new ArrayList<List<Integer>>();
        if(root==null)return list;
        

        Queue<TreeNode> que =new LinkedList<>();
        que.offer(root);
        boolean direction = true;
        while(!que.isEmpty()){
            Deque<Integer> sonlist=new LinkedList<>();
            int n=que.size();
            
            for(int i=0;i<n;i++){
                TreeNode node=que.poll();
                if(direction){
                    sonlist.offerLast(node.val);
                }else{
                    sonlist.offerFirst(node.val);
                }
                if(node.left!=null)que.offer(node.left);
                if(node.right!=null)que.offer(node.right);
            }

            direction=!direction;
            list.add(new LinkedList<Integer>(sonlist));
            
        }

        return list;

    }
}

另一种思路是不使用双端队列
直接使用列表的形式进行添加
特殊行使用Collection进行反转

class Solution {
    public List<List<Integer>> zigzagLevelOrder(TreeNode root) {
        List<List<Integer>> list = new ArrayList<List<Integer>>();
        if(root == null)return list;

        Deque<TreeNode> que = new LinkedList<>();
        que.offer(root);
        boolean direction = true;
        while(!que.isEmpty()){
            List<Integer> sonlist = new ArrayList<>();
            int n = que.size();
            for(int i = 0;i < n;i++){
                TreeNode node = que.poll();
                sonlist.add(node.val);
                if(node.left != null)que.offer(node.left);
                if(node.right != null)que.offer(node.right);
            }
            if(!direction){
                Collections.reverse(sonlist);
            }
            direction = !direction;
            list.add(sonlist);

        }
        return list;
    }
}

bytedance-010. 数组组成最大数（简单）

题目：bytedance-010. 数组组成最大数

自定义排序

给定一组非负整数，重新排列它们的顺序使之组成一个最大的整数。

示例 1：

输入：[10,1,2]
输出：2110

示例 2：

输入：[3,30,34,5,9]
输出：9534330

import java.util.*;
public class Main{
    public static void main(String[] args){
        Scanner sc = new Scanner(System.in);
        String s = sc.nextLine();
        String[] nums = s.substring(1,s.length() - 1).split(",");

        // 第一种写法：lambda 表达式
        // Arrays.sort(nums,(a,b) -> (b + a).compareTo(a + b));

        // 改写Comparator钟的compare的方法，compareTO
        Arrays.sort(nums,new Comparator<String>(){
            @Override
            public int compare(String a,String b){
                return (b + a).compareTo(a + b);
            }
        });


        StringBuilder sb = new StringBuilder();
        for(String num : nums){
            sb.append(num);
        }
        System.out.println(sb.toString());
    }
}

第十天

94. 二叉树的中序遍历（简单）

题目：

给定一个二叉树的根节点 root ，返回它的 中序 遍历。

示例 1：

输入：root = [1,null,2,3]
输出：[1,3,2]

示例 2：

输入：root = []
输出：[]

示例 3：

输入：root = [1]
输出：[1]

示例 4：

输入：root = [1,2]
输出：[2,1]

示例 5：

提示：

树中节点数目在范围 [0, 100] 内
-100 <= Node.val <= 100

进阶: 递归算法很简单，你可以通过迭代算法完成吗？

---

思路一：
通过递归 的方式
创建一个函数，将其res列表传入

class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> list = new ArrayList<>();
        // 调用函数
        inorder(root,list);
        return list;
    }

    // 中序遍历的递归，前中后，如果为null则直接return
    public void inorder(TreeNode root,List<Integer> res){
        if(root == null){
            return ;
        }
        inorder(root.left,res);
        res.add(root.val);
        inorder(root.right,res);
    }
}

思路二：

通过迭代的方式进行
利用栈的思想

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> list = new ArrayList<>();
        Stack<TreeNode> stack = new Stack<>();

        // 两个条件，root不为空 或者 栈不为空
        while(root != null ||!stack.isEmpty()){
            // 对应的所有左子树先入栈
            while(root != null){
                stack.push(root);
                root = root.left;
            }
           
            // 添加栈中元素
            root = stack.pop();
            list.add(root.val);
            // 遍历是否有右子树
            root = root.right;
        }
        return list;
    }
}

102. 二叉树的层序遍历（中等）

题目：

给你二叉树的根节点 root ，返回其节点值的 层序遍历 。 （即逐层地，从左到右访问所有节点）。

示例 1：

输入：root = [3,9,20,null,null,15,7]
输出：[[3],[9,20],[15,7]]

示例 2：

输入：root = [1]
输出：[[1]]

示例 3：

输入：root = []
输出：[]

提示：

树中节点数目在范围 [0, 2000] 内
-1000 <= Node.val <= 1000

---

思路：

通过列表以及队列的方式进行存储

具体大条件是判断其队列不为空
内部存储的是每一层的列表size
注意泛型的类型

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public List<List<Integer>> levelOrder(TreeNode root) {
        List<List<Integer>> list = new ArrayList<List<Integer>>();
        if(root == null)return list;

        // 定义队列的格式
        Queue<TreeNode> que = new LinkedList<>();
        que.offer(root);
        while(!que.isEmpty()){
            // 定义子列表
            List<Integer> sonlist = new ArrayList<>();
            int n = que.size();
            for(int i = 0;i < n;i++){
                TreeNode node = que.poll();
                // poll的时候将其add进入
                sonlist.add(node.val);
                if(node.left != null)que.offer(node.left);
                if(node.right != null)que.offer(node.right);
            }
            list.add(sonlist);
        }
        return list;
    }
    
}

394. 字符串解码（中等）

题目：

给定一个经过编码的字符串，返回它解码后的字符串。

编码规则为: k[encoded_string]，表示其中方括号内部的 encoded_string 正好重复 k 次。注意 k 保证为正整数。

你可以认为输入字符串总是有效的；输入字符串中没有额外的空格，且输入的方括号总是符合格式要求的。

此外，你可以认为原始数据不包含数字，所有的数字只表示重复的次数 k ，例如不会出现像 3a 或 2[4] 的输入。

示例 1：

输入：s = “3[a]2[bc]”
输出：“aaabcbc”

示例 2：

输入：s = “3[a2[c]]”
输出：“accaccacc”

示例 3：

输入：s = “2[abc]3[cd]ef”
输出：“abcabccdcdcdef”

示例 4：

输入：s = “abc3[cd]xyz”
输出：“abccdcdcdxyz”

提示：

• 1 <= s.length <= 30
• s 由小写英文字母、数字和方括号 ‘[]’ 组成
• s 保证是一个 有效 的输入。
• s 中所有整数的取值范围为 [1, 300]

---

思路：

通过栈的存储，以及StringBulider的存储
遇到】的时候都进栈

错误代码展示

class Solution {
public String decodeString(String s) {
        
        Stack<Character>stack=new Stack<>();

        StringBuilder res=new StringBuilder();
        for(char c:s.toCharArray()){
            if(c!=']'){
                stack.push(c);
            }else{
                StringBuilder ans=new StringBuilder();
                while(!stack.isEmpty()&&Character.isLetter(stack.peek()))
                    ans.insert(0,stack.pop());
                String sub=ans.toString();

                stack.pop();

                ans = new StringBuilder();
                while(!stack.isEmpty()&&Character.isDigit(stack.peek()))
                    ans.insert(0,stack.pop());
                
                int count=Integer.valueOf(ans.toString());


                while(count>0){
                    for(char h:sub.toCharArray()){
                        res.append(h);                       
                    }
                    count--;
                }

            }

        }
        return res.toString();

    }
}

少考虑了这种情况：

对此在前面的时候不着急直接输出添加进去
而是继续放到栈中，等全部放到栈中之后在一一添加进去

正确代码如下：

• 判断是否为字符Character.isLetter(stack.peek()
• 或者是否为数字Character.isDigit(stack.peek()
• 将其栈从后往前的输出，可以通过insert 无限插入到第0个位置ans.insert(0,stack.pop());
• 字符串转换为数字Integer.valueOf();
• SrtingBuilder 输出的结构都要通过toString();先转换为字符串

class Solution {
    public String decodeString(String s) {
        Deque<Character> stack = new LinkedList<>();

        StringBuilder sb = new StringBuilder();
        for(char c : s.toCharArray()){
            if(c != ']'){
                // 不是这个括号的都进栈
                stack.push(c);
            }else {
                // 找出对应的所有字母，从后往前弹出找
                StringBuilder ans = new StringBuilder();
                while(!stack.isEmpty() && Character.isLetter(stack.peek())){
                    ans.insert(0,stack.pop());
                }
                // 放入sub字符串中
                String sub = ans.toString();

                // 弹出一个括号
                stack.pop();

                // 在找出它的数字
                StringBuilder res = new StringBuilder();
                while(!stack.isEmpty() && Character.isDigit(stack.peek())){
                    res.insert(0,stack.pop());
                }
                int count = Integer.valueOf(res.toString());


                // 将其字母重新放入栈中 （以倍数）
                while(count > 0){
                    for(char h : sub.toCharArray()){
                        stack.push(h);
                    }
                    count--;
                }
            }
        }

        // 将其栈按照原先进入的顺序 通过insert从前往后插入
        while(!stack.isEmpty()){
            sb.insert(0,stack.pop());
        }
        return sb.toString();
    }
}

第十一天

415. 字符串相加（简单）

题目：

给定两个字符串形式的非负整数 num1 和num2 ，计算它们的和并同样以字符串形式返回。

你不能使用任何內建的用于处理大整数的库（比如 BigInteger）， 也不能直接将输入的字符串转换为整数形式。

示例 1：

输入：num1 = “11”, num2 = “123”
输出：“134”

示例 2：

输入：num1 = “456”, num2 = “77”
输出：“533”

示例 3：

输入：num1 = “0”, num2 = “0”
输出：“0”

提示：

1 <= num1.length, num2.length <= 10⁴
num1 和num2 都只包含数字 0-9
num1 和num2 都不包含任何前导零

---

思路：

通过模拟的思路，将其两个字符串从后往前加上，如果有进位就保留进位

通过StringBuilder添加进入，但是记得要reverse反转，之后还要将其输出为字符串toString();

class Solution {
    public String addStrings(String num1, String num2) {
        // 临界值要计算，所以要减1
        int i = num1.length() - 1;
        int j = num2.length() - 1;
        int add = 0;

        StringBuilder sb = new StringBuilder();
        while(i >= 0 || j >= 0 || add != 0){
            // 在while 大条件下循环，如果小于0则直接返回0
            int x = i >= 0 ? num1.charAt(i) - '0': 0;
            int y = j >= 0 ? num2.charAt(j) - '0': 0;
            int result = add + x + y;
            sb.append(result % 10);
            add = result / 10;
            i--;
            j--;
        }
        // 最后要反转
        sb.reverse();
        return sb.toString();
    }
}

5. 最长回文子串（中等）**

题目：5. 最长回文子串

给你一个字符串 s，找到 s 中最长的回文子串。

示例 1：

输入：s = “babad”
输出：“bab”
解释：“aba” 同样是符合题意的答案。

示例 2：

输入：s = “cbbd”
输出：“bb”

提示：

1 <= s.length <= 1000
s 仅由数字和英文字母组成

中心拓展思路：

class Solution {
    public String longestPalindrome(String s) {
        if (s == null || s.length() < 1) {
            return "";
        }

        int start = 0,end = 0;
        for(int i = 0;i < s.length();i++){
            int len1 = expandAroundCenter(s,i,i);
            int len2 = expandAroundCenter(s,i,i + 1);
            int len = Math.max(len1,len2);
            if(len > end - start){
                // 之所以是len - 1，是处理奇数边界问题
                start = i - (len - 1) / 2;
                end = i + len / 2;
            }

        }
        // 左闭右开，所以要end + 1
        return s.substring(start,end + 1);
    }

    public int expandAroundCenter(String s, int left, int right) {
        while (left >= 0 && right < s.length() && s.charAt(left) == s.charAt(right)) {
            --left;
            ++right;
        }
        // 如果不匹配了
        // 此处的left以及right是在匹配元素边界：left 【匹配元素】 right
        // 因此回文串长度为：【left + 1，right - 1】，right - 1 - （left + 1）+ 1 = right - left - 1
        return right - left - 1;
    }
}

72. 编辑距离（困难）**

题目：72. 编辑距离

给你两个单词 word1 和 word2， 请返回将 word1 转换成 word2 所使用的最少操作数 。

你可以对一个单词进行如下三种操作：

插入一个字符
删除一个字符
替换一个字符

示例 1：

输入：word1 = “horse”, word2 = “ros”
输出：3
解释：
horse -> rorse (将 ‘h’ 替换为 ‘r’)
rorse -> rose (删除 ‘r’)
rose -> ros (删除 ‘e’)

示例 2：

输入：word1 = “intention”, word2 = “execution”
输出：5
解释：
intention -> inention (删除 ‘t’)
inention -> enention (将 ‘i’ 替换为 ‘e’)
enention -> exention (将 ‘n’ 替换为 ‘x’)
exention -> exection (将 ‘n’ 替换为 ‘c’)
exection -> execution (插入 ‘u’)

提示：

0 <= word1.length, word2.length <= 500
word1 和 word2 由小写英文字母组成

class Solution {
    public int minDistance(String word1, String word2) {
        int m = word1.length();
        int n = word2.length();

        int[][] dp = new int[m + 1][n + 1];
        dp[0][0] = 0;
        // word1删除元素，每删除一个，初始化都是下标删除的个数
        for(int i = 1;i < m + 1;i++){
            dp[i][0] = i;
        }

        for(int j = 1;j < n + 1;j++){
            dp[0][j] = j;
        }

        for(int i = 1;i < m + 1;i++){
            for(int j = 1;j < n + 1;j++){
                //如果配对，则保存上一个的值
                if(word1.charAt(i - 1) == word2.charAt(j - 1)){
                    dp[i][j] = dp[i - 1][j - 1];
                }else {
                    //如果不配对要分三种情况，第一种是word1删除，第二种是word2删除，第三种是两者都删除。三者之间比较出最小值，记得每删除一个元素都是要加1
                    dp[i][j] = Math.min(dp[i - 1][j - 1], Math.min(dp[i - 1][j],dp[i][j - 1])) + 1;
                }
                
            }
        }

        return dp[m][n];
    }
}