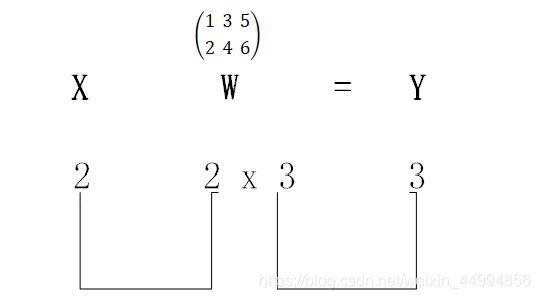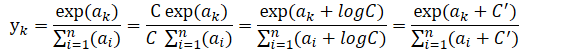第三章 神经网络

3.1从感知机到神经网络

3.1.1神经网络的例子

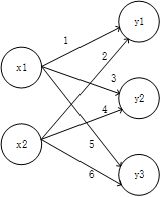
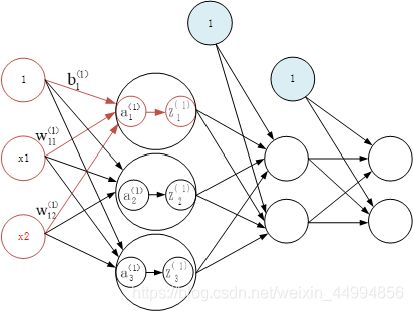
神经网络用图来表示：

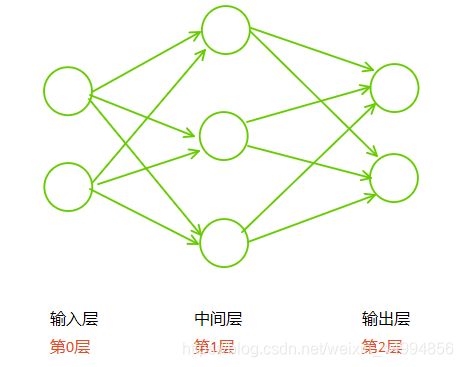
中间层有时也称为“隐藏层”。“隐藏”一词的意思是，隐藏层的神经元（和输入层、输出层不同），肉眼看不到
Tips ：上图网络中一共有三层神经元构成，但实际上只有两层神经元有权重，因此成为“2层网络”。本书将根据实质上拥有的权重层数（输入层，隐藏层，输出层的总数减去1后的数量）来表示网络的名称。

3.1.2复习感知机

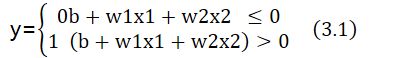
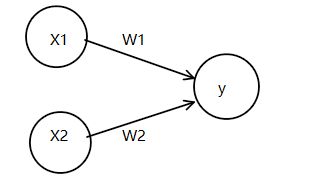
其中b被成为偏置的参数，用于控制神经元被激活的难易程度，w1和w2是表示各个信号的权重参数，用于控制各个信号的重要性。

在上图的网络中，偏置b并没有被画出来，如果要明确表示出来 ，可以添加权重为b的输出信号1，这个感知机将x1，x2，1作为神经元的输入，将其和各自的权重相乘后，传送至下一个神经元，在下一个神经元中，计算这些加权信号的总和。如果总和超过0，则输出1，否则输出0。

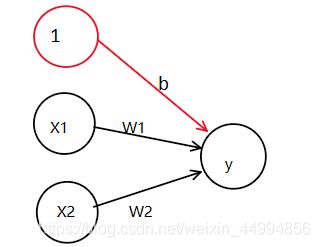
可以将3.1的式子改写为y=h(b+w1x1+w2x2) （式3.2），其中令a=(b+w1x1+w2x2)，y就可以表示为：

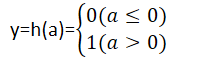
3.1.3激活函数登场

上面的h(x)函数会将输入信号的总和转换为输出信号，这种函数一般称为激活函数（activation function），激活函数的作用在于如何来激活输入信号的总和。


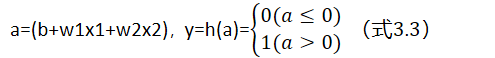
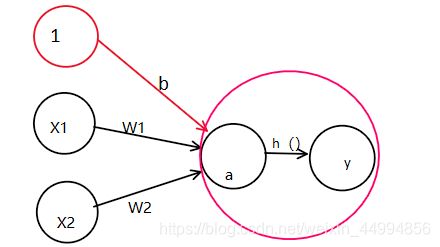
Tips:“朴素感知机”是指单层网络，指的是激活函数使用了阶跃函数的模型。阶跃函数是指一旦超过阈值，就切换输出函数。“多层感知机”是指神经网络，即使用sigmoid函数等平滑的激活函数的多层网络。

3.2激活函数

式（3.3）中的激活函数以阈值为界限，一旦输入的加权和超过阈值，就切换输出，这样的函数称为“阶跃函数”。因此可以说感知机中使用了阶跃函数作为激活函数。

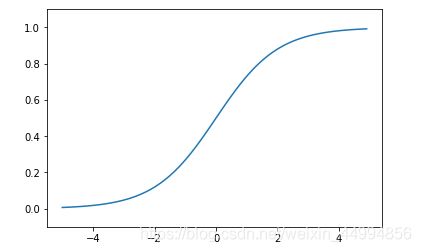
3.2.1sigmoid函数

神经网络中经常使用的一个激活函数就是sigmoid函数（sigmoid function）

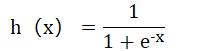
神经网络中用sigmoid函数作为激活函数，进行信号额转换，转换后的信号传给下一个神经元。感知机和神经网络的主要区别就在于这个激活函数。其他方面比如神经元的多层链接构造、信号的传递方法等基本上和感知机是一样的。

3.2.2阶跃函数的实现

阶跃函数

def step_function(x): #参数x只能接受实数（浮点数），但不允许取numpy数组
    if x>0:
        return 1
    else:
        return 0

允许参数为数组的阶跃函数

import numpy as np
def step_function(x):
    y=x>0
    return y,y.astype(np.int)#强制类型 转换

tips：可以用astype（）方法转换Numpy数组类型。astype（）方法通过参数指定期望的类型，这个例子是np.int型号，python中将布尔型转换为int型后，true会转换为1，false会转换为0。

3.2.3 阶跃函数的图形

import numpy as np
import matplotlib.pylab as plt
def step_function(x):
    return np.array(x>0,dtype=np.int)
x=np.arange(-5,5,0.1)
y=step_function(x)
plt.plot(x,y)
plt.ylim(-0.1,1.1)#指定y轴的范围
plt.show()

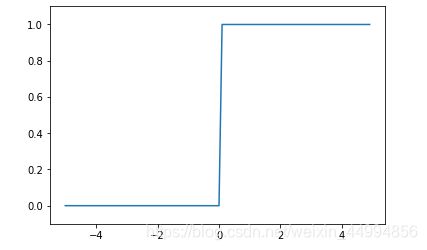
阶跃函数以0为界限，输出从0切换1，或者从1切换0，它的值呈阶梯型变化，所以称为阶跃函数。

3.2.4 sigmoid函数的实现

import numpy as np
def sigmoid(x):
    return 1/(1+np.exp(-x))

sigmoid函数图像

import matplotlib.pylab as plt
x=np.arange(-5,5,0.1)
y=sigmoid(x)
plt.plot(x,y)
plt.ylim(-0.1,1.1)#指定y轴的范围
plt.show()

3.2.5 sigmoid函数和阶跃函数的对比

x=np.arange(-5,5,0.1)
y1=sigmoid(x)
y2=step_function(x)
plt.plot(x,y1,label="sigmoid")
plt.plot(x,y2,linestyle="--",label="阶跃函数")
plt.xlabel("x")#设置x轴的标签
plt.ylabel("y")#设置x轴的标签
plt.legend()#给图像加上图例，具体用法参考：https://blog.csdn.net/qq_37710333/article/details/108308155
plt.ylim(-0.1,1.1)#指定y轴的范围
plt.show()

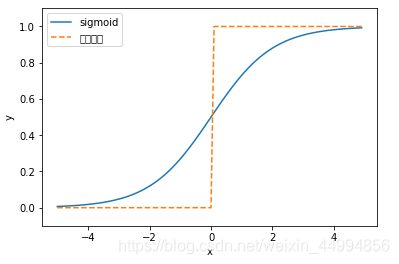
区别1：平滑性的不同。sigmoid函数是一条平滑的曲线，输出随着输入的变化连续变化。而阶跃信号以0为界限，输出发生急剧性变化。sigmoid函数的平滑性对神经网络的学习具有重要意义。
区别2：阶跃函数只能返回0和1，sigmoid函数能返回0到1之间的任意实数。也就是说感知机中神经元流动的是0或1的二元信号，而神经网络中流动的是连续的实数值信号。
共同性1：从宏观角度看，两个函数具有相似的形状。两者的结构均为“输入小时，输出接近于0，随着输入的增大，输出向1靠近”。也就是说，当输入信号为重要信息时，阶跃函数和sigmoid函数都会输出较大的值。当输入信号为不重要的信息时，两者都输出较小的值。
共同性2：不管输入信号有多小，或者有多大，输出信号的值都在0和1之间。

3.2.6 非线性函数（♥）

阶跃函数和sigmoid函数都是非线性函数。
神经网络的激活函数必须使用非线性函数。换句话说，激活函数不能使用线性函数。因为使用线性函数的话加深神经网络的层数就没有意义了。
线性函数的问题在于，不管如何加深层数，总存在与之等效的“无隐藏层的神经网络”

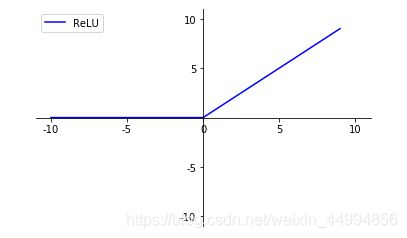
3.2.7 ReLU函数

sigmoid函数在很早就已经被使用了，最近则主要使用ReLU（Rectified Linear Unit）函数
ReLU函数在输入大于0时，直接输出该值；在输入小于等于0时，输出0。

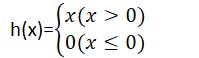
def ReLU(x):
    if x>0:
        return x
    else:
        return 0
#或者
def ReLU(x):
     return np.maxinum(0,x)

3.3多维数组的运算

3.3.1多维数组

简单的讲，多维数组就是"数字的集合"，数字排成一列的集合，排成长方形的集合，排成三维状或者N维状的集合都称为多维数组。
一维数组

数组的维数可以通过np.ndim()函数获得。
数组的形状可以通过实例变量shape获得。

二维数组

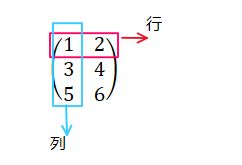
这里生成了一个3X2的数组B。3X2数组表示第一维度有三个元素，第二维度有两个元素。另外第一维度对应第0维，第二个维度对应第一维（Python的索引从0开始）

3.3.2矩阵乘法

矩阵相乘

Np.dot()接收两个numpy数组作为参数，并返回数组的乘积。
tips：要注意的是，np.dot(A,B)和np.dot(B,A)的值可能会不一样。和一般的运算（+或者*等）不同，矩阵的乘积中，操作数的顺序不同，结果也可能不同。

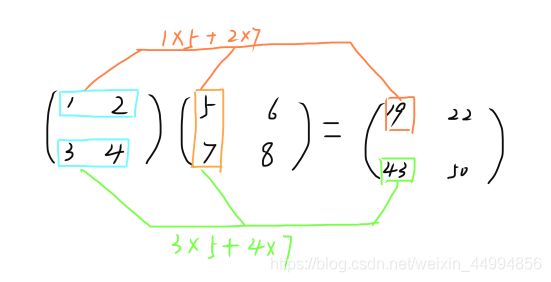
也可实现2X3的矩阵和3X2的矩阵的乘积，但不能实现如2X3矩阵和2X2矩阵的乘积，会出现错误。
具体来讲，两个矩阵相乘，矩阵A的第一维的元素个数（列数）必须和矩阵B的第0维的元素个数（行数）相等。

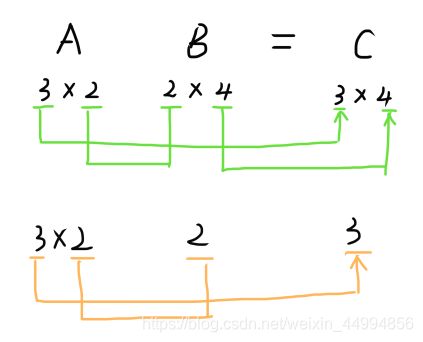
3.3.3神经网络的内积

import numpy as np
X=np.array([1,2])
W=np.array([[1,2,3],[4,5,6]])
Y=np.dot(X,W)
print(Y)

Tips：使用np.dot（多维数组的点积），可以一次性计算出Y的结果。这意味着即便Y的元素个数为100或者1000，也可以通过一次运就计算出结果！如果不使用np.dot，就必须单独计算Y的每一个元素（或者说必须使用for语句）。

3.4 三层神经网络的实现

以3层神经网络为对象，实现从输入到输出的（前向）处理。

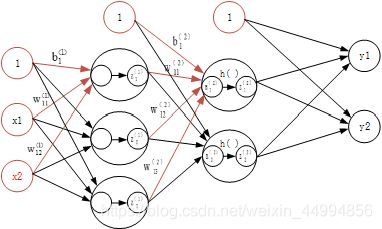
3层神经网络：输入层（第0层）有两个神经元，第一个隐藏层（第1层）有3个神经元，第二个隐藏层（第2层）有两个神经元，输出层（第三层）有2个神经元。

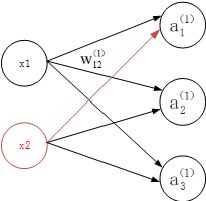
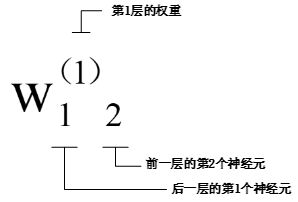
3.4.1符号确认

本节的重点是神经网络的运算可以作为矩阵运算打包进行。

3.4.2各层间信号传递的实现

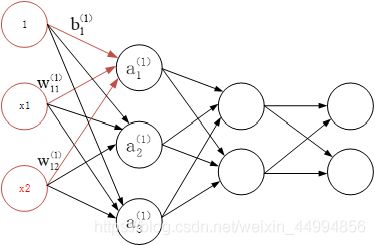
图中增加了偏置的神经元“1”。但是偏置的右下角的索引号只有一个。这是因为前一层的偏置神经元（神经元“1"）只有一个。

此外如果使用矩阵的乘法运算，则可以将第一层的加权和表示成下面的式子：

下面使用numpy数组来实现上面的式子，这里将输入信号、权重、偏置设为任意值。
从输入层向第1层传播

import numpy as np
X=np.array([0.1,0.2])
W1=np.array([[0.1,0.2,0.3],[0.4,0.5,0.6]])
B1=np.array([0.1,0.1,0.2])
A1=np.dot(X,W1)+B1
print(Y)
Z1=sigmoid(A1)
print(Z1)

第1层向第2层传播

W2=np.array([[0.1,0.2],[0.3,0.4],[0.2,0.6]])
B2=np.array([0.4,0.5])
A2=np.dot(A1,W2)+B2
print(A2)
Z2=sigmoid(A2)
print(Z2)

第2层向输出层传播

W3=np.array([[0.4,0.6],[0.2,0.3]])
B3=np.array([0.6,0.3])
A3=np.dot(Z2,W3)+B3
print(A3)
Z3=sigmoid(A3)
print(Z3)

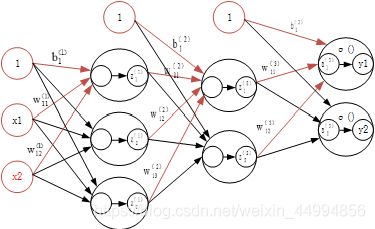
tips：输出层所用的激活函数，要根据求解问题的性质决定。
一般的：回归问题可以使用恒等函数，二元分类问题可以使用sigmoid函数，多分类问题可以使用softmax函数。

3.5输出层的设计

神经网络可以用在分类问题和回归问题上，不过需要根据实际情况改变输出层的激活函数。一般而言：回归问题用恒等函数，分类问题用softmax函数。
分类问题是数据属于哪一类的问题，比如分辨图片上是猫还是狗；而回归问题是根据某个输入预测一个（连续数值的问题），比如根据人的图像来预测体重

3.5.1恒等函数和softmax函数

恒等函数会将输入按照原样输出，对于输入的信息，不加任何改变的将其输出。因此在输出层使用恒等函数时，输入信号会原封不动地被输出。恒等函数进行转换处理可以用一根箭头来表示。
恒等函数

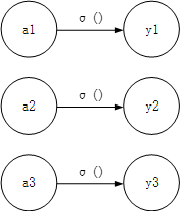
分类问题使用的softmax函数可以用下面的式子表示


softmax函数

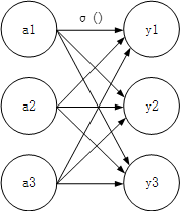
用上图表示softmax函数，softmax函数的输出通过箭头与所有的输入信号相连，这是因为输出层的各个神经元都受到所有输入信号的影响。

3.5.2实现softmax函数时的注意事项

import numpy as np
import matplotlib.pylab as plt
%matplotlib
def softmax(a):
    exp_a=np.exp(a)
    sum_exp_a=np.sum(exp_a)
    y=exp_a/sum_exp_a
    return y
a=np.arange(-5,10.1)
y=softmax(a)
plt.plot(a,y)
plt.ylim(0,0.3)#指定y轴的范围
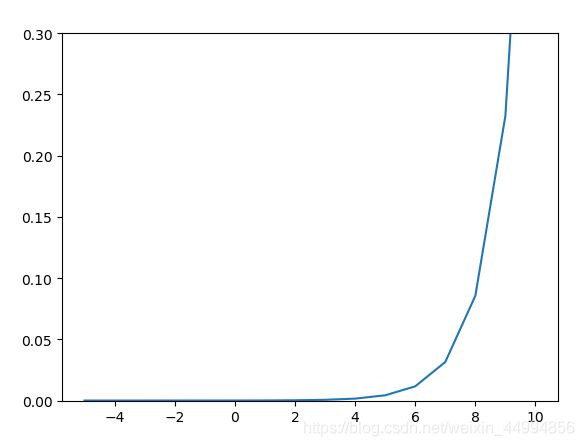
plt.show()

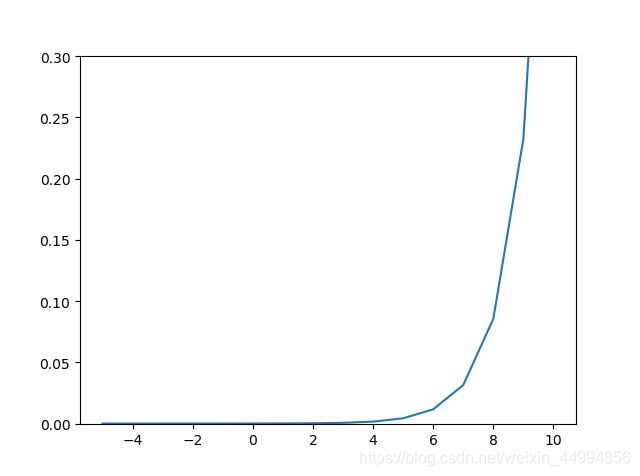
如图可见softmax函数虽然正确描述了式（3.10），但在计算机的运算过程中存在一定的缺陷，这个缺陷就是溢出问题：softmax函数的实现过程中要进行指数的运算，指数函数的值很容易变得很大。如果这些超大值进行除法运算，结果会出现“不确定”的情况。
tips：计算机在处理“数”时，数值必须在4字节或者8字节的有限数据宽度内，这就意味着数存在 有效位数，也就是说可以表示数值的范围是有限的，因此会出现超大值无法表示的问题。这个问题称为溢出问题。

import numpy as np
a=np.array([1010,1000,900])
exp_a=np.exp(a)
sum_exp_a=np.sum(exp_a)
y1=exp_a/sum_exp_a
c=np.max(a)
print(c)
exp_a1=np.exp(a-c)
sum_exp_a1=np.sum(np.exp(a-c))
y2=exp_a1/sum_exp_a1
print(y1)
print(y2)

def new_softmax(a):
    c=np.max(a)
    exp_a=np.exp(a-c)
    sum_exp_a=np.sum(np.exp(a-c))
    y=exp_a/sum_exp_a
    return y
a=np.arange(-5,10.1)
y=new_softmax(a)
plt.plot(a,y)
plt.ylim(0,0.3)#指定y轴的范围
plt.show()

3.5.3softmax函数的特征

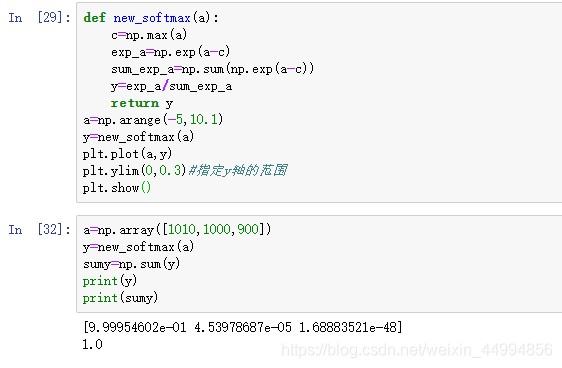
softmax函数输出的值是0.0到1.0之间的实数。并且softmax输出值的总和是1。正因为输出总和是1的这个性质，才可以把softmax函数的输出解释为“概率”。也就是说使用softmax函数，就可以用概率（统计）的方法处理问题。

一般而言，神经网络只把输出值最大的神经元所对应的类别作为识别结果，即便使用softmax函数，输出值最大值的神经元的位置 也不会改变，因为softmax函数是指数函数，是单调递增的。因此神经网络在进行分类时，输出层的softmax函数可以省略。

3.5.4 输出层的神经元数量

输出层的神经元数量一般根据待解决的问题来确定。对于分类问题，输出层的数量一般设定为类别的数量。比如手写数字识别（0-9），是个十分类问题，就可以将输出层的数量设为10个。

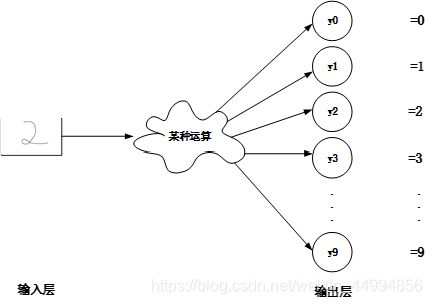
3.6手写数字识别（前向传播）

实现神经网络的推理也叫做前向传播（forward propagation）

和求解机器学习问题过程一样，也分为学习和推理两个过程。使用神经网络解决问题时，也需要首先使用训练数据（学习数据）进行权重参数学习，其次通过训练的模型对未知数据进行推理。

3.6.1 MNIST数据集

MNIST数据集是手写数字识别数据集，由0-9的手写数字构成，训练图像有6万张，预测图像有1万张。MNIST数据集的使用方法是：先用训练数据进行学习，再用学习到的模型度量能在多大程度上对测试图像进行正确的分类。

import sys,os
sys.path.append(os.pardir)
from mnist import load_mnist
(x_train,t_train),(x_test,t_test)=load_mnist(flatten=True,normalize=False,one_hot_label=False)
#第一个参数normalize设置是否将输入的图像正规化为0-1的值。如果设置为False，则图像的像素会保持原来的0-255
#第二个参数flatten设置是否展开输入图像（变成一维数组，如果将参数设置为False，则输入图像为1x28x28的三维数组；如果设置为true，则图像会保存为有784个元素构成的一维数组）
#第三个参数one_hot_label设置是否将标签保存为one-hot表示。
print(x_train.shape)
print(t_train.shape)
print(x_test.shape)
print(t_test.shape)

python有pickle这个便利的功能。这个功能可以将程序运行中的对象保存为文件。如果加载保存过的pickle文件，可以立刻复原之前程序运行中的对象。用于读入MNIST数据集的load _mnist()函数内部也使用了pickle功能（在第二次及 以后读入时）利用pickle功能可以高效的完成MNIST数据的准备工作。

import sys,os
import numpy as np
from PIL import Image
sys.path.append(os.pardir)
from mnist import load_mnist
defimg_show(img):
pil_img=Image.fromarray(np.uint8(img))
pil_img.show()
(x_train,t_train),(x_test,t_test)=load_mnist(flatten=True,normalize=False,one_hot_label=False)
img=x_train[0]
label=t_train[0]
print(label)
print(img.shape)
img=img.reshape(28,28)
print(img.shape)
img_show(img)

3.6.2 神经网络的推理处理

对MNIST数据集实现神经网络的推理处理。神经网络的输入层有784个神经元，输出层有10个神经元。输入层的784来源于图像的大小28x28，输出层的10来源于10类别分类（0-9）。此外，该神经网络有两个隐藏层，第一个隐藏层有50个神经元，第二个隐藏层有100个神经元（这里的50，100可以设置为任意值）

import sys,os
import pickle
import numpy as np
from PIL import Image
sys.path.append(os.pardir)
from mnist import load_mnist
 
defsigmoid(x):#定义sigmoid函数
return1/(1+np.exp(-x))
 
defsoftmax(a):#定义softmax函数
c=np.max(a)
exp_a=np.exp(a-c)
sum_exp_a=np.sum(np.exp(a-c))
y=exp_a/sum_exp_a
returny
 
defget_data():#定义读取数据的函数
(x_train,t_train),(x_test,t_test)=load_mnist(normalize=True,flatten=True,one_hot_label=False)
returnx_test,t_test
 
definit_network():#会读入保存在pickle文件sample_weight.pkl中学习到的权重参数，这个文件中以字典变量的形式保存了权重和偏置参数
withopen("sample_weight.pkl",'rb')asf:
network=pickle.load(f)
returnnetwork
 
defpredict(network,x):#定义预测函数
W1,W2,W3=network['W1'],network['W2'],network['W3']
b1,b2,b3=network['b1'],network['b2'],network['b3']
a1=np.dot(x,W1)+b1
z1=sigmoid(a1)
a2=np.dot(z1,W2)+b2
z2=sigmoid(a2)
a3=np.dot(z2,W3)+b3
y=softmax(a3)
returny
 
x,t=get_data()
network=init_network()
accuracy_cnt=0
foriinrange(len(x)):#取出保存在x中的图像数据
y=predict(network,x[i])#以numpy数组的形式输出各个标签对应的概率
p=np.argmax(y)#获取学习率最高的元素索引
ifp==t[i]:#如果预测的数字和标签一致
accuracy_cnt+=1#预测对的数加一
 
print("Accuracy:"+str(float(accuracy_cnt)/len(x)))#预测准确率为预测正确的个数/所有图片（标签）的数量

在这个例子当中，我们把load_mnist函数的参数normalize设置成了True。将normalize设置成true以后，函数内部会进行转换，将图像各个像素值除以255，是的数据的值在0-1之间。像这样把数据限定在某个范围内的处理称为正规化（normalization）。此外对神经网络的输入数据进行某种既定的转换称为预处理（pre-pressing）

3.6.3 批处理

上面实现了mnist数据集的神经网络，下面关注一下神经网络的权重和偏置

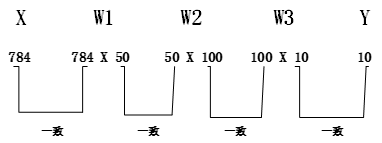
从整体流程图可以看出，输入一个由784像素（原本是28x28的二维数组）构成的一维数组后，输出一个有10个元素的一维数组，这是只输入一张图像数据处理的流程。
接下来考虑打包输入多张图，假设我们用predict()函数一次性打包100张图像，因此可以把x的形状改为100x784。

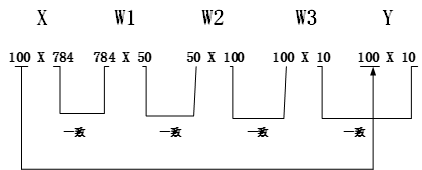
如图所示，输入数据的形状为100X784，输出数据的形状为100X10。这表示输入的100张图的结果被一次性输出了。比如x[0],y[0]保存了第0张图像及其推理结果。

这种打包式的输入数据称为批（batch）。批有捆的意思，图像就如同纸币一样被扎成一捆。

tips：批处理对计算机的运算有极大好处，可以大幅缩短每张图像的处理时间，因为大多数处理数值计算的库都进行了能够高效处理大型数据运算的最优化。也就是说批处理一次性计算大型数组要比分开逐步计算各个小型数组运算速度更快。

x,t=get_data()
network=init_network()
batch_size=100#设置批的数量
accuracy_cnt=0
 
for i in range(0,len(x),batch_size):
    x_batch=x[i:i+batch_size]
    y_batch=predict(network,x_batch)
    p=np.argmax(y_batch,axis=1)
    accuracy_cnt+=np.sum(p==t[i:i+batch_size])
    
print("Accuracy:"+str(float(accuracy_cnt/len(x))))

在range（）函数生成的列表基础上，通过x[i:i+batch_size]从输入数据组抽取批数据，x[i:i+batch_size]会取出从第i个到第i+batch_size个之间的数据。本例子是像x[0:100],x[100:200]……

然后通过softmax（）获取值最大元素的索引。需要注意的是，给定了参数axis=1。这里指定了在100x10的数组中，沿着第一维度（行）找到值最大元素的索引（第0维对应第1个维度）

3.7本章小结

1.神经网络中的激活函数使用平滑变换的sigmoid函数或者ReLU函数
2.通过巧妙的使用Numpy多维数组，可以高效地实现神经网络
3.机器学习的问题大体上可以分为回归问题和分类问题
4.关于输出层的激活函数，回归问题中一般用恒等函数，分类问题一般用softmax函数
5.分类问题中，输出层的神经元数量设置为要分类的类别数量
6.输入数据的合集称为批。通过以批为单位进行推理处理，能够实现高速运算