DFS
目录
一,树的DFS和BFS
二,DFS是栈,BFS是队列
三,系统栈也是DFS
四,图的DFS和BFS
五,常见搜索问题分类
1,显式树
2,隐式树
3,显式图
4,隐式图
六,DFS实战
1,显式树
二叉树
2,隐式树
CSU 1013 狐狸与小狗
HDU 1016 Prime Ring Problem(素数环,全排列问题)
HDU 1455 Sticks(组合)
SGU 454 Kakuro
力扣 756. 金字塔转换矩阵
力扣 254. 因子的组合
力扣 291. 单词规律 II
力扣 351. 安卓系统手势解锁
力扣 698. 划分为k个相等的子集
3,显式图
CSU 1660 K-Cycle
CCF-CSP-2015-12-4 送货
4,隐式图
HDU 2614 Beat
CCF-CSP-2013-12-5 I’m stuck!
力扣 130. 被围绕的区域
力扣 302. 包含全部黑色像素的最小矩形
力扣 490. 迷宫
力扣 79. 单词搜索
七,深度优先树、森林
1,无向图
2,有向图
八,总结
一,树的DFS和BFS
![]()
DFS的搜索结果是:1 2 3 4 5 6 7 8
BFS的搜索结果是:1 2 6 3 4 7 8 5
简单的说,DFS就是不停的往下搜索,不停的往上回溯的过程,BFS就是一层一层的遍历的过程。
二,DFS是栈,BFS是队列
DFS其实就是一个不停入栈出栈的过程,BFS是用队列完成一层一层的搜索。
对于绝大部分搜索问题,如果能用DFS,那就能用BFS,反之亦然。
有些不仅要搜索节点还要附带给出从根到此节点的路径的问题,虽然理论上BFS也能写,但是写起来比DFS要麻烦很多。
三,系统栈也是DFS
无论是STL里面的stack,还是自定义栈,还是操作系统堆栈的栈,都是DFS
例如如下代码:
#include
using namespace std;
int main() {
for(int i=0;i<3;i++){
cout<<" A"< 输出:
A0 B0 C0 C1 C2 B1 C0 C1 C2 B2 C0 C1 C2 A1 B0 C0 C1 C2 B1 C0 C1 C2 B2 C0 C1 C2 A2 B0 C0 C1 C2 B1 C0 C1 C2 B2 C0 C1 C2
也就是说,暴力枚举的for循环套for循环,其实就是用系统栈做DFS。同理,递归也是用系统栈做DFS
四,图的DFS和BFS
图按照某种映射关系,可以直接映射成树,所以图的DFS和BFS本质上和树是一样的。
通常,我们不会显式定义,图怎么样映射到树,其中的细节隐藏在代码细节中,所以每个人写出来的图的DFS和BFS都不尽相同,而不像树的搜索方式是唯一的。
当然,同一个问题,怎么样抽象成一棵树或者一个图,每个人的实现细节也是不尽相同的。
一般来讲,如果研究对象本身就是树或者图,那么解空间结构也就是对应的树或者图,不过也有例外,比如N皇后问题。
五,常见搜索问题分类
1,显式树
例如搜索某二叉树,查找值最大的节点
2,隐式树
例如暴力枚举、数独、N皇后问题、排列问题、组合问题
3,显式图
例如搜索某图
4,隐式图
例如搜索迷宫、棋盘
六,DFS实战
1,显式树
二叉树
多叉 树
2,隐式树
CSU 1013 狐狸与小狗
题目:
Description
Upwinder最近喜欢上了一款古老的起源于Scandinavia(斯堪迪纳维亚半岛)的小游戏。具体的游戏规则如下:
1. 棋盘设定
棋盘的大小为8行8列,有两个玩家:狐狸和小狗。初始的时候有4只小狗被放置在棋盘最上边一行的4个黑色格子里;而1只狐狸被放在最下边一行的某个黑色格子里。以棋盘左上角为原点,向下为行的正方向,向右为列的正方向,从1开始给每一个格子编号,如图1所示。
2. 移动规则
(1) 两个玩家轮流下棋。
(2) 狐狸每轮可以斜着向上或斜着向下移动至相邻的一个空格子,只能移动一步;
(3) 小狗每轮只能斜着向下移动至相邻的一个空格子,只能移动一只,且只能移动一步;
(4) 显然根据移动规则棋盘中只有黑色的格子才能放棋子
3. 游戏目标
狐狸与小狗的目标是不同的。
(1) 如果小狗将狐狸围住致使其无法移动(包括围在边界),那么小狗获胜(参考图2-A,B,C)。
(2) 如果狐狸到达了棋盘最上方一行的任意一个黑色格子,那么狐狸获胜(参考图2-D);
特别的,游戏不存在平局或死局,而且如果4只小狗均无法移动,则狐狸可以一直移动直至取胜。
现在告诉你游戏过程中的某一个局面,你能帮Upwinder判断如果狐狸与小狗均采取最优策略的话,谁能取得最后的胜利吗?
Input
第一行一个数字T表示接下来有T(T<=3000)种局面。
对于每一种局面,由三行数据组成,其中:
第一行为整数0或1。0代表当前狐狸掌握棋权,1代表当前小狗掌握棋权。
第二行为两个整数,以空格分隔,依次是狐狸在棋盘上的行坐标Fr和列坐标Fl。
第三行为八个整数,以空格分隔,依次是第一只小狗的行坐标Dr1,列坐标Dl1……以此类推。
Output
对于每一种局面,仅输出一行。
如果狐狸能够取胜,请输出“Fox win”(不含引号)
如果小狗能够取胜,请输出“Dog win”(不含引号)
Sample Input
4
0
4 4
3 3 3 5 5 3 5 5
1
1 3
3 1 2 4 3 5 4 4
0
5 3
3 3 3 5 3 7 2 8
1
7 7
6 4 5 5 4 6 4 8
Sample Output
Dog win
Fox win
Fox win
Dog win
思路:
首先对32个格子编号,0-31
4个狗的编号为b1,b2,b3,b4,狐狸的编号为c
每次都保持b1 其次是胜负判断,如果c 代码: 题目: 描述 圆环由n个圆组成,如图所示。将自然数1、2,...,n分别放入每个圆,两个相邻圆中的数字总和应为质数。 输入值 n(0 输出量 输出格式如下所示。每一行代表环中从顺时针和逆时针1开始的一系列圆圈编号。数字顺序必须满足以上要求。按字典顺序打印解决方案。 样本输入 6 8 样本输出 情况1: 情况2: 首先注意到,只有n是偶数的时候才有解,所以实际上n只是2到18这9个偶数而已。 如果追求效率的话,可以硬编码9个字符串,换行的问题还要注意一下。 因为后来提交之后没有出现超时,所以就没有这么做。 既然n最多18,那么2个数的和最多也就35,不超过35的素数只有10个,所以本题的素数判断也是硬编码的。 注意:如果在递归的函数(例如这里的place函数)里面使用嵌套的循环,一定要搞清楚continue和break的作用对象是哪个循环。 代码: 题目: Description George took sticks of the same length and cut them randomly until all parts became at most 50 units long. Now he wants to return sticks to the original state, but he forgot how many sticks he had originally and how long they were originally. Please help him and design a program which computes the smallest possible original length of those sticks. All lengths expressed in units are integers greater than zero. Input The input contains blocks of 2 lines. The first line contains the number of sticks parts after cutting, there are at most 64 sticks. The second line contains the lengths of those parts separated by the space. The last line of the file contains zero. Output The output file contains the smallest possible length of original sticks, one per line. Sample Input 9 Sample Output 6 题意:把数组分成一些组,使得每个组的和都是r,求r的最小值。 这个题目主要是自己思路不清晰。 最开始提交的时候写的递归函数居然只有2个参数,后来参数越来越多。。。 直到最后有6个参数才对。 昨天(7.22)最后的代码是这样的: 到晚上看到别人15ms甚至0ms就运行结束,自己的代码却超时,感觉很震惊。 感觉会有2种情况,要不是某个测试用例让我的代码陷入了死循环,要不就是哪个地方写的不对,造成了非常恐怖的重复无效运算。 到了晚上1点半,终于想通了,果然是有太多重复了。 place函数的主体是 这样,每次这个i都是可以任选1个数的,相当于把组合的问题变成了排列了,于是就造成了阶乘级别的重复计算,难怪超时。 正确代码: 题目: Kakuro puzzle is played on a nx m grid of "black" and "white" cells. Apart from the top row and leftmost column which are entirely black, the grid has some amount of white cells which form "runs" and some amount of black cells. "Run" is a vertical or horizontal maximal one-lined block of adjacent white cells. Each row and column of the puzzle can contain more than one "run". Every white cell belongs to exactly two runs — one horizontal and one vertical run. Each horizontal "run" always has a number in the black half-cell to its immediate left, and each vertical "run" always has a number in the black half-cell immediately above it. These numbers are located in "black" cells and are called "clues". Given the grid, your task is to find a solution for the puzzle. Input The first line of input contains two integers n and m (2 ≤ n , m ≤ 6) — the number of rows and columns correspondingly. Each of the next n lines contains descriptions of m cells. Each cell description is one of the following 5-character strings: ..... — "white" cell; The first row and the first column of the grid will never have any white cells. The given grid will have at least one "white" cell. Output Print n lines to the output with m cells in each line. For every "black" cell print ' ' (underscore), for every "white" cell print the corresponding digit from the solution. Delimit cells with a single space, so that each row consists of 2m-1 characters. Example(s) sample input 6 6 sample output _ _ _ _ _ _ sample input 3 3 sample output _ _ _ 题意: 根据输入的信息,求解数字表格。 输入的信息包括,表格中哪些格子无效,哪些格子有数,对于同一行或同一列的连续格子,和是多少。 代码: 然而还是在第218个测试用例超时了 你正在把积木堆成金字塔。每个块都有一个颜色,用一个字母表示。每一行的块比它下面的行 少一个块 ,并且居中。 为了使金字塔美观,只有特定的 三角形图案 是允许的。一个三角形的图案由 两个块 和叠在上面的 单个块 组成。模式是以三个字母字符串的列表形式 allowed 给出的,其中模式的前两个字符分别表示左右底部块,第三个字符表示顶部块。 例如,"ABC" 表示一个三角形图案,其中一个 “C” 块堆叠在一个 'A' 块(左)和一个 'B' 块(右)之上。请注意,这与 "BAC" 不同,"B" 在左下角,"A" 在右下角。 在给定 bottom 和 allowed 的情况下,如果你能一直构建到金字塔顶部,使金字塔中的 每个三角形图案 都是允许的,则返回 true ,否则返回 false 。 示例 1: 输入:bottom = "BCD", allowed = ["BCC","CDE","CEA","FFF"] 输入:bottom = "AAAA", allowed =["AAB","AAC","BCD","BBE","DEF"] 提示: 2 <= bottom.length <= 6 https://blog.csdn.net/nameofcsdn/article/details/113131253 https://blog.csdn.net/nameofcsdn/article/details/113131253 https://blog.csdn.net/nameofcsdn/article/details/113131253 https://blog.csdn.net/nameofcsdn/article/details/113132857 题目: Description A simple cycle is a closed simple path, with no other repeated vertices or edges other than the starting and ending vertices. The length of a cycle is the number of vertices on it. Given an undirected graph G(V, E), you are to detect whether it contains a simple cycle of length K. To make the problem easier, we only consider cases with small K here. Input There are multiple test cases. Output For each test case, you should output “YES” in one line if there is a cycle of length K in the given graph, otherwise output “NO”. Sample Input Sample Output 有毒啊。。 神坑啊。。。 为我逝去的3小时青春不值。。。 我的代码是这样的: 感觉几乎没法优化了,怎么会超时呢? 而且他们都是一批一批的0msAC 于是我访问同学的博客,拿他的源代码做了个小测试,可以AC,但是找不到下图里面k为5的环 (我并不是想讽刺他,其实他很牛的。我只是想吐槽OJ坑我。 只不过在一个算法无论如何优化都超时的情况下,我们都会选择想办法找一个更好的算法。 然而这个题目,有可能正确代码都是要超时的,也有可能只是OJ给的测试用例比较少,没有下图中的情况。 鉴于下图有很高的一般性,我选择相信前者。 我只是基本上考虑清楚了才会写,所以才偶然发现他们用的算法不对) 输入 2 5 6 5 一笔画 题目: Description Zty is a man that always full of enthusiasm. He wants to solve every kind of difficulty ACM problem in the world. And he has a habit that he does not like to solve Input The input contains multiple test cases. Output For each test case output the maximum number of problem zty can solved. Sample Input 3 Sample Output 3 2 4 Hint 巨坑! 且不说Hint写的是错的,因为这并没有影响我理解题意。 但是! 对角线根本就没有意义,然后看那三组输入示例,我下意识的以为输入的对角线应该都是0吧。 10点39第一次提交就是Wrong Answer,后面一直是错的,然后中午睡了会,下午继续分析, 代码被化简到了非常恐怖的地步,然而还是Wrong Answer。 然后和同学讨论题意,看是不是我理解错了。但是没有!题意就是我理解的那样! 讨论的过程中无意间想到,输入的对角线不一定都是0,这个地方会导致我的计算错误。 我的代码是: 之前就是因为main函数里面少了一句list[0][0]=0; 所以就错了。 超级坑爹啊啊啊啊。。。。 当然,这个代码还有点问题,时间代价是正常代码的指数级倍。运行时间是1326 ms 稍作修改即可得到运行时间为62 ms的代码: CCF-CSP 2013-2015 题目: 给定一个二维的矩阵,包含 'X' 和 'O'(字母 O)。 找到所有被 'X' 围绕的区域,并将这些区域里所有的 'O' 用 'X' 填充。 示例: X X X X X X X X 被围绕的区间不会存在于边界上,换句话说,任何边界上的 'O' 都不会被填充为 'X'。 任何不在边界上,或不与边界上的 'O' 相连的 'O' 最终都会被填充为 'X'。如果两个元素在水平或垂直方向相邻,则称它们是“相连”的。 代码: 图片在计算机处理中往往是使用二维矩阵来表示的。 给你一个大小为 m x n 的二进制矩阵 image 表示一张黑白图片,0 代表白色像素,1 代表黑色像素。 黑色像素相互连接,也就是说,图片中只会有一片连在一块儿的黑色像素。像素点是水平或竖直方向连接的。 给你两个整数 x 和 y 表示某一个黑色像素的位置,请你找出包含全部黑色像素的最小矩形(与坐标轴对齐),并返回该矩形的面积。 你必须设计并实现一个时间复杂度低于 O(mn) 的算法来解决此问题。 示例 1: 输入:image = [["1"]], x = 0, y = 0 提示: m == image.length 思路: 关于连通性的题目我一般用并查集,不过这题附加条件是时间复杂度小于O(mn),那我就用DFS吧。 puzzle(017.1)Orac 给定一个二维网格和一个单词,找出该单词是否存在于网格中。 单词必须按照字母顺序,通过相邻的单元格内的字母构成,其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。 示例: board = 给定 word = "ABCCED", 返回 true 提示: board 和 word 中只包含大写和小写英文字母。 连通图的深度优先搜索,在遍历的过程中会产生深度优先树。 不连通的图如果全部搜索完,则产生由多个深度优先树组成的森林。 对于无向图,有多少个连通分量,就需要多少次独立的DFS。 如果一个无向连通图中有一个长为n的环,那么对应的深度优先树至少有n层 比如这个图,深度优先树一定是6层,具体是什么样的树取决于起点和搜索方向偏好排序。 而这这个图,深度优先树可能会是4层。 对于有向图,每个退化连通分量的搜索都是独立的。 对于每个退化连通分量,DFS的结果都可能是一个深度优先森林 1,DFS和BFS并没有很强的界限,往往能用DFS的往往也可以用BFS,反之亦然,只不过编码复杂程度可能不同。 如果子问题性质很明显,则适合用DFS。 如果解空间的层次这个抽象概念,能对应到具体概念,则适合用BFS。 如果解空间的路径这个抽象概念,能对应到具体概念,则适合用DFS(即回溯算法)。 2,DFS和DP并没有很强的界限,比如树的DFS和树形DP往往就界限很模糊。其实其他算法往往也会建立在DFS的基础之上。 3,DFS和暴力搜索并没有很强的界限,循环套循环就是DFS式的搜索。正因为如此,很多算法也会建立在DFS的基础之上。 DFS其他实战: 同一个世界 计算机求解 水排序谜题 or 水排序谜题 颜色方块 树形DP dancing links#includeHDU 1016 Prime Ring Problem(素数环,全排列问题)
注意:第一个圆的数目应始终为1。
您将编写一个完成上述过程的程序。
在每种情况下都打印空白行。
1 4 3 2 5 6
1 6 5 2 3 4
1 2 3 8 5 6 7 4
1 2 5 8 3 4 7 6
1 4 7 6 5 8 3 2
1 6 7 4 3 8 5 2#includeHDU 1455 Sticks(组合)
5 2 1 5 2 1 5 2 1
4
1 2 3 4
0
5 #includefor (int i = 0; i < n; i++)
{
if (b[i] && list[i] <= su)
{
su -= list[i];
b[i] = false;
if (place(list, b, summ, su, n))return true;
b[i] = true;
su += list[i];
}
}#includeSGU 454 Kakuro
The rules of the puzzle are simple:
XXXXX — "black" cell with no clues;
AA\BB— "black" cell with one or two clues. AA is either a 2-digit clue for the corresponding vertical run, or XX if there is no associated vertical run. BB is either a 2-digit clue for the corresponding horizontal run, or XX if there is no associated horizontal run.
It is guaranteed that the given puzzle has at least one solution.
If there are many solutions, you may output any of them.
XXXXX XXXXX 28\XX 17\XX 28\XX XXXXX
XXXXX 22\22 ..... ..... ..... 10\XX
XX\34 ..... ..... ..... ..... .....
XX\14 ..... ..... 16\13 ..... .....
XX\22 ..... ..... ..... ..... XXXXX
XXXXX XX\16 ..... ..... XXXXX XXXXX
_ _ 5 8 9 _
_ 7 6 9 8 4
_ 6 8 _ 7 6
_ 9 2 7 4 _
_ _ 7 9 _ _
XXXXX 04\XX XXXXX
XX\04 ..... XXXXX
XXXXX XXXXX XXXXX
_ 4 _
_ _ _#include力扣 756. 金字塔转换矩阵
你从底部的一排积木 bottom 开始,作为一个单一的字符串,你 必须 使用作为金字塔的底部。
输出:true
解释:允许的三角形模式显示在右边。
从最底层(第3层)开始,我们可以在第2层构建“CE”,然后在第1层构建“E”。
金字塔中有三种三角形图案,分别是“BCC”、“CDE”和“CEA”。都是允许的。
示例 2:
输出:false
解释:允许的三角形模式显示在右边。
从最底层(游戏邦注:即第4个关卡)开始,创造第3个关卡有多种方法,但如果尝试所有可能性,你便会在创造第1个关卡前陷入困境。
0 <= allowed.length <= 216
allowed[i].length == 3
所有输入字符串中的字母来自集合 {'A', 'B', 'C', 'D', 'E', 'F', 'G'}。
allowed 中所有值都是 唯一的class Solution {
public:
bool dfs(string& bottom, string& b2, map力扣 254. 因子的组合
力扣 291. 单词规律 II
力扣 351. 安卓系统手势解锁
力扣 698. 划分为k个相等的子集
3,显式图
CSU 1660 K-Cycle
The first line will contain a positive integer T (T ≤ 10) meaning the number of test cases.
For each test case, the first line contains three positive integers N, M and K ( N ≤ 50, M ≤ 500, 3 ≤ K ≤ 7). N is the number of vertices of the graph, M is the number of edges and K is the length of the cycle desired. Next follow M lines, each line contains two integers A and B, describing an undirected edge AB of the graph. Vertices are numbered from 0 to N-1.2
6 8 4
0 1
1 2
2 0
3 4
4 5
5 3
1 3
2 4
4 4 3
0 1
1 2
2 3
3 0
YES
NO#include
0 1
1 2
2 3
3 0
0 4
4 1
就输出NOCCF-CSP-2015-12-4 送货
4,隐式图
HDU 2614 Beat
a problem that is easy than problem he had solved. Now yifenfei give him n difficulty problems, and tell him their relative time to solve it after solving the other one.
You should help zty to find a order of solving problems to solve more difficulty problem.
You may sure zty first solve the problem 0 by costing 0 minute. Zty always choose cost more or equal time’s problem to solve.
Each test case include, first one integer n ( 2< n < 15).express the number of problem.
Than n lines, each line include n integer Tij ( 0<=Tij<10), the i’s row and j’s col integer Tij express after solving the problem i, will cost Tij minute to solve the problem j.
0 0 0
1 0 1
1 0 0
3
0 2 2
1 0 1
1 1 0
5
0 1 2 3 1
0 0 2 3 1
0 0 0 3 1
0 0 0 0 2
0 0 0 0 0 Hint: sample one, as we know zty always solve problem 0 by costing 0 minute. So after solving problem 0, he can choose problem 1 and problem 2, because T01 >=0 and T02>=0. But if zty chooses to solve problem 1, he can not solve problem 2, because T12 < T01. So zty can choose solve the problem 2 second, than solve the problem 1. #include#includeCCF-CSP-2013-12-5 I’m stuck!
力扣 130. 被围绕的区域
X O O X
X X O X
X O X X
运行你的函数后,矩阵变为:
X X X X
X X X X
X O X X
解释:class Solution {
public:
void solve(vector力扣 302. 包含全部黑色像素的最小矩形
输入:image = [["0","0","1","0"],["0","1","1","0"],["0","1","0","0"]], x = 0, y = 2
输出:6
示例 2:
输出:1
n == image[i].length
1 <= m, n <= 100
image[i][j] 为 '0' 或 '1'
1 <= x < m
1 <= y < n
image[x][y] == '1'
image 中的黑色像素仅形成一个 组件class Solution {
public:
int id(int x, int y)
{
return x * col + y;
}
vector力扣 490. 迷宫
力扣 79. 单词搜索
[
['A','B','C','E'],
['S','F','C','S'],
['A','D','E','E']
]
给定 word = "SEE", 返回 true
给定 word = "ABCB", 返回 false
1 <= board.length <= 200
1 <= board[i].length <= 200
1 <= word.length <= 10^3
int flatRow[4] = { 0, -1, 0, 1 };
int flatCol[4] = { 1, 0, -1, 0 };
bool existFromPointS(char** board, int boardSize, int* boardColSize, char * word,int rowS,int colS){
if (word[0] == '\0'){
return true;
}
if (rowS < 0 || rowS >= boardSize || colS < 0 || colS >= *boardColSize){
return false;
}
if (board[rowS][colS] != word[0]){
return false;
}
board[rowS][colS] = '\0';
int i;
for (i = 0; i < 4; i++){
if (existFromPointS(board, boardSize, boardColSize, word + 1, rowS + flatRow[i], colS + flatCol[i])){
return true;
}
}
board[rowS][colS] = word[0];
return false;
}
bool exist(char** board, int boardSize, int* boardColSize, char * word){
int row, col;
for (row = 0; row < boardSize; row++){
for (col = 0; col < *boardColSize; col++){
if (existFromPointS(board, boardSize, boardColSize, word, row, col)){
return true;
}
}
}
return false;
}七,深度优先树、森林
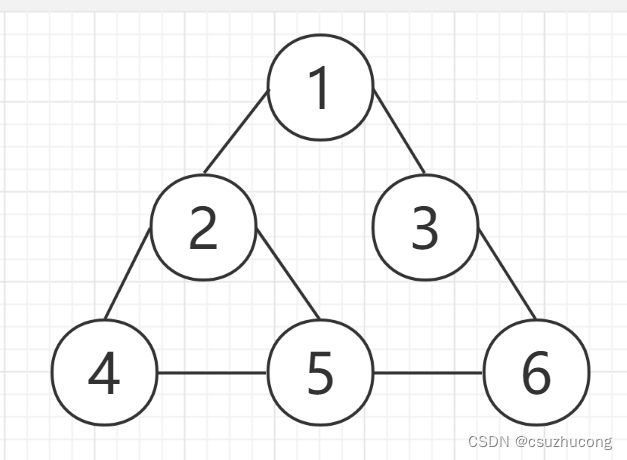
1,无向图
2,有向图
八,总结