代码随想录刷题笔记(DAY4)
今日总结:今天把中心放在前端学习上,最后一个题没有完全理解,明天早起补上吧。勉强算完成任务。(已补上)
Day 4
01. 两两交换链表中的节点(No. 24)
题目链接
代码随想录题解
1.1 题目
给你一个链表,两两交换其中相邻的节点,并返回交换后链表的头节点。你必须在不修改节点内部的值的情况下完成本题(即,只能进行节点交换)。
示例 1:
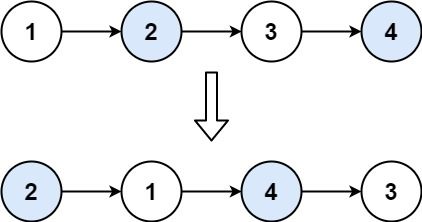
输入:head = [1,2,3,4]
输出:[2,1,4,3]
示例 2:
输入:head = []
输出:[]
示例 3:
输入:head = [1]
输出:[1]
1.2 笔记
先来分析需不需要虚拟头节点,虚拟头节点是为了让处理头节点的方式和处理其他节点的方式相同,不用再单独写出来,所以先考虑头节点和其他节点的处理方式是否一样:
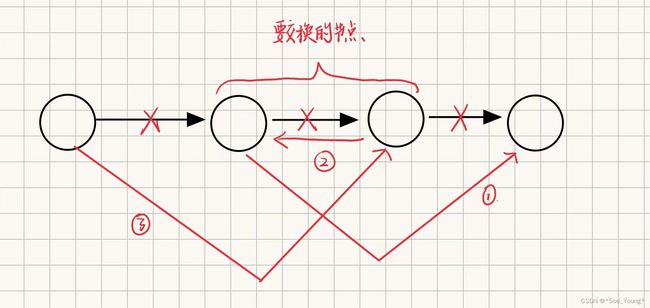
交换一个中间的节点需要哪些操作呢?
需要将前一个节点,也就是上图第一个点指向第三个点,但是头节点并没有前一个节点,所以我们得出头节点和其他节点的处理方式是不同的,所以引入虚拟头节点。(上图是要进行的操作,标号不代表顺序)
也很容易能看出,要交换两个节点需要前一个节点和后一个节点,所以我们的 cur 要定义在前一个节点:
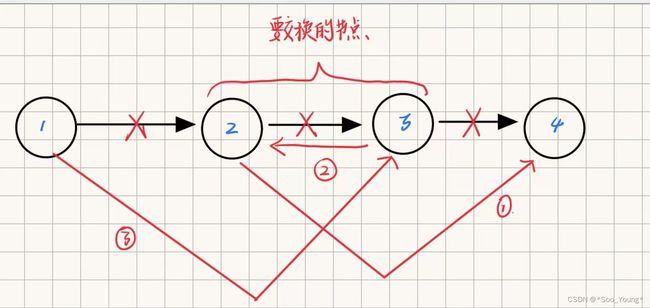
这里我们先给上个图加上序号
- 先让
cur指向它的下下个节点(3 节点),但这时我们发现cur的下一个节点(2 节点)是不可达的,定义temp1指向这个节点
- 使得
temp1(节点 2 )的下一个节点指向 (节点 4)
- 让 (节点 3)再指向 (节点2)这样拉直后就实现了反转
接下来我们来看循环遍历的出口,如果是偶数个元素的话我们要保证 cur 后面有一个元素(有一个元素就代表后面还有一组元素,还需要循环交换),奇数个元素的话则需要保证 cur 的后面有两个个元素就结束(有两个元素才需要交换,一个的话不需要交换直接结束),先尝试写出循环遍历的出口
while(cur.next.next != null)
while(cur.next != null)
很明显看出这两个是包含关系,则可以写出
while(cur.next != null && cur.next.next != null)
1.3 代码
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode() {}
* ListNode(int val) { this.val = val; }
* ListNode(int val, ListNode next) { this.val = val; this.next = next; }
* }
*/
class Solution {
public ListNode swapPairs(ListNode head) {
ListNode dummyHead = new ListNode(0, head); // 虚拟头节点
ListNode cur = dummyHead;
ListNode temp1; // 临时节点
ListNode temp2;
while (cur.next != null && cur.next.next != null) {
temp1 = cur.next;
cur.next = cur.next.next;
temp1.next = cur.next.next;
cur.next.next = temp1;
cur = cur.next.next;
}
return dummyHead.next;
}
}
02. 删除链表的倒数第 N 个结点(No. 19)
题目链接
代码随想录题解
1.1 题目
给你一个链表,两两交换其中相邻的节点,并返回交换后链表的头节点。你必须在不修改节点内部的值的情况下完成本题(即,只能进行节点交换)。
示例 1:
输入:head = [1,2,3,4]
输出:[2,1,4,3]
示例 2:
输入:head = []
输出:[]
示例 3:
输入:head = [1]
输出:[1]
1.2 笔记
这道题的关键是如何找到删除节点的前一个节点,然后我们只需要让 node.next = node.next.next 就完成了删除操作,下面来思考如何找到这个节点呢?
因为题目里面给的是倒数第 N 个节点,所以很容易想到倒序遍历链表,回顾一下如何倒序遍历链表呢?
public void backtracking(ListNode head) {
if (head.next == null) {
// 到了最后一个节点
return head;
}
ListNode node = head; // 记录当前栈中的 head
backtracking(head.next);
System.sout.println(node); // 实现倒叙输出
}
这道题的思路就变得清晰起来了,递归遍历到最后一个节点然后我们开始计数,直到倒数第 N 个节点的前一个节点,就比如 1 的话需要在倒数第二个栈执行操作,可以写出
if (--N == 0) {
// 要删除的节点的前一个节点
node.next = node.next.next;
return;
}
下面给出完整的代码
1.3 代码
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode() {}
* ListNode(int val) { this.val = val; }
* ListNode(int val, ListNode next) { this.val = val; this.next = next; }
* }
*/
class Solution {
int N = 0;
ListNode dummyNode = new ListNode();
public ListNode removeNthFromEnd(ListNode head, int n) {
N = n;
dummyNode.next = head;
backtracking(dummyNode);
return dummyNode.next;
}
public void backtracking(ListNode head) {
if (head.next == null) {
// 最后一个节点
return;
}
backtracking(head.next);// 递归遍历节点
ListNode node = head;
if (--N == 0) {
// 要删除的节点的前一个节点
node.next = node.next.next;
return;
}
return;
}
}
03. 环形链表 II(No. 142)
题目链接
代码随想录题解
3.1 题目
给定一个链表的头节点 head ,返回链表开始入环的第一个节点。 如果链表无环,则返回 null。
如果链表中有某个节点,可以通过连续跟踪 next 指针再次到达,则链表中存在环。 为了表示给定链表中的环,评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置(索引从 0 开始)。如果 pos 是 -1,则在该链表中没有环。注意:pos 不作为参数进行传递,仅仅是为了标识链表的实际情况。
不允许修改 链表。
示例 1:
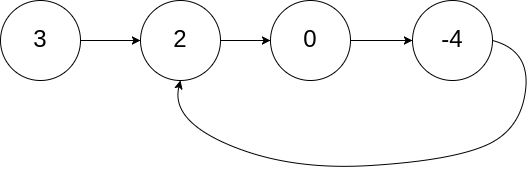
输入:head = [3,2,0,-4], pos = 1
输出:返回索引为 1 的链表节点
解释:链表中有一个环,其尾部连接到第二个节点。
示例 2:
输入:head = [1,2], pos = 0
输出:返回索引为 0 的链表节点
解释:链表中有一个环,其尾部连接到第一个节点。
示例 3:
输入:head = [1], pos = -1
输出:返回 null
解释:链表中没有环。
3.2 笔记
这道题的解法重点是数学推导过程,首先我们先解决如何确定有没有环:
设定一个快指针和一个慢指针,使得他们以两个节点和一个节点的速度向前移动,最后一定会相遇。
可以想象跑步时候被人套圈的场景,如果在一个圈中一个速度比另一个人快,最后一定会相遇,这是在现实的世界中,我们观察这两个人相遇的那个点不一定是整数点,因为最小单位不是一个整数。
但是在链表的圈内可以看作一个个往前跳动的,最小单位是一个个点,如果这两个指针相差的速度不是链表中两个点相差的最小单位的话,就有可能出现遇不到的情况,导致误判。
然后我们来确定相遇的位置:
我们从圈的入口到相遇处为 y,从相遇处到入口为 z 从起点到入口为 x,快节点首先进入环内,慢节点进入环的第一圈就被快节点追上(后面详细解释),写出公式经过推导可以得到最后一个公式,这个公式代表着什么意思呢?
就是从一个节点从起点出发,一个节点从 z 出发,他们最终会在 入口处 相遇。
为什么慢节点第一圈就会被追上呢?
因为慢节点走一圈,快节点就走了两圈,很明显可以发现快节点已经走过了慢节点走的路程,所以相遇一定是慢节点的第一圈。
3.3 代码
/**
* Definition for singly-linked list.
* class ListNode {
* int val;
* ListNode next;
* ListNode(int x) {
* val = x;
* next = null;
* }
* }
*/
public class Solution {
public ListNode detectCycle(ListNode head) {
ListNode fast = head;
ListNode slow = head;
// 如果没有环一定是快指针先到终点
while (fast != null && fast.next != null) {
fast = fast.next.next;
slow = slow.next;
if (fast == slow) {
// 说明快慢指针相遇了
ListNode index1 = fast;
ListNode index2 = head;
while (index1 != index2) {
index1 = index1.next;
index2 = index2.next;
}
return index1;
}
}
return null;
}
}