【CF闯关练习】—— 900分段
博客主页:PH_modest的博客主页
当前专栏:cf闯关练习
其他专栏:
每日一题
C++跬步积累
C语言跬步积累
座右铭:广积粮,缓称王!
一.关卡1(00:11(+1))
题目大意:
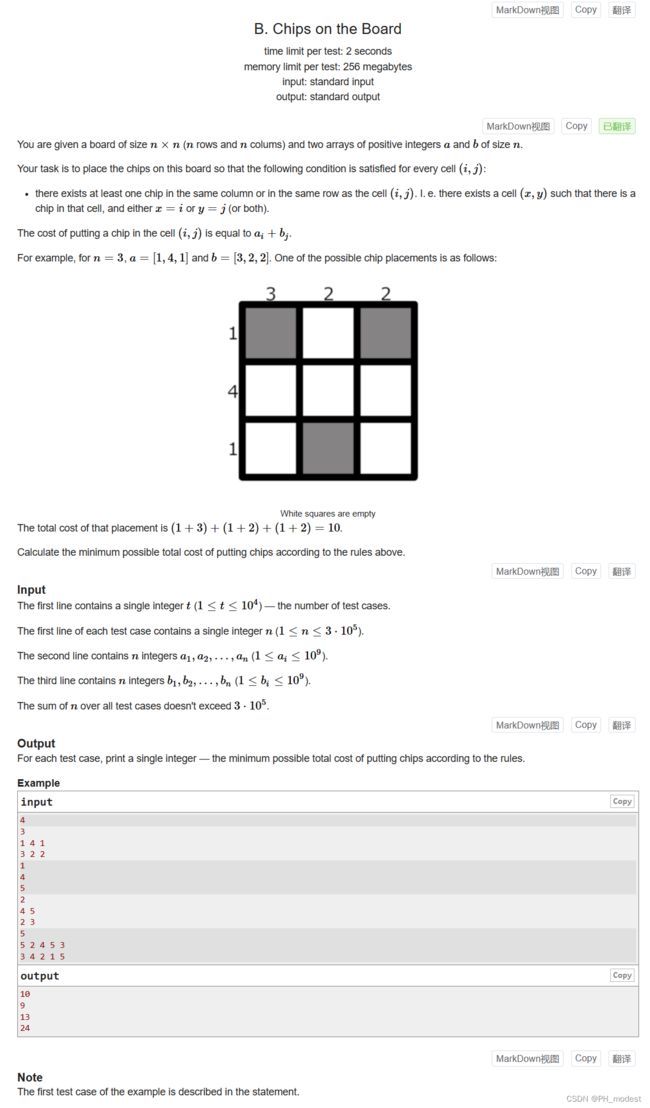
给你一个大小为 n ∗ n n * n n∗n的棋盘( n n n 行, n n n 列)和两个大小为 n n n 的正整数数组 a a a 和 b b b 。
你的任务是在棋盘上放置筹码,使每个单元格 ( i , j ) (i, j) (i,j) 都满足以下条件:
- 与 ( i , j ) (i, j) (i,j) 单元格在同一列或同一行中至少存在一个筹码。也就是说,存在这样一个单元格 ( x , y ) (x, y) (x,y) ,即该单元格中有一个筹码,并且 x = i x = i x=i 或 y = j y = j y=j (或两者都有)。
在 ( i , j ) (i, j) (i,j) 格中放入一个筹码的代价等于 a i + b j a_i + b _j ai+bj 。
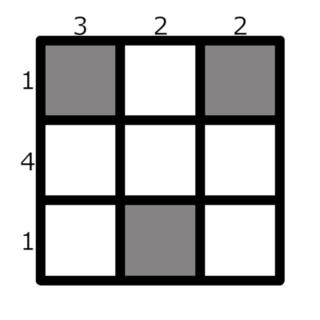
例如, n = 3 n=3 n=3 、 a = [ 1 , 4 , 1 ] a=[1, 4, 1] a=[1,4,1]和 b = [ 3 , 2 , 2 ] b=[3, 2, 2] b=[3,2,2] 。其中一种可能的筹码放置方式如下:
该布局的总成本为 ( 1 + 3 ) + ( 1 + 2 ) + ( 1 + 2 ) = 10 (1+3) + (1+2) + (1+2) = 10 (1+3)+(1+2)+(1+2)=10 。
请根据上述规则计算可能的最小筹码放置总成本。
1.Tutorial
分两种情况,①从数组a中找一个最小的数,分别和b数组相加;②从数组b中找一个最小的数,分别和a数组相加。最后取较小者
2.Solution
//https://codeforces.com/problemset/problem/1879/B
//00:11(-1)
//分两种情况,①从数组a中找一个最小的数,分别和b数组相加;②从数组b中找一个最小的数,分别和a数组相加。最后取较小者
//注意数据范围
#include3.Conclusion
注意数据范围,第一次写没注意范围以为是2e5结果TLE了,引以为戒
二.关卡2(00:09(+1))
题目大意:
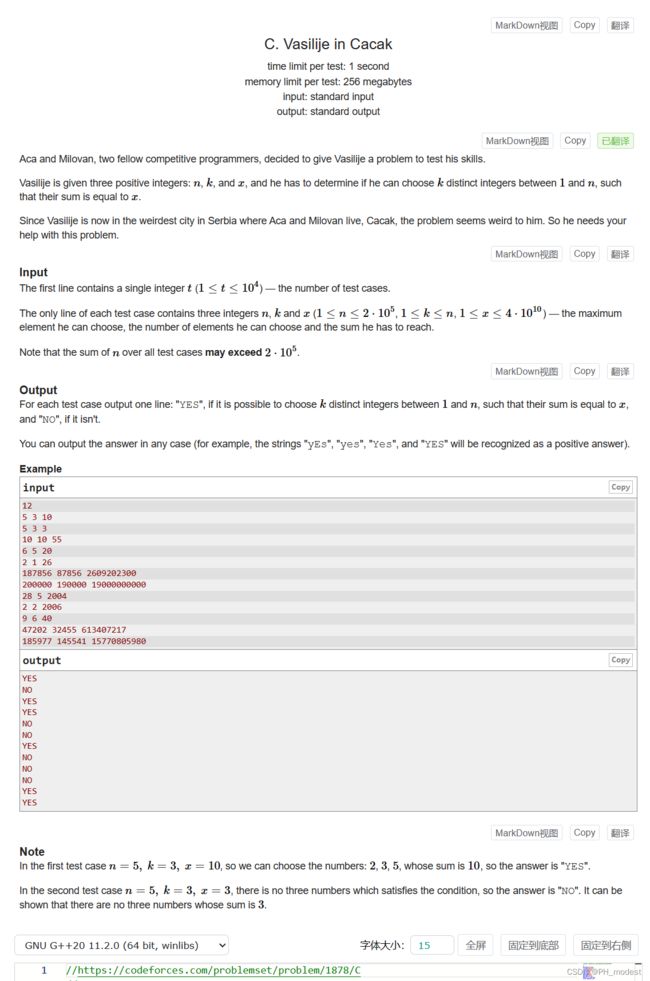
Aca 和 Milovan 是两位同为竞技程序员的朋友,他们决定给 Vasilije 出一道难题来测试他的技能。
给 Vasilije 三个正整数: n n n 、 k k k 和 x x x ,他必须判断能否在 1 1 1 和 n n n 之间选择 k k k 个不同的整数,使它们的和等于 x x x 。
由于瓦西里耶现在在塞尔维亚最奇怪的城市卡察克,也就是阿卡和米洛万居住的地方,所以他觉得这个问题很奇怪。所以他需要你的帮助来解决这个问题。
1.Tutorial
求出k个数字相加的最小值和最大值,注意求取时不要循环,直接用公式
2.Solution
//https://codeforces.com/problemset/problem/1878/C
//00:09(-1)
//求出k个数字相加的最小值和最大值,注意求取时不要循环,直接用公式
#include三.关卡3(00:20)
题目大意:
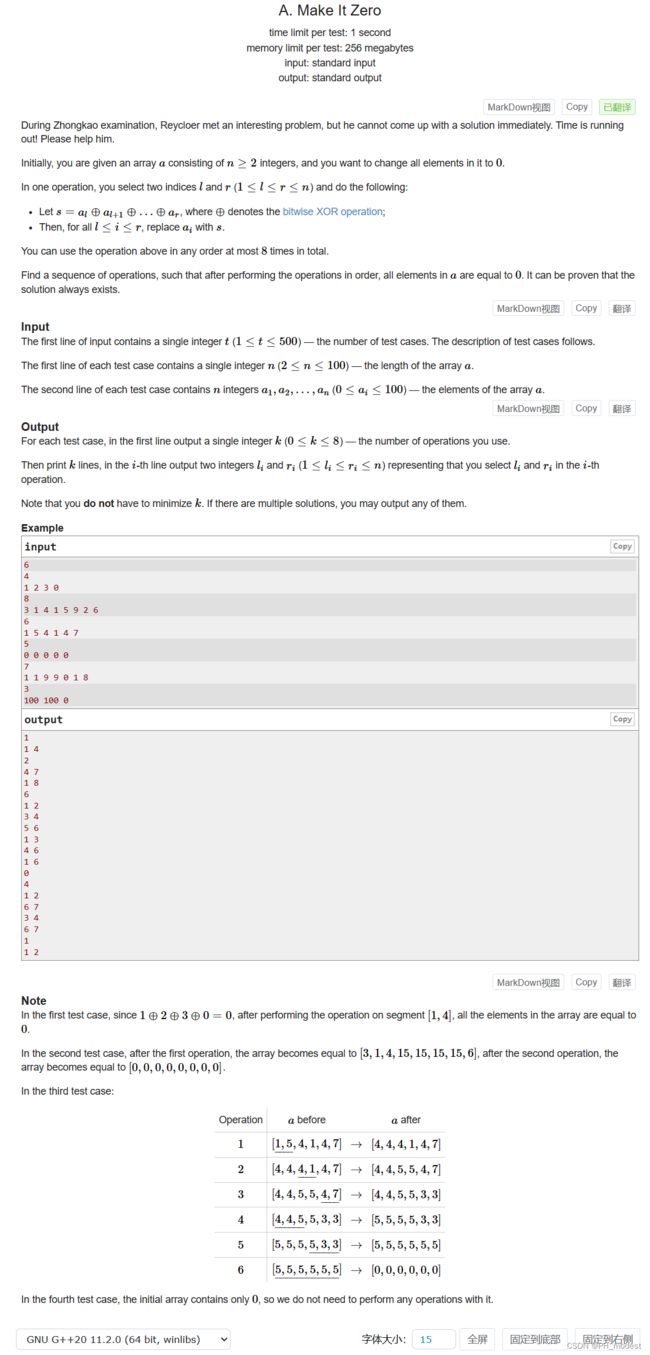
在中考期间,Reycloer 遇到了一个有趣的问题,但他无法立即想出解决办法。时间不多了!请帮助他。
最初,你得到一个由 n ≥ 2 n \ge 2 n≥2 个整数组成的数组 a a a ,你想将其中的所有元素都改为 0 0 0 。
在一次操作中,你选择两个索引 l l l 和 r r r ( 1 ≤ l ≤ r ≤ n 1\le l\le r\le n 1≤l≤r≤n ),并执行以下操作:
- 让 KaTeX parse error: Expected 'EOF', got '&' at position 5: s=a &̲#95; l\oplus a … ,其中 ⊕ \oplus ⊕ 表示 bitwise XOR 运算;
- 然后,对于所有 l ≤ i ≤ r l\le i\le r l≤i≤r ,用 s s s 替换 a i a _ i ai 。
上述操作以任何顺序进行,总共最多可以使用 8次。
找出一个运算序列,使得按顺序进行运算后,a中的所有元素都等于0。可以证明解总是存在的。
1.Tutorial
分两种情况:①n为偶数时,先将所有数从头到尾异或一遍,之后所有数都变成相同的数,再异或一遍所有数就变成0了,只需要2次;②n为奇数,方法和偶数一样,只不过多了几步,需要先将第一个数变为0,然后再将后面偶数个按照偶数的方法变为0,一共4次
2.Solution
//https://codeforces.com/problemset/problem/1869/A
//00:20
//分两种情况:①n为偶数时,先将所有数从头到尾异或一遍,之后所有数都变成相同的数,再异或一遍所有数就变成0了,只需要2次;②n为奇数,方法和偶数一样,只不过多了几步,需要先将第一个数变为0,然后再将后面偶数个按照偶数的方法变为0,一共4次
//
#include四.关卡4(WA)
传送门
题目大意:
括号序列是由字符"(“和/或”)"组成的字符串。正则括号序列是指可以通过在括号序列的原始字符之间插入字符 "1 "和 "+"来转换成正确算术表达式的括号序列。例如
- 括号序列"()() “和”(()) “是正则表达式(可分别转换为”(1)+(1) “和”((1+1)+1)");
- 括号序列")(“、”(“和”) "则不规则。
给你一个括号序列 s s s ,我们把它的长度定义为 n n n 。你的任务是找出一个长度为 2 n 2n 2n 的正则括号序列 t t t ,使得 s s s 不出现在括号序列 s s s 中。作为连续的子串不出现在 t t t 中,或者报告没有这样的序列。
1.Tutorial
- 如果有连续相同的就以()()的形式输出,如果没有就以(())的形式输出;
- 字符串判断是否有字串:ans.find(s)==string::npos,如果为真说明s不是ans的字串
2.Solution
//https://codeforces.com/problemset/problem/1860/A
//WA
//如果有连续相同的就以()()的形式输出,如果没有就以(())的形式输出
//字符串判断是否有字串:ans.find(s)==string::npos,如果为真说明s不是ans的字串
#include3.Conclusion
多考虑考虑特殊情况
五.关卡5(00:39(+1))
传送门
题目大意:
鲍勃和卡罗尔和爱丽丝玩了一整天,现在该回家了。爱丽丝、鲍勃和卡罗尔分别住在一个无限大的二维网格中的 A A A 、 B B B 和 C C C 单元格里。现在,他们都在 A A A 单元格中。
如果鲍勃(或卡罗尔)在某个单元格中,他(她)可以移动到邻近的单元格中。如果两个单元格共用一条边,则称为相邻单元格。例如, ( 3 , 5 ) (3, 5) (3,5) 单元格有四个相邻单元格: ( 2 , 5 ) (2, 5) (2,5) 、 ( 4 , 5 ) (4, 5) (4,5) 、 ( 3 , 6 ) (3, 6) (3,6) 和 ( 3 , 4 ) (3, 4) (3,4) 。
鲍勃想回到 B B B 单元格,卡罗尔想回到 C C C 单元格。他们都想沿着最短的路径走,也就是由尽可能少的单元格组成的路径。但是他们也想一起走。
如果鲍勃和卡罗尔各自走一条最短的路径回家,他们最多可以一起走多少个单元格?
1.Tutorial
主要思路就是判断B、C两个点关于A点的位置(A看成是原点,看B、C在第几象限),分情况讨论,讨论关于象限的位置,以及是否在同一坐标轴上
2.Solution
//https://codeforces.com/problemset/problem/1845/B
//00:39(+1)
//主要思路就是判断B、C两个点关于A点的位置(A看成是原点,看B、C在第几象限),分情况讨论,讨论关于象限的位置,以及是否在同一坐标轴上
#include最后:
每日一题系列旨在养成刷题的习惯,所以对代码的解释并不会特别详细,但足够引导大家写出来,选的题目都不会特别难,但也不是特别简单,比较考验大家的基础和应用能力,我希望能够将这个系列一直写下去,也希望大家能够和我一起坚持每天写代码。
之后每个星期都会不定期更新codeforces和atcoder上的题目,想要学习算法的友友们千万别错过了,有什么疑问欢迎大家在评论区留言或者私信博主!
在这里送大家一句话:广积粮,缓称王!