动态规划 | 鸡蛋问题 | 元旦假期来点“蛋”题

鸡蛋掉落 - 两枚鸡蛋

题目描述

原题链接

给你 2 枚相同 的鸡蛋，和一栋从第 1 层到第 n 层共有 n 层楼的建筑。

已知存在楼层 f ，满足 0 <= f <= n ，任何从 高于 f 的楼层落下的鸡蛋都 会碎 ，从 f 楼层或比它低 的楼层落下的鸡蛋都 不会碎 。

每次操作，你可以取一枚 没有碎 的鸡蛋并把它从任一楼层 x 扔下（满足 1 <= x <= n）。如果鸡蛋碎了，你就不能再次使用它。如果某枚鸡蛋扔下后没有摔碎，则可以在之后的操作中 重复使用 这枚鸡蛋。

请你计算并返回要确定 f 确切的值 的 最小操作次数 是多少？

动态规划解法

问题分析

状态定义：dp[i][j]表示总共有 i 层楼，现在手上有 j + 1 个鸡蛋。

状态计算：dp[i][1] = min(dp[i][1], max(j, dp[i - j][1] + 1))

我们假设总共有 i 层楼，从第 j 层楼往下扔第一个鸡蛋，有两种情况：

1. 鸡蛋碎了，那么说明f楼层一定小于j，即在第 j 层的楼下。此时的最少操作次数为j - 1 + 1 = j
2. 鸡蛋没碎，那么说明f楼层一定大于j，即在第 j 层的楼上。接下来，我们仍然持有 2 个鸡蛋，但此时考虑的楼层数只有i - j层。此时最少操作次数为dp[i - j][1] + 1

最终从第 j 层往下扔第一个鸡蛋，所需的最少操作次数为max(j, dp[i - j][1] + 1)

我们要做的就是遍历所有可能的情况j，找到所需操作次数最小的情况。

初始化：dp[i][0] = dp[i][1] = i

• 如果手上只有 1 个鸡蛋，i 层楼至少需要操作 i 次。
• 如果手上有 2 个鸡蛋，i 层楼的最少操作次数不超过 i 次。

程序代码

class Solution {
public:
    int twoEggDrop(int n) {
        vector<vector<int>> dp(n + 1, vector<int>(2, 0));
        // 初始化
        for(int i = 1; i <= n; i++) {
            dp[i][0] = i;
            dp[i][1] = i;
        }
        for(int i = 2; i <= n; i++) {
            for(int j = 1; j < i; j++) {
                dp[i][1] = min(dp[i][1], max(j, dp[i - j][1] + 1));
            }
        }
        return dp[n][1];
    }
};

观察上述代码，可以发现代码可以压缩成一维：

class Solution {
public:
    int twoEggDrop(int n) {
        vector<int> dp(n + 1);
        // 初始化
        for(int i = 1; i <= n; i++) {
            dp[i] = i;
        }
        for(int i = 2; i <= n; i++) {
            for(int j = 1; j < i; j++) {
                dp[i] = min(dp[i], max(j, dp[i - j] + 1));
            }
        }
        return dp[n];
    }
};

鸡蛋掉落

题目描述

原题链接

给你 k 枚相同的鸡蛋，并可以使用一栋从第 1 层到第 n 层共有 n 层楼的建筑。

已知存在楼层 f ，满足 0 <= f <= n ，任何从 高于 f 的楼层落下的鸡蛋都会碎，从 f 楼层或比它低的楼层落下的鸡蛋都不会破。

每次操作，你可以取一枚没有碎的鸡蛋并把它从任一楼层 x 扔下（满足 1 <= x <= n）。如果鸡蛋碎了，你就不能再次使用它。如果某枚鸡蛋扔下后没有摔碎，则可以在之后的操作中 重复使用 这枚鸡蛋。

请你计算并返回要确定 f 确切的值 的 最小操作次数 是多少？

问题分析

如果套用上一题的分析思路，我们可以定义如下状态以及状态计算。

状态定义：dp[i][j]表示总共有 i 层楼，现在手上有 j + 1 个鸡蛋。

状态计算：dp[i][k] = min(dp[i][k], max(dp[j-1][k-1] + 1, dp[i - j][k] + 1))，其中k表示手上有k + 1个鸡蛋，从第 j 层开始扔鸡蛋。

但是该方法最终会 TLE

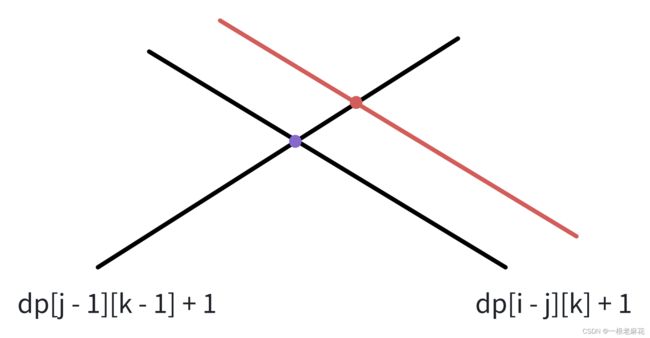
我们观察上述的状态转移方程，若我们固定鸡蛋的个数k + 1，可以发现，随着楼层数i的增加，dp[j-1][k-1] + 1这一项不会发生变动，即从第 j 层丢下的鸡蛋碎了。而dp[i - j][k] + 1这一项会随着楼层数i的增加而增加，即从第 j 层丢下的鸡蛋没碎。

接下来我们观察从第 j 层开始丢鸡蛋，随着j的增加，dp[j-1][k-1] + 1会逐渐增加，而dp[i - j][k] + 1会逐渐减小。而二者的交点位置就是dp[i][k]的最小值。

随着楼层数i的不断增加，dp[i - j][k] + 1不断上移动，而二者的交点也不断向右上方移动。

因此，当我们固定鸡蛋个数k+1时，随着楼层数i的不断增加，dp[i][j]最优解j的坐标也单调递增。

程序代码

class Solution {
public:
    int superEggDrop(int k, int n) {
        vector<int> dp(n + 1);
        // 初始化
        for(int i = 1; i <= n; i++) {
            dp[i] = i;
        }
        // 先固定鸡蛋个数
        for(int j = 2; j <= k; j++) {
            vector<int> f(n + 1);  // 存储从第x层丢下的鸡蛋没碎的历史最值
            int x = 1;  // 从第x楼开始抛
            f[0] = 0;
            // 总楼层数
            for(int i = 1; i <= n; i++) {
                while(x < i && max(dp[x-1], f[i - x]) >= max(dp[x], f[i - x -1])) {
                    x++;
                }
                f[i] = 1 + max(dp[x-1], f[i - x]);
            }
            for(int i = 1; i <= n; i++) {
                dp[i] = f[i];
            }
        }
        return dp[n];
    }
};

复杂度分析

时间复杂度为 $O(kn)$