算法专题五:位运算
算法专题五:位运算
- 一.常见位运算总结:
-
- 1.位1的个数
- 2.比特位记数
- 3.汉明距离
- 4.只出现一次的数字
- 5.只出现一次的数字三
- 二.判断字符是否为一
-
- 1.思路一:位运算思路
- GIF题目解析
- 三.丢失的数字
-
- 1.思路一:暴力思路
- 2.思路二:高斯求和思路:
- 3.思路三:哈希思路
- 4.思路四:位运算思路优化
- 四.两整数之和
-
- 1.思路一:按位异或+无进位相加
- 五.只出现一次的数字二
-
- 1.思路一:暴力思路+排序
- 2.思路二:异或思路:
- 六.消失的两个数字
-
- 1.思路一
一.常见位运算总结:
1.位1的个数
class Solution {
public:
int hammingWeight(uint32_t n) {
int count = 0;
for(int i=0;i<32;i++)
{
if((n>>i)&1)
count++;
//按位与& 有0就是0
//按位或| 有1就是1
//按位异或^ 相同为0相异为1
}
return count;
}
};
2.比特位记数
class Solution {
public:
vector<int> countBits(int n) {
vector<int> ans(n+1);
//1.考虑一趟扫描!
int hightbit = 0;
for(int i=1;i<=n;i++)
{
//1.判断是否需要更新数据:
if((i&(i-1)) == 0)
{
hightbit = i;
}
ans[i] = ans[i - hightbit]+1;
}
return ans;
}
};
3.汉明距离
1.通过提出每一位然后于1按位与提出x或者y的每一位数值。
2.进行判断是否相等不相等就count++;
class Solution {
public:
int hammingDistance(int x, int y) {
int count = 0;
for(int i=0 ; i<32 ; i++)
{
if (((x>>i) & 1) != ((y>>i) & 1))
count++;
}
return count;
}
};
4.只出现一次的数字
只出现一次的数字
1.一组数按位在一起按照题目意思只有一个数只有自己。
2.其他数值都是一对一对。
3.两个相同的数按位异或在一起结果是0
4.0和所有数按位异或在一起结果为那个数本身。
class Solution {
public:
int singleNumber(vector<int>& nums) {
int value = 0;
for(auto num:nums)
{
value^=num;
}
return value;
}
};
5.只出现一次的数字三
只出现一次的数字三
1.考虑特殊情况数组中只有两个元素直接返回这个数组。
2.排序:相同的数值一定相邻并且数组元素的个数为偶数。
3-1:特殊的两个数是相邻的–>指针移动长度
3-2:特殊的两个数是不是相邻的–>指针移动长度和边界控制问题!
class Solution {
public:
vector<int> singleNumber(vector<int>& nums) {
//0.特殊情况:
int n = nums.size();
if(n==2)
return nums;
//1.排序
sort(nums.begin(),nums.end());
//2.创建双指针分析各种情况解决方案:
int left = 0;
int right = 1;
vector<int> vv ;
while(left<n && right<=n)
{
//情况1: 1 1 2 3 3 4 4 5
if(right == n)
{
vv.push_back(nums[left]);
break;
}
if(nums[left]==nums[right])
{
left+=2;
right+=2;
}
else
{
vv.push_back(nums[left]);
left+=1;
right+=1;
}
}
return vv;
}
};
二.判断字符是否为一
1.思路一:位运算思路
class Solution {
public:
bool isUnique(string astr) {
int n = astr.size();
if(n > 26)
return false;
int bitmap = 0;
for(auto ch : astr)
{
int count = ch - 'a';
if(((bitmap>>count) & 1) == 1)
return false;
bitmap |= (1<<count);
}
return true;
}
};
GIF题目解析
三.丢失的数字
1.思路一:暴力思路
class Solution {
public:
int missingNumber(vector<int>& nums) {
int n = nums.size();
if(n == 1)
{
if(nums[0] == 1) return 0;
if(nums[0] == 0) return 1;
}
//1.排序:
sort(nums.begin() , nums.end());
//2.遍历找数:
for(int i=0 ; i < n ; i++)
{
if(i != nums[i])
return i;
}
return n;
}
};
//时间复杂度 1.排序:n*long^n 2. 遍历o(n)
//空间复杂度 O(1)
2.思路二:高斯求和思路:
class Solution {
public:
int missingNumber(vector<int>& nums) {
//1.求数组个数:
int n = nums.size();
//2.求从0到n的和
long long sum_1 = ((0+n)*(n+1))/2;
//3.遍历数组求和
long long sum_2 = 0;
for(auto num : nums)
{
sum_2 += num;
}
//4.计算结果:
return (sum_1 - sum_2);
}
};
//1.时间复杂度:O(n)
//2.空间复杂度为:O(1)
3.思路三:哈希思路
class Solution {
public:
int missingNumber(vector<int>& nums) {
//1.计算数组长度:
int n = nums.size();
//2.开一个哈希表
vector<int> hash(n+1);
//3.遍历数组第一遍给hash赋值:
for(auto num_1 : nums)
{
hash[num_1]++;
}
//4.遍历hash第一遍判断没有的返回出来:
for(int i=0 ; i < n+1 ;i++)
{
if (hash[i] == 0)
return i;
}
//照顾leetcode
return 0;
}
};
//时间复杂度:O(n)
//空间复杂度:O(n)
4.思路四:位运算思路优化
class Solution {
public:
int missingNumber(vector<int>& nums) {
//1.计算长度
int n = nums.size();
//2.异或所有数据:
int ret = 0;
for(int i=0 ; i<n ; i++)
{
ret^=nums[i];
}
for(int i=0 ; i<=n ;i++)
{
ret^=i;
}
return ret;
}
};
//时间复杂度:O(n)
//空间复杂度:O(1)
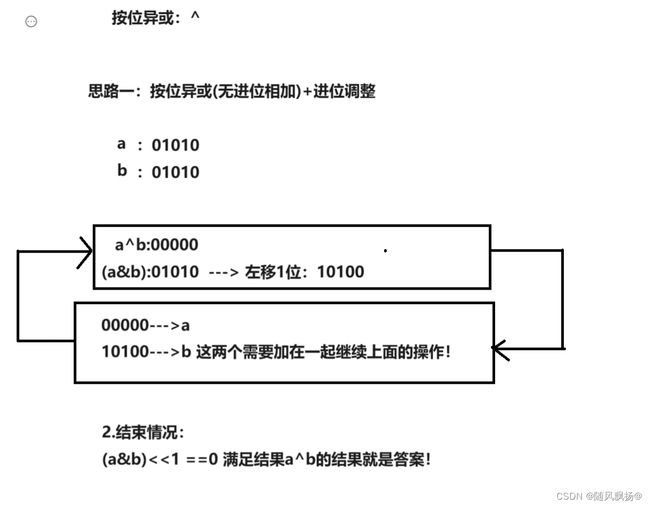
四.两整数之和
1.思路一:按位异或+无进位相加
class Solution {
public:
int getSum(int a, int b) {
while(((a&b)<<1)!=0)
{
//0.保存数据
int tmp = a;
//1.a的更新:
tmp = a^b;
//2.b的更新
b = ((a&b)<<1);
//3.数据归还
a = tmp;
}
return a^b;
}
};
五.只出现一次的数字二
只出现一次的数字二
1.思路一:暴力思路+排序
class Solution {
public:
int singleNumber(vector<int>& nums) {
if(nums.size()==1)
return nums[0];
//1.排序
sort(nums.begin(),nums.end());
//2.三指针遍历数据:
int l = 0;
int m = 1;
int r = 2;
while(l < nums.size())
{
if( m >= nums.size() && r >= nums.size())
{
return nums[l];
}
if(nums[m] == nums[r] && nums[m] != nums[l])
{
return nums[l];
}
else
{
l+=3;
m+=3;
r+=3;
}
}
return 0;
}
};
2.思路二:异或思路:
class Solution {
public:
int singleNumber(vector<int>& nums) {
int ret = 0;
for(int i=0;i<32;i++)
{
int sum = 0;
for(int x:nums)
{
if(((x>>i)&1) == 1)
sum++;
}
//推广到只出现n次的数组!
sum%=3;//3改变为n
if(sum == 1) ret |= (1<<i);
}
return ret;
}
};
//时间复杂度是:O(n)
//空间复杂度是:O(1)
六.消失的两个数字
1.思路一
class Solution {
public:
vector<int> missingTwo(vector<int>& nums) {
//1.异或所有数值:
int tmp = 0;
for(auto num:nums) tmp^=num;
for(int i=1 ; i<=nums.size()+2 ; i++) tmp ^=i;
//2.tmp==a^b;找出a,b中比特位不同的哪一位
int diff = 0;
while(1)
{
if(((tmp>>diff)&1) == 1) break;
else diff++;
}
//3.根据diff位置的不同把所有数据划分为两类去处理
int a = 0 , b = 0;
for(int x:nums)
if(((x>>diff) & 1) ==1 ) b^=x;
else a^=x;
for(int i=1;i<=nums.size()+2;i++)
if(((i>>diff)&1) == 1) b^=i;
else a^=i;
return {a,b};
}
};