文章解读与仿真程序复现思路——中国电机工程学报EI\CSCD\北大核心《考虑混合需求不确定性的电力-交通耦合网络最优定价策略》
本专栏栏目提供文章与程序复现思路,具体已有的论文与论文源程序可翻阅本博主的专栏栏目《论文与完整程序》
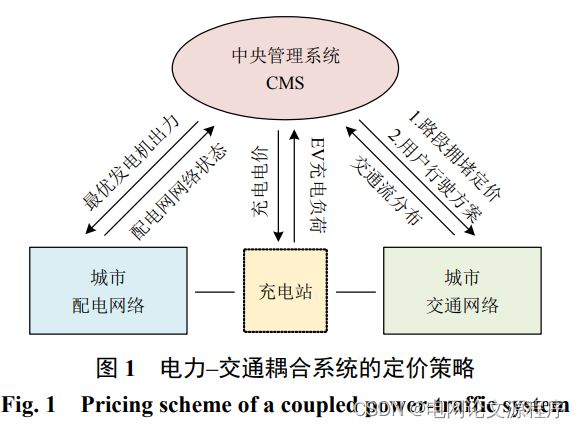
这个标题涉及到电力和交通两个领域的耦合网络以及在考虑混合需求不确定性情况下制定最优定价策略的问题。
首先,"电力-交通耦合网络"指的是电力系统和交通系统之间相互关联、相互影响的网络。电力系统提供能源,而交通系统则消耗这种能源。这种耦合可以体现在交通系统对能源的需求,以及电力系统对交通需求变化的响应上。
"混合需求不确定性"意味着存在多种类型的需求,并且这些需求在未来可能发生变化,但变化的趋势或幅度不确定。这可能涉及到不同类型的能源需求、交通需求、以及这些需求在不同时间段内的波动性或变化性。
最后,“最优定价策略”是指在这样一个电力-交通耦合网络中,针对不确定性的需求制定出的一种能够最大化效益或者最小化成本的价格策略。这种策略可能基于多种因素,如需求预测、资源供给、成本考量、环境因素等,以期望在考虑不确定性的情况下达到最优的经济效益和资源利用。
总体而言,这个标题所探讨的问题是如何在电力和交通两个耦合系统中,在面临多种需求不确定性的情况下,制定出最优的价格策略,以平衡能源供给与需求,并最大化效益。这可能涉及到复杂的数据分析、预测模型、优化算法以及对多种变量的综合考量。
摘要:随着电力网与交通网融合的不断加深,研究如何制定有效策略来优化整体系统具有重要意义。依托变分不等式,提出计及混合需求不确定性的电力–交通耦合网络最优定价策略,以引导系统在不确定风险下实现最优运行状态。首先研究了促进交通系统最优运行的路段拥堵收费策略,从理论上说明该策略能够引导和改变用户的行为,实现系统的最优运行状态。其次,提出耦合网络的最优定价模型,并推导其等价变分不等式形式。在此基础上,提出考虑混合需求不确定性的电力–交通耦合网络鲁棒定价模型及其等价变分不等式形式,从而将复杂鲁棒优化问题转化为变分不等式问题进行求解,为电力–交通耦合网络的复杂鲁棒优化问题提供新的解决思路。最后,仿真基于耦合测试系统,验证了所提方法的有效性。
这摘要涉及到随着电力网与交通网的融合,如何制定有效策略来优化整个系统,特别关注了在考虑混合需求不确定性的情况下的电力-交通耦合网络最优定价策略。
-
背景与意义: 随着电力网与交通网的融合加深,优化整体系统变得至关重要。此融合的背景下,制定有效策略对于引导系统在不确定风险下实现最优运行状态具有关键性意义。
-
方法和理论基础: 采用变分不等式的理论基础,提出了一种考虑混合需求不确定性的电力-交通耦合网络最优定价策略。首先,通过研究路段拥堵收费策略,理论上证明了这种策略可以引导和改变用户的行为,从而实现整个系统的最优运行状态。
-
模型提出与推导: 文中提出了耦合网络的最优定价模型,并推导了其等价的变分不等式形式。在此基础上,引入了混合需求不确定性,提出了相应的电力-交通耦合网络鲁棒定价模型,并推导了其等价的变分不等式形式。
-
求解思路: 通过将复杂鲁棒优化问题转化为变分不等式问题进行求解,为电力-交通耦合网络的复杂鲁棒优化问题提供了新的解决思路。
-
验证与实验: 最后,通过仿真基于耦合测试系统的实验,验证了所提出方法的有效性。这意味着提出的电力-交通耦合网络最优定价策略在实际应用中是可行且有效的。
综合来看,这篇论文致力于在电力和交通系统融合的背景下,提供了一种考虑混合需求不确定性的最优定价策略。通过理论论证和仿真实验,作者试图证明该策略的有效性,并提供了新的鲁棒优化问题解决思路。
关键词: 最优定价;变分不等式;电力-交通耦合网络;混合用户均衡;
-
最优定价(Optimal Pricing): 表示研究中关注的一个关键概念,即在给定条件下,通过制定合适的价格策略来达到最优化的目标。在这个上下文中,最优定价可能涉及到平衡供求关系、最大化效益、或者最小化成本。
-
变分不等式(Variational Inequality): 这是一种数学工具,用于描述不等式约束条件下的最优化问题。在该研究中,变分不等式可能被用于建模和解决电力-交通耦合网络中的优化问题,特别是在考虑混合需求不确定性的情况下。
-
电力-交通耦合网络(Power-Transportation Coupled Network): 涉及到电力系统和交通系统之间相互关联和相互影响的网络。这种耦合可能涉及到电力系统供能和交通系统对能源的需求之间的复杂关系。
-
混合用户均衡(Mixed User Equilibrium): 这可能是一个交通系统规划和管理中的概念,表示在系统中存在不同类型用户的均衡状态。"混合"可能指的是用户具有不同需求或特征,而"均衡"则表示在系统中达到了一种平衡状态,使得用户无法通过改变其策略而单方面改善自己的状态。
这些关键词的结合暗示了研究的主要内容,即在电力-交通耦合网络中,通过变分不等式方法研究最优定价策略,尤其是考虑到混合用户均衡的情况。这表明研究不仅关注于理论建模(变分不等式),还关注于实际系统中的优化问题(最优定价),并特别考虑了不同类型用户的影响。
仿真算例:
仿真测试系统采用文献[8]中的改进 Nguyen 交 通网和 IEEE 33 配电网,其拓扑结构见图 2。交通 需求对参数如表 1 所示(基准值设为 10),其表示交 通需求由起始点到终点的用户流量大小(通常由预 测获得)。其余路段容量、自由行驶时间、可行路径 等参数见文献[8]。对于配电网,功率基准为 10MV·A,线路电阻和电抗,节点基准负荷见文 献[15]。其余相关参数见表 2。为了对比分析,对 上述系统分别求解如下 3 种问题。案例 1:不考虑拥堵定价策略,两网互相作用 最终达到自发的平衡状态,即耦合网络均衡问题, 其具体变分不等式形式见文献[24]; 案例 2:考虑综合定价策略,耦合网络实现最 优运行,即 OPM 问题,等价于求解变分不等式问 题(见式(58)):VI(FRO, ΩRO)。 案例 3:考虑需求不确定性,耦合网络实现在 不确定场景下的最优运行,即 RPM 问题,等价于 求解变分不等式 VI(FRO, ΩRO)。 需指出,案例 2 的用户仍以个体利益选择出行 方案,中央管理系统并非直接控制用户行为,而是 通过价格来引导和改变用户均衡状态,故与案例 1 对比可说明价格策略的有效性。仿真中所有变分不 等式问题均使用改进投影–收缩算法[24]进行求解, 且所有算法相关参数均同文献[24]。
仿真程序复现思路:
复现上述仿真思路的步骤可以分为以下几个部分:
import networkx as nx
import numpy as np
def initialize_networks():
# 读取交通网络拓扑结构和参数
traffic_network = nx.read_edgelist("traffic_network.txt", nodetype=int, data=(("capacity", float), ("free_flow_time", float)))
# 读取配电网络拓扑结构和参数
power_network = nx.read_edgelist("power_network.txt", nodetype=int, data=(("resistance", float), ("reactance", float)))
return traffic_network, power_network
def initialize_parameters():
# 初始化仿真参数
traffic_demand = {edge: 10 for edge in traffic_network.edges()} # 基准值设为10
power_base_power = 10 # MV·A
# 其他相关参数设定
return traffic_demand, power_base_power
def solve_coupled_equilibrium(traffic_network, power_network, traffic_demand, power_base_power, algorithm_params):
# 求解耦合网络均衡问题
# 使用改进投影–收缩算法
# 具体实现略去
result_case1 = {} # 假设有一个结果对象
return result_case1
def solve_optimal_operation(traffic_network, power_network, traffic_demand, power_base_power, algorithm_params):
# 求解最优运行问题
# 使用改进投影–收缩算法
# 具体实现略去
result_case2 = {} # 假设有一个结果对象
return result_case2
def solve_uncertain_operation(traffic_network, power_network, traffic_demand, power_base_power, algorithm_params):
# 求解需求不确定性下的最优运行问题
# 使用改进投影–收缩算法
# 具体实现略去
result_case3 = {} # 假设有一个结果对象
return result_case3
def plot_results(result, case_name):
# 分析和可视化结果
# 使用 Matplotlib 或其他绘图库
# 具体实现略去
def main():
# 主程序
# 步骤1:准备工作
traffic_network, power_network = initialize_networks()
# 步骤2:设定仿真参数
traffic_demand, power_base_power = initialize_parameters()
# 步骤3:求解耦合网络均衡问题(案例1)
result_case1 = solve_coupled_equilibrium(traffic_network, power_network, traffic_demand, power_base_power, algorithm_params)
# 步骤4:求解最优运行问题(案例2)
result_case2 = solve_optimal_operation(traffic_network, power_network, traffic_demand, power_base_power, algorithm_params)
# 步骤5:求解需求不确定性下的最优运行问题(案例3)
result_case3 = solve_uncertain_operation(traffic_network, power_network, traffic_demand, power_base_power, algorithm_params)
# 步骤6:分析和比较结果
plot_results(result_case1, "Case 1")
plot_results(result_case2, "Case 2")
plot_results(result_case3, "Case 3")
# 展示图形
plt.show()
if __name__ == "__main__":
main()
在实际情况中,根据文献中的算法描述和相关方法,需要实现 solve_coupled_equilibrium、solve_optimal_operation 和 solve_uncertain_operation 函数,并根据实际需求进行参数设置和结果分析。此外,具体的网络拓扑文件、参数文件以及算法参数需要根据实际情况进行替换。