算法基础（快排 选择 归并 二分 高精度加减乘除 前缀和

一. 快速排序

1.先确定一个元素x（可为l ，r，（l+r）/2），作为后续递归比较的位置，还有两个指针分别指向数组两端。注意进入循环时需要分别扩大一位。

2.调整范围 左指针先向右移动，当遇上了大于x的元素时停下，此时右指针向左移动，当遇上了小于x的元素时停下，两元素swap交换，最后循环完两指针指向同一位置后，左边部分为小于x，右边部分为大于x。

3.分别递归左右两部分。

void quick_sort(int q[], int l, int r)
{
    if (l >= r) return;

    int i = l - 1, j = r + 1, x = q[(l + r )/2];
    while (i < j)
    {
        do i ++ ; while (q[i] < x);
        do j -- ; while (q[j] > x);
        if (i < j) swap(q[i], q[j]);
    }
    quick_sort(q, l, j), quick_sort(q, j + 1, r);
}

函数对数组进行操作，所以无需返回值

选择排序

形式一

与快排类似，但函数里参数为k值   int  fenzhi(int l,int r,int k)

因为最后返回值直接为第k个数，相当于无限递归夹击，找出第k个数               if(l==r) return q[l];

这里在一次while循环结束之后，就开始先判断第k个数是在左半边还是右半边，然后再对一边进行递归。

    int s=j-l+1;           （和形式2比起来这里确实每个部分中k是第几个没很大必要
    if(k<=s) return fenzhi(l,j,k);
    return fenzhi(j+1,r,k-s);

形式二

int quick_select(int l, int r)

if (k <= j) return quick_select(l, j);
    return quick_select(j + 1, r);

注意main（)函数里k--，因为这里k对应l=r时刻，所以数组下标为-1

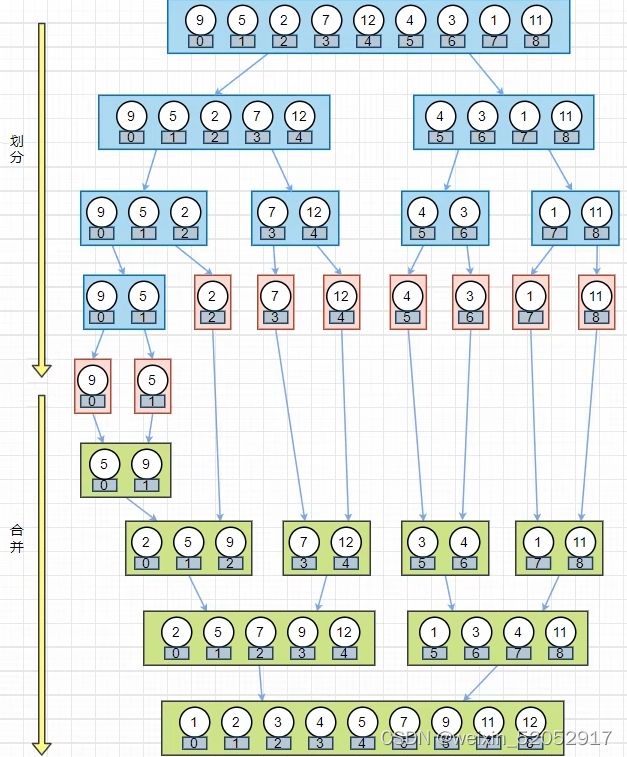
二.归并排序

1.确定分界点 mid=（l+r）/2

2.递归排序 左右两边

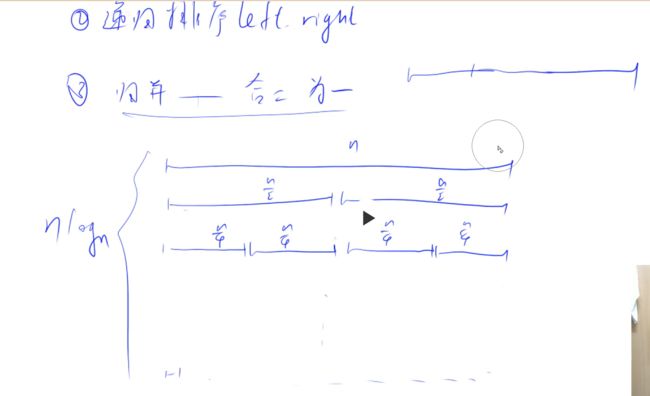
3.归并 合二为一

（选择排序和归并排序的时间复杂度:

void merge_sort(int q[], int l, int r)
{
    if (l >= r) return;

    int mid =（ l + r ）/2;
    merge_sort(q, l, mid);
    merge_sort(q, mid + 1, r);

    int k = 0, i = l, j = mid + 1;
    while (i <= mid && j <= r)
        if (q[i] <= q[j])   tmp[k ++ ] = q[i ++ ];
        else   tmp[k ++ ] = q[j ++ ];

    while (i <= mid) tmp[k ++ ] = q[i ++ ];
    while (j <= r) tmp[k ++ ] = q[j ++ ];

    for (i = l, j = 0; i <= r; i ++, j ++ ) q[i] = tmp[j];
}

递归原理：

逆序对数量

 if(l==r) return 0;    //如果无两个元素以上的数组，则无返回值
    int mid=(l+r)/2;
    res=nixu(q,l,mid)+nixu(q,mid+1,r);      //从这里开始递归到只剩一个元素的两个数组，然后才开始回溯下面的代码
    int k=0,i=l,j=mid+1;
    while(i<=mid && j<=r)
    {
        if(q[i]<=q[j]) temp[k++]=q[i++];
        else{
            res+=mid-i+1;  
            temp[k++]=q[j++] ;
               }
    }
    while(i<=mid) temp[k++]=q[i++];
    while(j<=r) temp[k++]=q[j++];

    for(int i=l,j=0;i<=r;i++,j++) q[i]=temp[j];
    return res;

二分

bool check(int x) {/* ... */} // 检查x是否满足某种性质

// 区间[l, r]被划分成[l, mid]和[mid + 1, r]时使用：
int bsearch_1(int l, int r)
{
    while (l < r)
    {
        int mid = l + r >> 1;
        if (check(mid)) r = mid;    // check()判断mid是否满足性质
        else l = mid + 1;
    }
    return l;
}
// 区间[l, r]被划分成[l, mid - 1]和[mid, r]时使用：
int bsearch_2(int l, int r)
{
    while (l < r)
    {
        int mid = l + r + 1 >> 1;
        if (check(mid)) l = mid;
        else r = mid - 1;
    }
    return l;
}

高精度加减乘除

一 高精度加法

首先这里因为是高精度的两个数相加，所以我们用vector来存两个数。

先利用string函数来读入两个字符串a，b对应高精度的数A、B，因为我们要从个位开始相加，所有此时逆序两个数来算更方便。

由于string a，b是字符串类型，所以我们需要转化成为数字相加减，既是a[i]-'0'，两个字符串转化完成之后传入加法函数。

因为我们此时A，B都是逆序，个位在前，所以正向循环相加，设置一个变量t，分别加AB对应位置的数，然后%10存入最后要返回的容器C,再/10表示是否有进位，直到有两个数都遍历完了则跳出循环，判断最后一位相加是否有进位。

最后main函数里逆向输出即可

二 高精度减法

和高精度加法的区别在于：需要判断负号的情况，和进位的细节

负号可以用一个bool函数来return A>B的情况，再在main函数里添加负号即可

这里进位的方法是 利用一个变量t，来传递每个A[i]，t=A[i]-t，只要B[i]没循环完，则t每次减去B[i]，再将减完之后的t，返回到C中的(t+10)%10,然后下一步判断减完之后的t是否小于0，如果是的，说明需要进位，则返回t=1，反之返回t=0。最后记得去除前导0

三 高精度乘法

高精度乘法需要注意的是，一个高精度数，一个int型，可直接利用高精度每一位去直接*int型，然后%10取得当下这位的数存进C中，再/10既是需要的进位，加到下一个循环中。注意循环的结束条件不仅仅是循环A[i]中每一位，还有最后t的进位也需要加进C中。最后注意去除前导0即可。

四 高精度除法

除法需要注意的是从后往前遍历，因为是位数高的地方开始除，设置一个变量r来保存每次相除的余数，余数*10+下一位为 下一个 被除数，然后再除b放入C中。

需要注意的是此时C是正序的，所以利用reverse函数逆序之后再来去除前导0。

前缀和

用来随意算数组中l~r之和

S[n]=S[n-1]+an;

S[r]-S[l-1]   l~r之和

二维前缀和