分层图总结

分层图定义

分层图，顾名思义，是许多张图一层一层堆叠在同一维度内。如果把一张普通的图定位一层楼，那么分层图就是由许多层楼叠起来的一栋楼。而连接每一层图的边，就相当于一栋楼里的楼梯。

那么，分层图一般用来干什么呢？？

当我们遇到这类题：

给你n个点，m条边，每条边都有边权。现在你可以任意选择k条边，使它的边权为0。问从起点到终点的最短路。

在这时，我们就可以通过构建分层图来求解。具体见下文。

分层图实现

分层图的实现主要就难在建图，剩余的就和普通的图没什么区别了。

分层图建图

个人认为，分层图建图的思想类似于扩展域并查集，即：假设一共要建$k$层图，那么我们就开一个$k\times n$的数组，每$n$个位置存一层图的点，一共分$k$层。具体见下图：

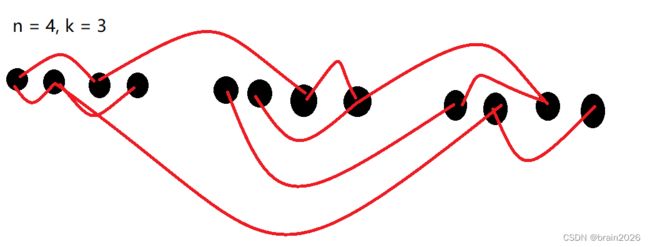
此时，第$i$层的点的下标为$1+(i-1)\times n\sim n+(i-1)\times n$。具体见图见$code$：

for(int i = 1; i <= m; i ++) {
		int x, y, z;
		scanf("%d%d%d", &x, &y, &z);
		add(x, y, z);
		add(y, x, z);
		for(int j = 1; j <= k; j ++) {//除了第一层以外要建k层图
			add(x + j * n, y + j * n, z);//第k层图里的边
			add(y + j * n, x + j * n, z);
			add(x + (j - 1) * n, y + j * n, 0);//连接两层图之间的边
			add(y + (j - 1) * n, x + j * n, 0);//注意连接层与层之间的边是单向边
		}
	}

分层图最短路

图建好后，剩下的就是正常的跑最短路了。但是，有一点需要注意：不见得最优答案会产生在第k层图中。也就是，不见得会跑到第k层图中。

什么时候会出现这种情况呢？当$m<k$的时候。假设$m=1,k=10$，我们只有一条边，也就是说，我们最多建两层图。那么遇到这种情况该怎么办呢？

1. 可以在每一层的终点处向下一层的终点处连一条边
2. 可以在统计答案的时候在每一层中取最小值

两种方法任选即可。

具体见例题。

分层图例题

luogu P4568 飞行路线

板子题，套代码即可。

$ACcode$：

#include
using namespace std;

const int maxn = 1e4 + 5;
const int maxm = 5e4 + 5;
int n, m, k, s, t;
struct my_str {
  int to, nxt, val;
}edge[maxm * 50];
int head[maxn * 20], tot = 0;
int dis[maxn * 20];
bool vis[maxn * 20];
struct my_str2 {
  int loc, road;
  friend bool operator <(my_str2 a, my_str2 b) {
    return a.road > b.road;
  }
};
priority_queue < my_str2 > qq;

void add(int x, int y, int z) {
  edge[++ tot] = (my_str){y, head[x], z};
  head[x] = tot;
}

inline int read() {
  int x = 0, f = 1;
  char ch = getchar();
  while(!isdigit(ch)) {
    if(ch == '-') f = -1;
    ch = getchar();
  }
  while(isdigit(ch)) {
    x = (x << 1) + (x << 3) + (ch ^ 48);
    ch = getchar();
  }
  return x * f;
}

void Dij() {//堆优化Dij
  memset(dis, 0x7f, sizeof dis);
  dis[s] = 0;
  qq.push((my_str2){s, 0});
  while(!qq.empty()) {
    int Loc = qq.top().loc;
    qq.pop();
    if(vis[Loc]) continue;
    vis[Loc] = 1;
    for(int i = head[Loc]; i != -1; i = edge[i].nxt) {
      int To = edge[i].to;
      int Val = edge[i].val;
      if(dis[To] > dis[Loc] + Val) {
        dis[To] = dis[Loc] + Val;
        qq.push((my_str2){To, dis[To]});
      }
    }
  }
}

int main() {
  n = read(), m = read(), k = read();
  s = read(), t = read();
  memset(head, -1, sizeof head);
  for(int i = 1; i <= m; i ++) {
    int x, y, z;
    x = read(), y = read(), z = read();
    add(x, y, z);
    add(y, x, z);
    for(int j = 1; j <= k; j ++) {
      add(x + j * n, y + j * n, z);
      add(y + j * n, x + j * n, z);
      add(x + (j - 1) * n, y + j * n, 0);
      add(y + (j - 1) * n, x + j * n, 0);
    }
  }
  Dij();
  int ans = 0x7f7f7f7f;
  for(int i = 0; i <= k; i ++) ans = min(ans, dis[t + i * n]);//统计每一层的答案
  printf("%d", ans);
  return 0;
}

板子题推荐：
luogu P2939 Revamping Trails G

luogu P4822 冻结