模拟集成电路笔记 | 第四部分 | Chapter 7
模拟集成电路笔记 | 第四部分 | Chapter 7
如想获得更好的阅读体验,可以访问以下链接:CMOS模拟集成电路-04
第七章 噪声
7.1 噪声的统计特性
-
平均“电压功率”概念
P a v = lim T → ∞ 1 T ∫ − T / 2 + T / 2 x 2 ( t ) d t P_{av}=\lim_{T\rightarrow \infty} \frac{1}{T}\int_{-T/2}^{+T/2}{x^2}(t)\mathrm{d}t Pav=T→∞limT1∫−T/2+T/2x2(t)dt本书的量纲是 V2 ,不是传统功率的 W = V 2 R W= \frac{V^2}{R} W=RV2 ,目的是为了方便观察
-
单边谱和双边谱
对于实数 x ( t ) x(t) x(t), S X ( f ) S_X(f) SX(f) 是 f f f 的偶函数
P a v = lim T → ∞ 1 T ∫ − T / 2 + T / 2 x 2 ( t ) d t 任何信号 x ( t ) = cos ω t 可化为 → 1 2 [ e j ω t + e − j ω t ] (把 ω 看成 f ,即信号从时域变换到 + f 和 − f ) P_{av}=\lim_{T\rightarrow \infty} \frac{1}{T}\int_{-T/2}^{+T/2}{x^2}(t)\mathrm{d}t \\ \text{任何信号} x\left( t \right) =\cos \omega t\,\,\underrightarrow{\text{可化为}}\,\,\frac{1}{2}\left[ e^{j\omega t}+e^{-j\omega t} \right] \\ \text{(把} \omega \,\,\text{看成} f\text{,即信号从时域变换到}+f\text{和}-f\text{)} Pav=T→∞limT1∫−T/2+T/2x2(t)dt任何信号x(t)=cosωt可化为21[ejωt+e−jωt](把ω看成f,即信号从时域变换到+f和−f)
7.2 噪声类型
7.2.1 热噪声
-
电阻热噪声
电阻热噪声可以⽤⼀个串联的电压源来模拟,电阻热噪声的功率谱密度:
S v ( f ) = 4 k T R , f ⩾ 0 S_{v}(f)=4 k T R, f \geqslant 0 Sv(f)=4kTR,f⩾0S v ( f ) S_{v}(f) Sv(f)也可以写成 V n 2 ‾ \overline{{V_n}^2} Vn2 ,量纲为 V 2 / H z V^2/Hz V2/Hz
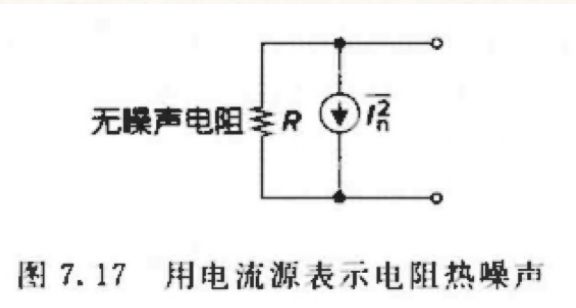
或者用并联的电流源模型表示:
I n 2 ‾ = 4 k T / R (量纲为 A 2 / H z ) \overline{I_{n}^{2}}=4kT/R\text{(量纲为}A^2/Hz\text{)} In2=4kT/R(量纲为A2/Hz) -
MOS 管上的噪声
-
沟道电流热噪声
工作在饱和区的长沟道MOS器件产生沟道噪声
I n 2 = 4 k T γ g m I_{\mathrm{n}}^{2}=4 k T \gamma \mathrm{g}_{\mathrm{m}} In2=4kTγgm这里的 γ \gamma γ 不是体效应系数,如果需要转化为等效电压 V n 2 ‾ \overline{{V_n}^2} Vn2,需要求解 I n 2 ‾ \overline{{I_n}^2} In2两侧阻抗 R R R, V n 2 ‾ = I n 2 ‾ R 2 \overline{V_{n}^{2}}=\overline{I_{n}^{2}}R^2 Vn2=In2R2
-
栅极电阻热噪声(与版图有关,略)
-
7.2.2 闪烁噪声或 1 f \frac{1}{f} f1 噪声
-
产生原因:MOS晶体管的栅氧化层和硅衬底界面出现许多“悬挂”键,载流子运动到这个界面时,有⼀些被随机地俘获,然后再被释放,从而产⽣了“闪烁”噪声。
V n 2 ‾ = K C o x W L 1 f \overline{V_{\mathrm{n}}^{2}}=\frac{K}{C_{\mathrm{ox}} W L} \frac{1}{f} Vn2=CoxWLKf1闪烁噪声用与栅串联电压源等效
-
转角频率
沟道电流热噪声= 1 / f 1/f 1/f 噪声时对应的频率 f c f_c fc
4 k T γ g m = K C o x W L 1 f c g m 2 f c = K γ C o x W L g m 1 4 k T 4kT\gamma g_m=\frac{K}{C_{ox}WL}\frac{1}{f_{\mathrm{c}}}g_{\mathrm{m}}^{2} \\ f_{\mathrm{c}}=\frac{K}{\gamma C_{\mathrm{ox}}WL}g_{\mathrm{m}}\frac{1}{4kT} 4kTγgm=CoxWLKfc1gm2fc=γCoxWLKgm4kT1
7.3 电路中的噪声表示
-
输出噪声
将输⼊置零,计算各噪声源在输出产⽣的总噪声
-
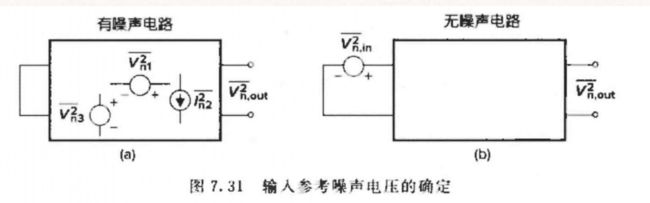
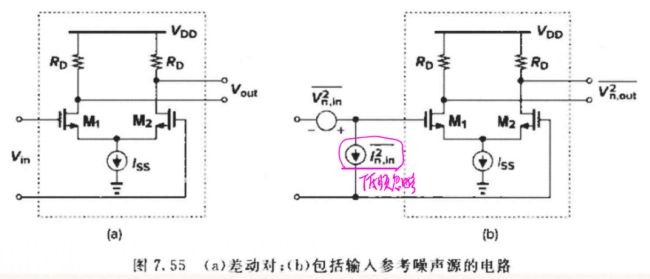
输入参考噪声
在输入端用一个信号源 V n , i n 2 ‾ \overline{V_{n,in}^{2}} Vn,in2 代表电路中所有的噪声源的影响。
先算出输出噪声功率 V n , o u t 2 ‾ \overline{V_{n,out}^{2}} Vn,out2,再得到 V n , i n 2 ‾ = V n , o u t 2 ‾ A v 2 \overline{V_{n,in}^{2}} = \frac{\overline{V_{n,out}^{2}}}{A_v^2} Vn,in2=Av2Vn,out2
-
当考虑前级电路时,即存在有限前级输出电阻时,输入参考噪声会减小。
当信号源 R 1 = 0 R_1 = 0 R1=0,或者MOS输入阻抗无穷大,一个电压源的模型才正确
方法:
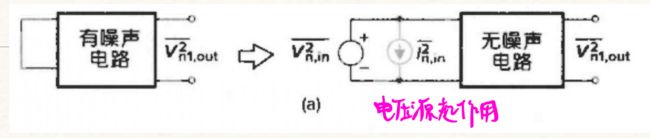
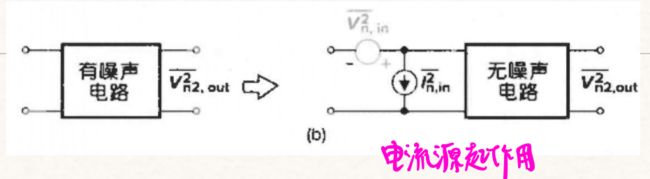
用电压源 V n , i n 2 ‾ \overline{V_{n,in}^{2}} Vn,in2 和电流源 I n , i n 2 ‾ \overline{I_{n,in}^{2}} In,in2 共同表示噪声
-
当输入短路(信号源阻抗为零)时:
-
当输⼊开路(信号源阻抗为⽆穷⼤)时:
-
-
7.4 单极放大器中的噪声
7.4.1 共源级
-
一般共源级
- 电阻 R D R_D RD 热噪声 I n 2 ‾ = 4 k T R D / V n 2 ‾ = 4 k T R D \overline{I_{n}^{2}}=\frac{4kT}{R_D}/\overline{V_{n}^{2}}=4kTR_D In2=RD4kT/Vn2=4kTRD
- 沟道电流热噪声 I n 2 ‾ = 4 k T γ g m \overline{I_{n}^{2}}=4kT\gamma g_m In2=4kTγgm
- 闪烁噪声 V n 2 ‾ = K C o x W L 1 f \overline{V_{n}^{2}}=\frac{K}{C_{ox}WL}\frac{1}{f} Vn2=CoxWLKf1
输入参考噪声电压: V n , i n 2 ‾ = 4 k T ( γ g m + 1 g m 2 R D ) + K C o x W L 1 f (计算一个噪声源时,需将其他噪声源和输入屏蔽) \text{输入参考噪声电压:}\overline{V_{n,in}^{2}}=4kT\left( \frac{\gamma}{g_{\mathrm{m}}}+\frac{1}{g_{\mathrm{m}}^{2}R_{\mathrm{D}}} \right) +\frac{K}{C_{ox}WL}\frac{1}{f} \\ \text{(计算一个噪声源时,需将其他噪声源和输入屏蔽)} 输入参考噪声电压:Vn,in2=4kT(gmγ+gm2RD1)+CoxWLKf1(计算一个噪声源时,需将其他噪声源和输入屏蔽)
计算如下:
1. 电阻 R D 热噪声 V n , o u t 2 ‾ = 4 k T R D ⋅ R o u t 2 , V n , i n 2 ‾ = 4 k T R D R o u t 2 ( ρ m R o u t ) 2 = 4 k T R 0 ρ m 2 2. 沟道电流热噪声 V n , o u t 2 ‾ = 4 k T y ρ m ⋅ R o u t , 2 , V n , i n 2 ‾ = 4 k T Y ρ m ⋅ R o u t 2 ( ρ m R o u t ) 2 = 4 k T y ρ m 3. 闪烁噪声 V n 2 ‾ = K C o x W L 1 f = V n , i n 2 ‾ (已经等效到晶体管栅级) 1.\text{电阻}R_D\text{热噪声} \overline{V_{n, \mathrm{out}}^{2}}=\frac{4kT}{R_D}\cdot R_{\mathrm{out}}^{2},\overline{V_{n, \mathrm{in}}^{2}}=\frac{4kT}{R_D}\frac{R_{\mathrm{out}}^{2}}{\left( \rho _mR_{\mathrm{out}} \right) ^2}=\frac{4kT}{R_0\rho _{m}^{2}} \\ 2.\text{沟道电流热噪声} \overline{V_{n, \mathrm{out}}^{2}}=4kTy\rho _m\cdot R_{\mathrm{out},}^{2},\overline{V_{n, \mathrm{in}}^{2}}=\frac{4kTY\rho _m\cdot R_{\mathrm{out}}^{2}}{\left( \rho _mR_{\mathrm{out}} \right) ^2}=\frac{4kTy}{\rho _m} \\ 3.\text{闪烁噪声} \overline{V_{n}^{2}}=\frac{K}{\,\,\mathrm{C}_{\mathrm{ox}}\mathrm{WL}}\frac{1}{f}=\overline{V_{n, \mathrm{in}}^{2}}\text{(已经等效到晶体管栅级)} 1.电阻RD热噪声Vn,out2=RD4kT⋅Rout2,Vn,in2=RD4kT(ρmRout)2Rout2=R0ρm24kT2.沟道电流热噪声Vn,out2=4kTyρm⋅Rout,2,Vn,in2=(ρmRout)24kTYρm⋅Rout2=ρm4kTy3.闪烁噪声Vn2=CoxWLKf1=Vn,in2(已经等效到晶体管栅级) -
有源负载的共源级
V n , o u t 2 ‾ = 4 k T ( γ g m 1 + γ g m 2 ) ( r o 1 ∥ r o 2 ) 2 (仅考虑了沟道电流热噪声) \overline{V_{\mathrm{n}, out\,\,}^{2}}=4kT\left( \gamma g_{m1}+\gamma g_{m2} \right) \left( r_{o1}\parallel r_{o2} \right) ^2 \\ \text{(仅考虑了沟道电流热噪声)} Vn,out2=4kT(γgm1+γgm2)(ro1∥ro2)2(仅考虑了沟道电流热噪声)
-
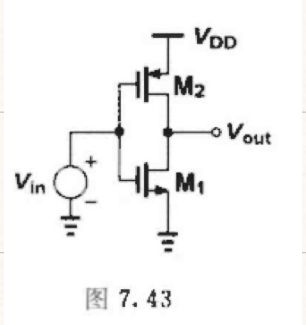
互补共源级
V n , i n 2 ‾ = 4 k T γ g m 1 + g m 2 \overline{V_{\mathrm{n}, \mathrm{in}}^{2}}=\frac{4 k T \gamma}{g_{\mathrm{m} 1}+g_{\mathrm{m} 2}} Vn,in2=gm1+gm24kTγ
7.4.2 共栅极
由于共栅级输⼊阻抗较低,需要考虑输⼊参考噪声电流
-
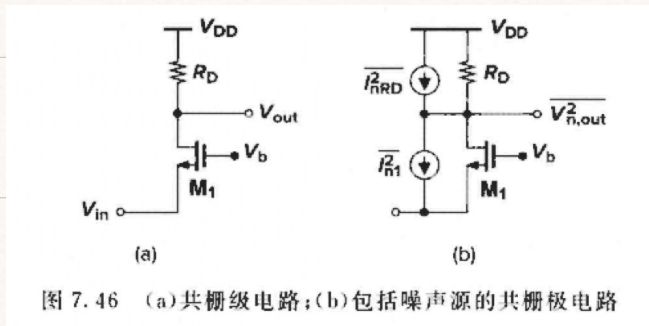
一般共栅极
-
当输入短路时:
( 4 k T γ g m + 4 k T R n ) R D 2 ⏟ 图 a = V n , i n 2 ‾ ( g m + g m b ) 2 R D 2 ⏟ 图 b V n , i n 2 ‾ = 4 k T ( γ g m + 1 / R D ) ( g m + g m b ) 2 \underset{\text{图}a}{\underbrace{\left( 4kT\gamma g_m+\frac{4kT}{R_{\mathrm{n}}} \right) R_{\mathrm{D}}^{2}}}=\underset{\text{图}b}{\underbrace{\overline{V_{\mathrm{n},\mathrm{in}}^{2}}\left( g_{\mathrm{m}}+g_{mb} \right) ^2R_{\mathrm{D}}^{2}}} \\ \overline{V_{n, \mathrm{in}}^{2}}=\frac{4kT\left( \gamma g_m+1/R_D \right)}{\left( g_m+g_{mb} \right) ^2} 图a (4kTγgm+Rn4kT)RD2=图b Vn,in2(gm+gmb)2RD2Vn,in2=(gm+gmb)24kT(γgm+1/RD)
-
当输入开路时:
因为输⼊开路, I n 1 + I D 1 = 0 I_{n1}+ I_{D1}= 0 In1+ID1=0,⽽⽆M1 输出的噪声电流
V n 2 , o u t 2 ‾ = I n R D 2 ‾ R D 2 = 4 k T R D ( 图 c ) I n , i n 2 ‾ R D 2 = V n 2 , o u t 2 ‾ (图 d ) 联立可得: I n , b 2 ‾ = 4 k T R D \overline{V_{n2, \mathrm{out}}^{2}}=\overline{I_{nRD}^{2}}R_{D}^{2}=4kTR_D\quad \left( \text{图}c \right) \\ \overline{I_{n, \mathrm{in}}^{2}}R_{D}^{2}=\overline{V_{n2,\mathrm{out}}^{2}}\text{(图}d\text{)} \\ \text{联立可得:} \overline{I_{\mathrm{n},\mathrm{b}}^{2}}=\frac{4kT}{R_{\mathrm{D}}} Vn2,out2=InRD2RD2=4kTRD(图c)In,in2RD2=Vn2,out2(图d)联立可得:In,b2=RD4kT
-
-
带偏置电流源的CG (Common Gate)
-
当输入短路时
In2 不流过 RD,对输入参考电压的计算没有贡献,计算过程同⼀般 CG 输入短路时情况
-
当输⼊开路时
把 M1 看成⼀个⿊匣⼦,噪声电流 In1 和漏电流 ID1 内循环,对输出噪声电压⽆贡献得到 M2 沟道电流热噪声对输出噪声电压贡献为: I n 2 2 ‾ R D 2 \overline{I_{n 2}^{2}} R_{D}^{2} In22RD2
在计算总输出噪声电压时还应该加上电阻 RD 的热噪声贡献
-
-
闪烁噪声
输⼊阻抗低,需考虑输⼊参考噪声电流模型
-
输⼊接地时,M2的闪烁噪声对输出⽆影响
$$
\overline{V_{n, \mathrm{out}}^{2}}=\frac{1}{C_{\mathrm{ox}}f}\left[ \frac{g_{\mathrm{m}1}{2}K_{\mathrm{N}}}{(WL)_1}+\frac{g_{\mathrm{m}3}{2}K_{\mathrm{p}}}{(WL)3} \right] \left( r{o1}\parallel r_{o3} \right) ^2
\
\text{其中上式中}M_1\text{的}1/f\text{噪声为:}\frac{g_{\mathrm{m}1}^{2}K_{\mathrm{N}}}{(WL)1}, M_3\text{的}1/f\text{噪声为:}\frac{g{\mathrm{m}3}^{2}K_{\mathrm{p}}}{(WL)3}.
\
\text{闪烁噪声}\overline{V{n,,}^{2}}=\frac{K}{C_{ox}WL}\frac{1}{f}
\\
\overline{V_{n, in,,}^{2}}=\frac{1}{C_{\mathrm{ox}}f}\left[ \frac{K_Pg_{\mathrm{m}3}{2}}{(WL)_3}+\frac{K_Ng_{\mathrm{m}1}{2}}{(WL)1} \right] \frac{1}{\left( g{\mathrm{m}1}+g_{\mathrm{mbl}} \right) ^2}
\
\text{增益为}:\left( g_{m1}+g_{mb1} \right) \left( r_{o1}\parallel r_{o2} \right)
$$ -
输⼊开路时,M1的闪烁噪声对输出⽆影响
V n , o u t 2 ‾ = 1 C o x f [ K P g m , 3 2 ( W L ) 3 + K N g m 2 2 ( W L ) 2 ] R o u t 2 I n , i n 2 ‾ = 1 C o x f [ K P g m 3 2 ( W L ) 3 + K N g m 2 2 ( W L ) 2 ] \begin{aligned} &\overline{V_{n,out}^{2}}\,\,=\frac{1}{C_{\mathrm{ox}}f}\left[ \frac{K_{\mathrm{P}}g_{\mathrm{m},3}^{2}}{(WL)_3}+\frac{K_Ng_{\mathrm{m}2}^{2}}{(WL)_2} \right] R_{\mathrm{out}}^{2}\\ &\overline{I_{\mathrm{n},in\,\,}^{2}}=\frac{1}{C_{\mathrm{ox}}f}\left[ \frac{K_{\mathrm{P}}g_{\mathrm{m}3}^{2}}{(WL)_3}+\frac{K_{\mathrm{N}}g_{\mathrm{m}2}^{2}}{(WL)_2} \right]\\ \end{aligned} Vn,out2=Coxf1[(WL)3KPgm,32+(WL)2KNgm22]Rout2In,in2=Coxf1[(WL)3KPgm32+(WL)2KNgm22]
-
7.4.3 源跟随器
V n , i n 2 ‾ = V n 1 2 ‾ + V n , o u t 2 ‾ ∣ M 2 A v 2 = 4 k T γ ( 1 g m 1 + g m 2 g m l 2 ) \begin{aligned} &\overline{V_{n,in}^{2}}=\overline{V_{n1}^{2}}+\frac{\left. \overline{V_{\mathrm{n},out}^{2}} \right|_{M_2}}{A_{v}^{2}} =4kT\gamma \left( \frac{1}{g_{\mathrm{m}1}}+\frac{g_{\mathrm{m}2}}{g_{\mathrm{ml}}^{2}} \right)\\ \end{aligned} Vn,in2=Vn12+Av2Vn,out2∣ ∣M2=4kTγ(gm11+gml2gm2)
V n , o u t 2 ‾ ∣ M 2 = I n 2 2 ‾ ( 1 g m 1 ∥ 1 g m b 1 ∥ r o 1 ∥ r o 2 ) 2 A v = 1 g m b 1 ∥ r o 1 ∥ r o 2 1 g m b 1 ∥ r o 1 ∥ r o 2 + 1 g m 1 \begin{aligned} &\left. \overline{V_{n, out\,\,}^{2}} \right|_{\mathrm{M}_2}=\overline{I_{\mathrm{n}2}^{2}}\left( \frac{1}{g_{\mathrm{m}1}}\left\| \frac{1}{g_{\mathrm{mb}1}} \right\| r_{o1}\parallel r_{o2} \right) ^2\\ &A_v=\frac{\frac{1}{g_{mb1}}\left\| r_{o1} \right\| r_{o2}}{\frac{1}{g_{mb1}}\left\| r_{o1} \right\| r_{o2}+\frac{1}{g_{m1}}}\\ \end{aligned} Vn,out2∣ ∣M2=In22(gm11∥ ∥gmb11∥ ∥ro1∥ro2)2Av=gmb11∥ro1∥ro2+gm11gmb11∥ro1∥ro2
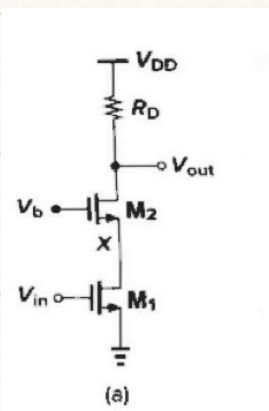
7.4.4 共源共栅级
V n , i n 2 ‾ ∣ M 1 ⋅ R D = 4 k T ( γ g m l + 1 g m 1 2 R D ) \left. \overline{V_{n, \mathrm{in}}^{2}} \right|_{M_1\cdot R_{\mathrm{D}}}=4kT\left( \frac{\gamma}{g_{\mathrm{m}\mathbf{l}}}+\frac{1}{g_{\mathrm{m}1}^{2}R_{\mathrm{D}}} \right) Vn,in2∣ ∣M1⋅RD=4kT(gmlγ+gm12RD1)
⾼频时噪声增加,低频时由于Cascode 隔离噪声作⽤可忽略
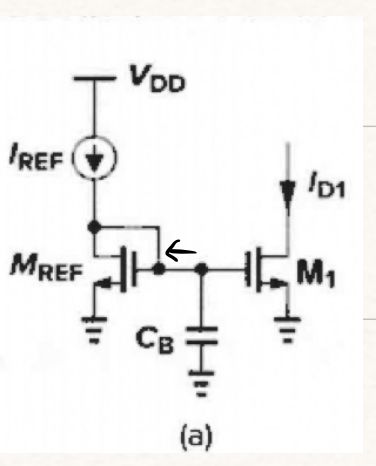
7.5 电流镜中的噪声
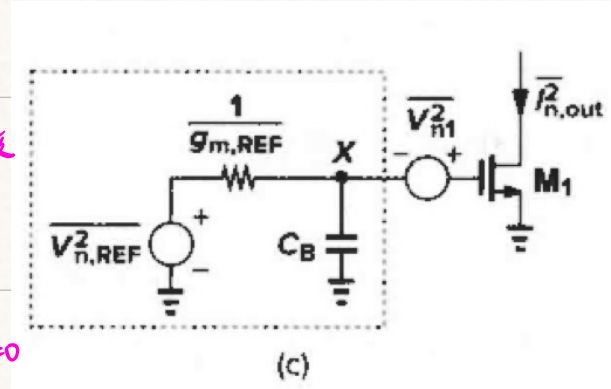
对 MREF 的闪烁噪声构建戴维南等效,得到以下:
1️⃣计算开路电压,因为 IREF 恒定不变,VGS,REF 不变,即 V 1 = 0 V_1 = 0 V1=0 ,得到开路电压为 V n , R E F 2 ‾ \overline{V_{n,REF}^{2}} Vn,REF2 ;
2️⃣计算开路电阻,把 IREF 看成开路,此时 V 1 ≠ 0 V_1 \ne 0 V1=0,得开路电阻为 1 g m , R E F \frac{1}{g_{m,REF}} gm,REF1。
得到以下:
输出噪声电流:$
\overline{I_{n,out}^{2}}=\left( \frac{g_{\mathrm{m},\mathrm{REF}}{2}}{C_{B}{2}\omega 2+g_{\mathrm{m},\mathrm{REF}}{2}}\overline{V_{n,REF}{2}}+\overline{V_{n1}{2}} \right) g_{\mathrm{m}1}^{2}
$
7.6 差动对中的噪声
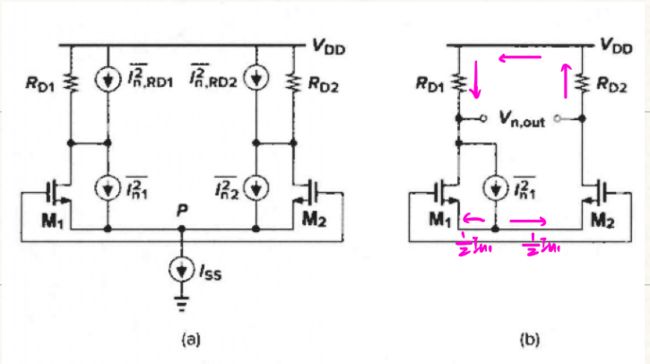
(a) 输入短接( V n , i n 2 ‾ = 0 \overline{V_{n,in}^{2}} = 0 Vn,in2=0 的意思?),画出各噪声源
(b) 考虑单噪声源 I n 1 2 ‾ \overline{I_{n1}^{2}} In12 的情况,从M1, M2 源极看进去的阻抗大小一样,即有 I n 1 2 ‾ \overline{I_{n1}^{2}} In12 被均分
V n , o u t ∣ M 1 = I n l 2 R D 1 + I n 1 2 R D 2 (方向不清楚怎么确定) V n , o u t 2 ‾ ∣ M 1 ⋅ M 2 = ( I n 1 2 ‾ + I n 2 2 ‾ ) R D 2 ( R D 1 = R D 2 = R D ) \left. V_{n,out} \right|_{M_1}=\frac{I_{n\mathrm{l}}}{2}R_{D1}+\frac{I_{n1}}{2}R_{D2}\text{(方向不清楚怎么确定)} \\ \left. \overline{V_{n,out\,\,}^{2}} \right|_{M_1\cdot M_2}=\left( \overline{I_{\mathrm{n}1}^{2}}+\overline{I_{\mathrm{n}2}^{2}} \right) R_{\mathrm{D}}^{2}\text{(}R_{D1}=R_{D2}=R_D\text{)} Vn,out∣M1=2InlRD1+2In1RD2(方向不清楚怎么确定)Vn,out2∣ ∣M1⋅M2=(In12+In22)RD2(RD1=RD2=RD)
V n , o u t 2 ‾ = ( V n , o u t 2 ‾ + V n , o u t 2 ‾ ) R D 2 + 2 ( 4 k T R D ) = 8 k T ( γ g m R D 2 + R D ) \begin{aligned} \overline{V_{n,out\,\,}^{2}}&=\left( \overline{V_{n,out\,\,}^{2}}+\overline{V_{n,out\,\,}^{2}} \right) R_{D}^{2}+2\left( 4kTR_D \right) \\ &=8kT\left( {\gamma _g}_mR_{\mathrm{D}}^{2}+R_{\mathrm{D}} \right) \end{aligned} Vn,out2=(Vn,out2+Vn,out2)RD2+2(4kTRD)=8kT(γgmRD2+RD)
V n , i n 2 ‾ = 8 k T ( γ g m + 1 g m 2 R D ) (如果用半边电路法看,全差分 V n , i n 2 ‾ 为半边电路值的 2 倍) \overline{V_{n,in}^{2}}=8kT\left( \frac{\gamma}{g_m}+\frac{1}{g_{\mathrm{m}}^{2}R_{\mathrm{D}}} \right) \\ \text{(如果用半边电路法看,全差分}\overline{V_{n,in}^{2}}\text{为半边电路值的}2\text{倍)} Vn,in2=8kT(gmγ+gm2RD1)(如果用半边电路法看,全差分Vn,in2为半边电路值的2倍)
7.7 功率与噪声的折中
在保持电压增益( A V = − g m R D ⟹ A V = − g m 2 ⋅ 2 R D A_V=-g_mR_D\Longrightarrow A_V=-\frac{g_m}{2}\cdot 2R_D AV=−gmRD⟹AV=−2gm⋅2RD)和输出摆幅不变( max = V D D − I D R D ⟹ max = V D D − 2 I D ⋅ R D 2 \max =\mathrm{V}_{\mathrm{DD}}-\mathrm{I}_{\mathrm{D}}\mathrm{R}_{\mathrm{D}}\Longrightarrow \max =\mathrm{V}_{\mathrm{DD}}-2\mathrm{I}_{\mathrm{D}}\cdot \frac{\mathrm{R}_{\mathrm{D}}}{2} max=VDD−IDRD⟹max=VDD−2ID⋅2RD)的前提下,输入参考热噪声( V n , i n 2 ‾ = 4 k T γ g m (g m 变大) \overline{V_{n,in}^{2}}=\frac{4kT\gamma}{g_m}\text{(g}_{\mathrm{m}}\text{变大)} Vn,in2=gm4kTγ(gm变大))和闪烁噪声的功率( V n , i n 2 ‾ = K C o x W L ⋅ 1 f (W变大) \overline{V_{n,in}^{2}}=\frac{K}{C_{ox}WL}\cdot \frac{1}{f}\text{(W变大)} Vn,in2=CoxWLK⋅f1(W变大))为原来的⼀半,功率的下降是由功耗加倍( I D 加倍 I_D 加倍 ID加倍)为代价换来的。
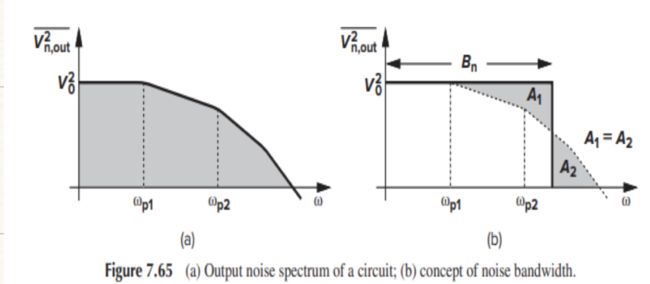
7.8 噪声带宽
总噪声功率 V n , o u t , t o t 2 ‾ = ∫ 0 ∞ V n , o u t 2 ‾ d f = V 0 2 ⋅ B n 带宽 B n = π f 3 d B 2 (单极点系统) \text{总噪声功率}\overline{V_{n, \mathrm{out} , \mathrm{tot}}^{2}}=\int_0^{\infty}{\overline{V_{n, \mathrm{out}}^{2}}}df=V_{0}^{2}\cdot B_n \\ \text{带宽}B_n=\frac{\pi f_{3dB}}{2}\text{(单极点系统)} 总噪声功率Vn,out,tot2=∫0∞Vn,out2df=V02⋅Bn带宽Bn=2πf3dB(单极点系统)
得到带宽越大,总噪声功率越大
7.9 输入噪声积分的问题
输出总噪声, 是 0 到无穷大频率的电压功率谱积分, 与传递函数形状有关。输入参考噪声 (非测量出的抽象数值), 没有传递函数概念, 不能对输入功率谱积分。
7.10 (补充)运放的噪声计算【原本是第九章的内容放到了这里⼀起讲】
7.10.1 折叠cascode
-
噪声的主要来源:输入管 M1 和负载电流源 M7
-
M3 和 M5 噪声在低频时影响较⼩,因为 Vb1、Vb2 上的噪声在输出端上的增益较小,对输出噪声电压的贡献较小;在高频时由于S级寄⽣电容容抗减小,噪声增加。【共源共栅级噪声部分讲过】
-
输入参考噪声电压功率
V n 2 ‾ = 4 k T ( 2 γ g m 1 , 2 + 2 γ g m 7 , 8 g m 1 , 2 2 ) + 2 K N ( W L ) 1 , 2 C o x f + 2 K P ( W L ) 7 , 8 C o x f g m 7 , 8 2 g m 1 , 2 2 \overline{V_{n}^{2}}=4kT\left( 2\frac{\gamma}{g_{m1,2}}+2\frac{\gamma g_{m7,8}}{g_{m1,2}^{2}} \right) +2\frac{K_N}{(WL)_{1,2}C_{ox}f}+2\frac{K_P}{(WL)_{7,8}C_{ox}f}\frac{g_{m7,8}^{2}}{g_{m1,2}^{2}} Vn2=4kT(2gm1,2γ+2gm1,22γgm7,8)+2(WL)1,2CoxfKN+2(WL)7,8CoxfKPgm1,22gm7,82
7.10.2 两级放大器
V n , t o t 2 ‾ = 8 k T γ 1 g m 1 2 [ g m 1 + g m 3 + g m 5 + g m 7 g m 5 2 ( r O 1 ∥ r O 3 ) 2 ] (噪声主要取决于第一级) \overline{V_{n,tot}^{2}}=8kT\gamma \frac{1}{g_{m1}^{2}}\left[ g_{m1}+g_{m3}+\frac{g_{m5}+g_{m7}}{g_{m5}^{2}\left( r_{O1}\parallel r_{O3} \right) ^2} \right] \text{(噪声主要取决于第一级)} Vn,tot2=8kTγgm121[gm1+gm3+gm52(rO1∥rO3)2gm5+gm7](噪声主要取决于第一级)