代码随想录Day15 二叉树进入层序遍历阶段
102.二叉树的层序遍历
题目
给你一个二叉树,请你返回其按 层序遍历 得到的节点值。 (即逐层地,从左到右访问所有节点)。
示例 1:
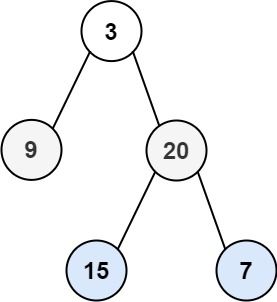
输入:root = [3,9,20,null,null,15,7] 输出:[[3],[9,20],[15,7]]
思考
非常重要!非常重要!非常重要!关键的话说三遍,层序遍历就是一层层遍历二叉树的值,图中一目了然可看到一个问题,怎么从左结点跳到右结点并且将左结点和右结点都取出来呢?这时候有一个关键的数据结构queue就登场了,queue的特点就是先进先出,正好可以拿来做我们这题,总结下来层序遍历分为以下几步:
1、判断root是否不为null并且创建queue,queue里的数据类型是TreeNode,将root先装进queue里
2、进入循环,条件是queue不为空,接下来是关键,设一个变量size等于queue的size,接着再接一个循环size--,这里size的目的是为了把二叉树每一层元素的个数都用size表示出来,即确定每一层要循环多少次
3、确定queue的存取方式,即每次size-1时都从queue取一个元素出来,然后将这个元素的左右孩子放进queue里,注意因为queue是先进先出,那么当size=0时正好把每一层的元素都取完,虽说当时queue里的元素不为空。
代码
class Solution {
public:
vector
queue
vector
if (root == NULL) return res;
// 用que来做层序,因为queue先进先出
que.push(root);
while (!que.empty()) {
// 每一层的size要记录,相当于每一层遍历的次数
int size =que.size();
vector
while(size--) {
TreeNode* node = que.front();//在弹出前先记录node,因为下面要把node的left和right都加进que
que.pop();
tmp.push_back(node->val);
if (node->left) que.push(node->left);
if (node->right) que.push(node->right);
}
res.push_back(tmp);
}
return res;
}
};
226.翻转二叉树
题目
给你一棵二叉树的根节点 root ,翻转这棵二叉树,并返回其根节点。
示例 1:
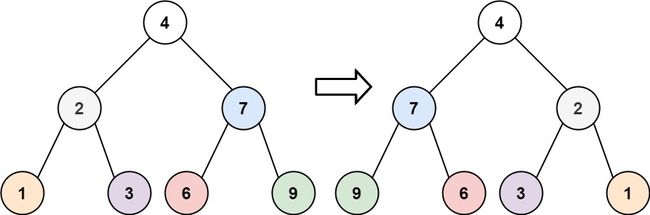
输入:root = [4,2,7,1,3,6,9] 输出:[4,7,2,9,6,3,1]
思考
没啥难度,就是遍历二叉树,但是要存左右接点时先把左右结点swap一下
代码
// BFS迭代
class Solution {
public:
TreeNode* invertTree(TreeNode* root) {
queue
if(root == nullptr) return root;
que.push(root);
while(!que.empty()) {
int size = que.size();
while(size--) {
TreeNode*node = que.front();
que.pop();
swap(node->left, node->right);
if(node->left) que.push(node->left);
if(node->right) que.push(node->right);
}
}
return root;
}
};
// DFS迭代
class Solution {
public:
TreeNode* invertTree(TreeNode* root) {
stack
if(root == NULL) return root;
stk.push(root);
while (!stk.empty()) {
TreeNode* node = stk.top();
stk.pop();
swap(node->left, node->right);
if(node->left) stk.push(node->left);
if(node->right) stk.push(node->right);
}
return root;
}
};
101. 对称二叉树
题目
给定一个二叉树,检查它是否是镜像对称的
示例 1:
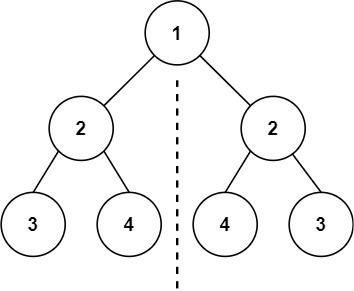
输入:root = [1,2,2,3,4,4,3] 输出:true
思考
感觉有点难度,一时间不知道用哪种遍历方法比较好,联想到上题做过的翻转二叉树,想着要不层序遍历一下,如果将二叉树翻转后与原二叉树相等,则证明这个二叉树是对称的,但如何证明两个相等呢,思考良久,感觉不太行,后又看卡哥视频,发现需要用后序遍历的方法,因为后序遍历是左右中,与本题方向相符,本题除了使用后序遍历的思想,关键主要有两点:
1、需要判断二叉树左外侧与右外侧结点、左内侧与右内侧结点是否相等,例如图中的左3与右3,左4与右4
2、需要将二叉树左外侧、右外侧、左内侧、右内侧结点依次放入queue中,在判断的时候取出头两个进行判断。
代码
class Solution {
public:
bool isSymmetric(TreeNode* root) {
if(root == nullptr) return false;
queue
que.push(root->left);
que.push(root->right);
// 采用后序遍历,后序遍历的条件是需要收集孩子的信息返回给根结点
while(!que.empty()) {
TreeNode* leftNode = que.front();//左
que.pop();
TreeNode* rightNode = que.front();//右
que.pop();
if(!leftNode && !rightNode) continue;//关键,因为左右结点均为空说明是对称的
if (!leftNode || !rightNode || leftNode->val != rightNode->val) return false;//中
que.push(leftNode->left);
que.push(rightNode->right);
que.push(leftNode->right);
que.push(rightNode->left);
}
return true;
}
};