【算法学习】简单多状态-动态规划

前言

        本篇博客记录动态规划中的简单多状态问题。

        在之前的动态规划类型的题中，我们每次分析的都只是一种或者某一类的状态，定义的dp表也是围绕着一种状态来的。

        现在可能对于一种状态，存在几种不同的子状态，在状态转移过程中相互影响。此时需要多个dp表相互进行状态转移。

目录

一、打家劫舍Ⅰ

题目解析：

编码：

二、打家劫舍Ⅱ

题目解析：

编码： 

三、删除并获得点数

题目解析：

编码： 

四、粉刷房子

题目解析：

编码： 

五、买卖股票的最佳时期Ⅳ

题目解析：

编码： 

---

一、打家劫舍Ⅰ

题目链接：力扣（LeetCode）官网 - 全球极客挚爱的技术成长平台

题目解析：

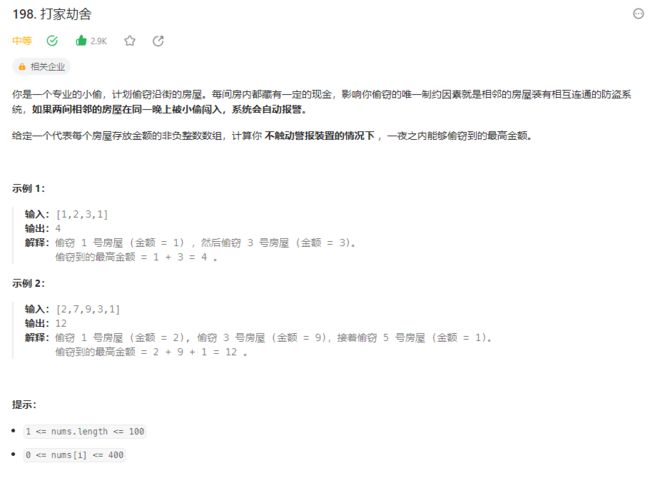
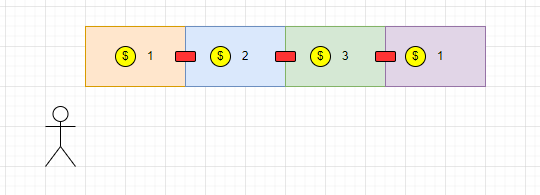
        根据题目，我们以实例一为例：

        不同颜色的表格表示不同的房子，内显示的$数就是对应的资金，红色表示相邻房子如果同时被盗窃会触发报警。

        现在小偷需要在不触发报警的条件下，一夜之内偷盗的最高金额（这一排房子）。

        我们可以将题目问的问题根据表格翻译以下：从这一排表格中，在不连续取两个相邻各自内数的条件下，能够取到的最高数值和。

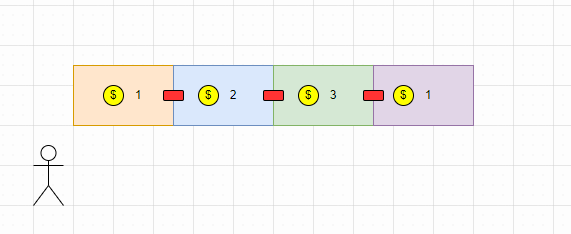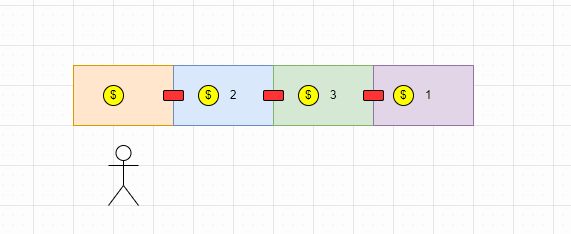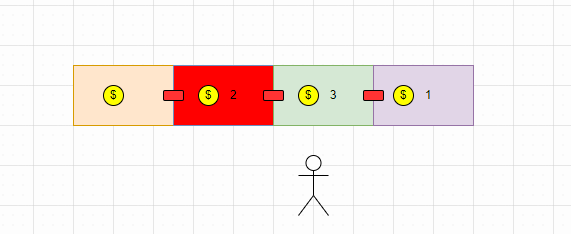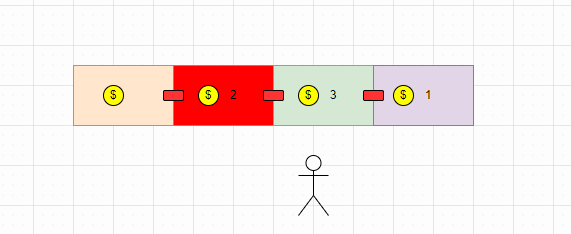
        对于上述示例，小偷可以先取1（0号位置），然后取3（2号位置），就能够获得最高金额了。

        对于动态规划题目，我们首先应该确定一个状态表示。根据题目，很简单的就可以确定：到达第i个房子后偷得得最高金额。 

        但是，根据题目的限制条件，影响着能否对该房子盗取的因素：相邻不能同时盗取。而这个取决于你是否对之前的房子进行了盗取。

对于到达第i个房子后偷得得最高金额状态存在两个子状态：

1.对当前房子偷取后得总共最高金额。f[i]

2.对当前房子不偷后得到得总最高金额。g[i] 

        这个两个状态相互制约，所以我们需要不同的dp表对其进行表示 ，可以采用上面的f和g。

        确定好状态表示后，我们就需要确认状态转移方程了。

此处的状态简单，可以直接进行分析。

对于f状态（偷窃此房子），就近分析，上一次（相邻的房子）可以偷窃吗？不行，偷窃的话就会被逮住，所以只能上一次没有偷窃，加上这次偷窃的金额即可。

对于g状态（不偷窃此房子），上一次可以偷窃也可以没有偷窃，那么要得到最高，需要求max。

        所以，我们的状态转移方程对于两个子状态均存在：

f[i] = g[i - 1] + nums[i];

g[i] = max(f[i - 1], g[i - 1]);

其中，nums[i]表示此次房子内的金额数。

        为了防止越界，我们可以对f[0]和g[0]初始化即可。

        f[0]表示对第一间房子偷：那么就是nums[0]即可；g[0]不偷就是0。

        填表顺序自然是从左到右，并且两个dp表同时初始化。返回值就是max(f[n - 1], g[n - 1])即可。

编码：

class Solution {
public:
    int rob(vector& nums) {
        int n = nums.size();
        // 创建dp表
        vector f(n);
        auto g = f;
        // 初始化
        f[0] = nums[0];
        // 填表
        for (int i = 1; i < n; ++i)
        {
            f[i] = g[i - 1] + nums[i];
            g[i] = max(g[i - 1], f[i - 1]);
        }
        return max(f[n - 1], g[n - 1]);
    }
};

时间复杂度：O(n);

空间复杂度：O(n); 

二、打家劫舍Ⅱ

题目链接：力扣（LeetCode）官网 - 全球极客挚爱的技术成长平台

题目解析：

        根据题意，我们以示例2为例子，可以得到下面这张图：

        可以发现，此时，小偷从一横排变成了一个环形的偷法。此时相邻的两间还是存在红色的报警器。

        那么现在，小偷该如何去偷使其钱最大呢？

        我们还是按照1的思路，设置一个总的状态表示：小偷偷盗i间房子为止，偷窃到的最高金额。

        还是和上题一样，此状态细分存在子状态。就是此时对此间房子偷还是不偷。但是和打家劫舍Ⅰ不同的是，如果你偷了第一间房子，那么最后一间房是不能偷的。

        我们可以对此不同的条件进行一个分析：也就是说，如果小偷偷了第一间房子，那么除开第一间、第二间房子和最后一间房子，其余都是Ⅰ的逻辑。同理，如果不偷，那么从第二间房子开始就都是Ⅰ的逻辑。

        很巧妙，我们可以分情况，将特殊的情况进行分开就可以进行正常的动态规划环节。

        剩下的分析和Ⅰ一致，只不过需要注意初始化和映射问题，详细可以看编码区别。

编码： 

class Solution {
public:
    // 子函数，用于求一个范围内的最高金额，相邻之间不可同时偷
    int _rob(vector& nums, int start, int end)
    {
        if (end < start) return 0;

        int n = end - start + 1;
        // 创建dp表
        vector f(n);
        auto g = f;

        // 初始化
        f[0] = nums[start];
        // 填表
        for (int i = 1; i < n; ++i)
        {
            f[i] = g[i - 1] + nums[start + i];
            g[i] = max(g[i - 1], f[i - 1]);
        }
        return max(g[n - 1], f[n - 1]);
    }
    int rob(vector& nums) {
        int n = nums.size();
        // 分情况，将环形拆分
        // 1 第一个房子偷
        int x = nums[0];
        x += _rob(nums, 2, n - 2);
        // 第一个房子不偷
        int y = 0;
        y += _rob(nums, 1, n - 1);
        return max(x, y);
    }
};

时间复杂度：O(n)

空间复杂度：O(n) 

三、删除并获得点数

题目链接：力扣（LeetCode）官网 - 全球极客挚爱的技术成长平台

题目解析：

        题目的意思就是可以选择一个位置的点数，获得它，但是需要删除nums[i] + 1和nums[i] - 1的所有值（不能获取）。

        从获取和不获取以及+1和-1，你看是不是和相邻间隔不能同时获取相像呢？现在有个问题，nums的数组似乎不是连续的。

        如果我们能够将nums的值转换为一个下标，对应数组的值就是对应下标在nums中的之和。这样是不是就可以转换为打家劫舍问题？

        下标不存在的对应值为0即可。我们以示例2为例，转换一下：

nums = [2, 2, 3, 3, 3, 4]

转换为对应数组num

num =[0, 0, 4, 9, 4]

        可以转换为打家劫舍问题，连续的并且间隔不能想偷：

        9

        根据题目条件，因为数组的最大值不超过10^4，所以我们可以设置数组大小为10001即可，第一次的时候按照对应值进行映射，随后转换为上面的解法即可。

        详情请看编码。

编码： 

class Solution {
public:
    int deleteAndEarn(vector& nums) {
        int n = nums.size();
        const int N = 10001;
        // 预处理，转换为打家劫舍1
        int nums2[N] = {0};
        for(auto x : nums) nums2[x] += x;

        // 动归问题现在开始！
        // 创建dp表
        vector f(N);
        auto g = f;
        // 填表
        for (int i = 1; i < N; ++i)
        {
            f[i] = g[i - 1] + nums2[i];
            g[i] = max(f[i - 1], g[i - 1]);
        }
        return max(f[N - 1], g[N - 1]);
    }
};

时间复杂度：O(10^4)

空间复杂度：O(10^4) 

四、粉刷房子

题目链接：力扣（LeetCode）官网 - 全球极客挚爱的技术成长平台

题目解析：

        实际上也是相邻问题的变种，此时主状态是：到第i间房子的花费最小成本。

        子状态分别是：到第i间房子刷红色的最小成本、到第i间房子刷蓝色的最小成本、到第i间房子刷绿色的最小成本。

        而相邻之间不能同时的限制条件则变成了颜色不能相同，那么状态转移也就变成了另外两种颜色上次粉刷的最小成本罢了。

        因为存在三种状态，我们可以设置dp表为一个n*3的2维数组。那么状态转移方程为：

dp[i][0] = costs[i][0] + min(dp[i - 1][1], dp[i - 1][2]); 红色

dp[i][1] = costs[i][1] + min(dp[i - 1][0], dp[i - 1][2]); 蓝色

dp[i][2] = costs[i][2] + min(dp[i - 1][1], dp[i - 1][0]); 绿色

        需要初始化dp[0][]罢了，后面的0、1、2分别对应costs[0][0]、costs[0][1]、costs[0][2]即可。

编码： 

class Solution {
public:
    int minCost(vector>& costs) {
        int n = costs.size();
        // 创建dp表
        vector> dp(n, vector(3));  // 红色 0 蓝色1 绿色2
        // 初始化
        dp[0][0] = costs[0][0];
        dp[0][1] = costs[0][1];
        dp[0][2] = costs[0][2];
        // 填表
        for (int i = 1; i < n; ++i)
        {
            dp[i][0] = costs[i][0] + min(dp[i - 1][1], dp[i - 1][2]);
            dp[i][1] = costs[i][1] + min(dp[i - 1][0], dp[i - 1][2]);
            dp[i][2] = costs[i][2] + min(dp[i - 1][1], dp[i - 1][0]);
        }
        return min(dp[n - 1][0], min(dp[n - 1][1], dp[n - 1][2]));
    }
};

五、买卖股票的最佳时期Ⅳ

题目链接：力扣（LeetCode）官网 - 全球极客挚爱的技术成长平台

题目解析：

        此题是买卖股票的最佳时机的变种。

        因为题目中的信息（必须在再次购买之前出售掉之前的股票），在之前的买卖股票题目中（除开了k笔交易，意思是可以无限交易），存在两种子状态：1.拥有股票，2.没有股票。针对这两种子状态进行分析即可。

        但是此题限制了条件：最多可以完成k次交易。

        那么状态就可以细化为第i次交易拥有股票状态和第i次交易没有股票状态（0<=i<=k）。

        所以对应的，我们给原本的两个子状态更上k次交易这个维度即可。并且注意到，卖掉的那一刻可以算作一次交易。（和后面的状态转移方程式密切相关）

        所以状态可以表示为：

f[i][j]:以i结尾，拥有股票此时第j笔交易的最大利润。

g[i][j]:以i结尾，没有股票此时第j笔交易的最大利润。

        有了状态，我们可以就近原则去想状态转移方程。

        之前的股票交易题我们是考虑到当天如果有股票，那么前一天要么没股票，今天买，要么前一天有股票，今天不买。当天如果没有股票，要么前一天没股票，今天也不买，要么前一天有股票，今天卖了。

        而这次，只是加上了一个交易次数维度：当天有股票，是第j次交易，那么前一天要么没股票，今天买了。要么前一天有股票，今天没动；当天没股票，是第j次交易，要么前一天没有股票，今天没买，要么前一天有股票，第j-1次交易，今天卖了（因为今天卖了的缘故，所以交易数得增加）。

        分析到状态可以很简单的得到下面的状态转移方程：

f[i][j] = max(f[i-1][j], g[i-1] - prices[i]);

g[i][j] = max(g[i-1][j], f[i-1][j-1] + prices[i]);

        得到状态转移方程后我们需要对其进行初始化。因为存在i-1和j-1.所以需要对第一行和第一列进行初始化。

        对于第一行，第一天不可能存在交易次数。因为存在交易次数的话，说明买了又卖了，没有任何意义。所以第一行对于拥有股票来说第一个元素（0次交易）初始化为对应股票的负数即可，其余设置为最小值不可影响其他状态（对于最小值，一般编程中习惯设置为-0x3f3f3f3f，最大值反过来即可）。没有股票表示啥也没干，第一个元素初始化为0即可。

        对于第一列，表示此时是第0笔交易，是没有之前的交易的，那么我们细看状态转移方程的话，只有没有股票状态表示的时候用到，可以利用在填表过程中设置条件来跳过初始化（j>0）即可，这也是一个很好的技巧。

        返回值的时候实在所有交易次数中判断最小即可（一般最后一次卖出股票肯定是比拥有股票最大利润最优的，所以只需要在卖出股票的几种交易情况中进行对比即可）

        另外，因为交易次数是题目中给的，我们存在对交易次数的优化方案：因为交易一次是值买一次卖一次。在最大利润的情况下是一天买，一天卖。所以交易次数最大不能超过总天数的一半。

编码： 

class Solution {
public:
    const int MIN = -0x3f3f3f3f;
    int maxProfit(int k, vector& prices) {
        int n = prices.size();
        // 处理细节问题
        k = min(k, n / 2);
        // 创建dp表
        vector> f(n, vector(k + 1, MIN));
        auto g = f;
        // 初始化
        f[0][0] = -prices[0];
        g[0][0] = 0;
        // 填表
        for (int i = 1; i < n; ++i)
        {
            for (int j = 0; j <= k; ++j)
            {
                f[i][j] = max(f[i - 1][j], g[i - 1][j] - prices[i]);
                g[i][j] = g[i - 1][j];
                if (j > 0) g[i][j] = max(g[i - 1][j], f[i - 1][j - 1] + prices[i]);
            }
        }
        // 返回值
        int res = g[n - 1][0];
        for (int i = 1; i <= k; ++i) res = max(res,g[n - 1][i]);
        return res; 
    }
};

时间复杂度：O(n*k)

空间复杂度：O(n*k)