代码随想录刷题笔记(DAY 7)
今日总结:前端开始学习 vue3 的新特性,花费时间比较多,今天的题目后面有点难度,明天抽时间复习一下。
Day 7
01. 四数相加 II(No. 454)
题目链接
代码随想录题解
1.1 题目
给你四个整数数组 nums1、nums2、nums3 和 nums4 ,数组长度都是 n ,请你计算有多少个元组 (i, j, k, l) 能满足:
0 <= i, j, k, l < nnums1[i] + nums2[j] + nums3[k] + nums4[l] == 0
示例 1:
输入:nums1 = [1,2], nums2 = [-2,-1], nums3 = [-1,2], nums4 = [0,2]
输出:2
解释:
两个元组如下:
- (0, 0, 0, 1) -> nums1[0] + nums2[0] + nums3[0] + nums4[1] = 1 + (-2) + (-1) + 2 = 0
- (1, 1, 0, 0) -> nums1[1] + nums2[1] + nums3[0] + nums4[0] = 2 + (-1) + (-1) + 0 = 0
示例 2:
输入:nums1 = [0], nums2 = [0], nums3 = [0], nums4 = [0]
输出:1
1.2 笔记
和前面说的一样,我们在考虑一个题能不能用哈希法解决的时候首先要想:
我们需不需要知道某一个数字在之前有没有出现过。
求和,很容易想到 target - 现在遍历到的数字 是否在之前遍历的数字中出现过
我们先将 nums1 和 nums2 中的数据求和放到 map 中,然后当我们去便利 nums3 和 nums4 的时候就可以检查需要的数据是否出现过
出现了之后应该使得 resNum 加上多少呢?
很多人可能想当然的是 1(比如我),但是因为这道题不需要去重,我们需要知道是多少 种 组合,所以加的是这个值出现的次数。
1.3 代码
class Solution {
public int fourSumCount(int[] nums1, int[] nums2, int[] nums3, int[] nums4) {
Map<Integer, Integer> oneAddTwo = new HashMap<>();
List<Integer> threeAddFour = new ArrayList<>();
int length = nums1.length;
int resNum = 0;
// 存储 nums1 和 nums2 的和
for (int i = 0; i < length; i++) {
for (int j = 0; j < length; j++) {
int sum1 = nums1[i] + nums2[j];//求前两个数组的和
if (oneAddTwo.containsKey(sum1)) {
oneAddTwo.put(sum1, oneAddTwo.get(sum1) + 1);
} else {
oneAddTwo.put(sum1, 1);
}
}
}
for (int i : nums3) {
for (int j : nums4) {
if (oneAddTwo.containsKey(0 - i - j)) {
resNum += oneAddTwo.get(0 - i - j);
}
}
}
return resNum;
}
}
02. 赎金信(No. 383)
题目链接
代码随想录题解
2.1 题目
给你两个字符串:ransomNote 和 magazine ,判断 ransomNote 能不能由 magazine 里面的字符构成。
如果可以,返回 true ;否则返回 false 。
magazine 中的每个字符只能在 ransomNote 中使用一次。
示例 1:
输入:ransomNote = “a”, magazine = “b”
输出:false
示例 2:
输入:ransomNote = “aa”, magazine = “ab”
输出:false
示例 3:
输入:ransomNote = “aa”, magazine = “aab”
输出:true
提示:
1 <= ransomNote.length, magazine.length <= 105ransomNote和magazine由小写英文字母组成
2.2 笔记
非常经典的哈希法可以解决的题目,检测 ransomNote 中的数字是否在 magazine 中出现过且数量足够(每个字母只能用一次)
这道题目比较简单,直接上代码了
2.3 代码
class Solution {
public boolean canConstruct(String ransomNote, String magazine) {
// 转化为字符串数组
char[] m = magazine.toCharArray();
char[] r = ransomNote.toCharArray();
int[] hash = new int[26];
for(int i = 0; i < m.length; i++) {
hash[m[i] - 'a']++;
}
for (int i = 0; i < r.length; i++) {
// 检测是否出现负数
if (--hash[r[i] - 'a'] < 0) {
// 出现负数直接返回 false
return false;
}
}
return true;
}
}
03. 三数之和
题目链接
代码随想录题解
3.1 题目
给你一个整数数组 nums ,判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i != j、i != k 且 j != k ,同时还满足 nums[i] + nums[j] + nums[k] == 0 。请
你返回所有和为 0 且不重复的三元组。
**注意:**答案中不可以包含重复的三元组。
示例 1:
输入:nums = [-1,0,1,2,-1,-4]
输出:[[-1,-1,2],[-1,0,1]]
解释:
nums[0] + nums[1] + nums[2] = (-1) + 0 + 1 = 0 。
nums[1] + nums[2] + nums[4] = 0 + 1 + (-1) = 0 。
nums[0] + nums[3] + nums[4] = (-1) + 2 + (-1) = 0 。
不同的三元组是 [-1,0,1] 和 [-1,-1,2] 。
注意,输出的顺序和三元组的顺序并不重要。
示例 2:
输入:nums = [0,1,1]
输出:[]
解释:唯一可能的三元组和不为 0 。
示例 3:
输入:nums = [0,0,0]
输出:[[0,0,0]]
解释:唯一可能的三元组和为 0 。
提示:
3 <= nums.length <= 3000-105 <= nums[i] <= 105
3.2 笔记
因为前面一直在做哈希表的题目,我下意识的想用哈希表法来解这道题目(也算是分模块刷题的一种弊端吧)
但是我们会发现,这道题目要去重的点太多了,三个位置都需要去重,哈希法解题限制条件非常多。
这里给出一种思路,利用双指针的方法去做。
我们先将数组排好序,这也是为了 去重 做准备的,排序之后相同大小的数据会排列在一起。
具体的思路是这样的:我们定义一个左指针和一个右指针,循环遍历整个数组,循环变量为 i ,左指针指向 i+1,右指针指向数组的最后一个元素,我们来确定这三个变量的和是否大于我们的 target 也就是 0
-
如果是大于零的情况,说明我们的和需要缩小,也就是右指针要向前移动
-
如果是小于零的情况,说明我们的和需要变大,也就是左指针要向前移动
-
当我们结果等于零的时候,就直接保存下来 吗?
当然不是,我们要针对做指针和右指针进行去重,这个去重的目的是为了避免同一种情况的多次出现
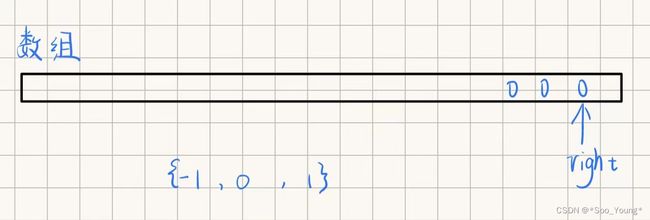
比如上面的这种情况,如果我们不进行去重的话,会得到三个 [-1, 0, 1]
对于 i 的去重也是相同的原理,但是我们要考虑``left` 的情况
比如我们的数组是 [-1, -1, -1 …………] 的话,我们遍历到第二个 -1 的时候其实在第一个 -1 已经包含了全部的情况,比如说 nums[left = i] 的情况,所以当我们发现正在遍历的 nums[i] 和 nums[i - 1] 相同的时候就可以直接跳过了。
现在三个数字的去重都已经考虑好了,参考一下我的代码
3.3 代码
class Solution {
List<List<Integer>> resList = new ArrayList<>();
public List<List<Integer>> threeSum(int[] nums) {
Arrays.sort(nums); // 排序
for (int i = 0; i < nums.length; i++) {
if (nums[i] > 0) {
return resList;
}
if (i > 0 && nums[i] == nums[i - 1]) {
continue;
}
int left = i + 1;
int right = nums.length - 1;
while (right > left) {
int sum = nums[i] + nums[left] + nums[right];
if (sum > 0) {
right--;
} else if (sum < 0) {
left++;
} else {
resList.add(Arrays.asList(nums[i], nums[left], nums[right]));
// 去重逻辑应该放在找到一个三元组之后,对b 和 c去重
while (right > left && nums[right] == nums[right - 1]) {
right--;
}
while (right > left && nums[left] == nums[left + 1]) {
left++;
}
right--;
left++;
}
}
}
return resList;
}
}