力扣题解22-25

22 括号生成

中等题

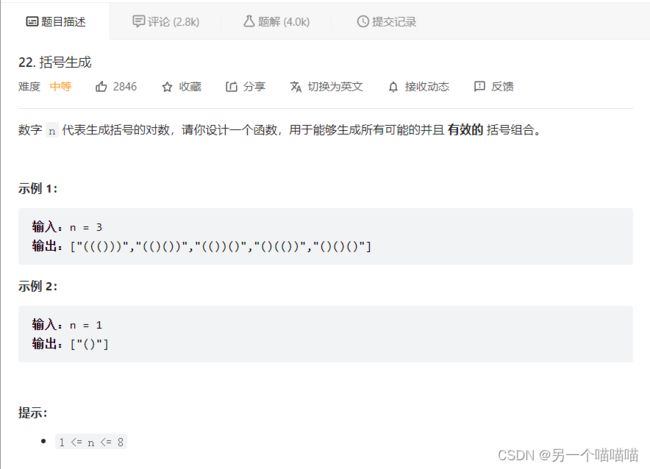
题目要求找到所有的组合，即是一道搜索所有可能的题。因为是要找到所有的解，一般想到回溯法。

回溯法

回溯法，就是按照某种选优条件往前搜索，在当前解的基础上一步步扩大解的范围。当某次扩大后发现该解不存在，则放弃该解，向后回退一步，继续探索其余可能的解。特点就是并不是一次搜索失败就从头开始重新搜索。
从图形的角度理解，回溯法搜索对应的是一棵多叉树，这棵多叉树的所有节点即是回溯法的回溯过程中会经过的所有可能性，当然我们最终追求的结果可能是全部节点，或者仅仅是叶子节点。回溯法所做的就是按照深度遍历的顺序到达每个叶子节点。
回溯法的一般流程如下：

0. 如果有必要，对需要遍历的序列（一维数组，二维数组…）进行排序。
1. 创建递归函数。函数的参数至少有：用于记录有效结果的result，用于记录当前路径的path（可能是各种类型，字符串，数组等），当前位置坐标（能表示当前处于多叉树的哪个位置）。
2. 在递归内部决定有效结果的条件，有效则将path存储入result。
3. 在递归进入下一层的后面记得写回溯。

下面就以本例题为例，展示回溯法的应用。

开始前还是再分析一下为什么要用回溯，搞清楚什么时候用什么算法还是很重要的。每个符合题意的结果都应该是一个长度为2n的、由n个’('和n个‘)’组成的字符串（当然还要满足“有效”这个条件）。而如何产生这个结果，需要从空字符串开始，每次向其中添加一个字符（这么说只是打个比方，可能有人会想一对一对字符加，总之就是逐渐添加）。这就是深度搜索的过程。如果只要找到一组可能的解，那就是搜索题。但是如果要找到所有可能的解，必须遍历所有可能的结果，这就是回溯。

本例的递归函数需要参数res来保存有效的结果，一个字符串cur表示当前的递归path，left表示左括号个数，right表示右括号个数，这两个能正确反映当前位置，n是递归停止条件。

#include 
#include 

using namespace std;

class Solution {
public:
    vector<string> generateParenthesis(int n) {
        vector<string> res;
        string cur;
        backtract(res,cur,0,0,n);
        return res;
    }

    //回溯法函数的特点：一个递归函数。当某次递归到了尽头，会回到上次的地方往下继续执行。递归到尽头一般会 1、表示这次结果满足条件，存储下来； 2、做判断，判断是否成立。
    //所以这种递归函数一般无返回值，因为结果另外存储了。当然，递归函数要体现递推关系，这就需要具体问题具体分析。
    void backtract(vector<string>& res, string& cur, int left, int right, int n){
        //注意字符向量和字符串是引用，是用于递归中存储数据的
        if(cur.size() == n*2){
            //长度足够
            res.push_back(cur);
            return ;
        }
        if(left<n){
            //左括号个数小于n，应该在字符串后面放置一个左括号
            cur.push_back('(');
            backtract(res,cur,left+1,right,n);
            cur.pop_back();  //回溯法就是要回溯，当上面的递归走到头了还需要继续往下递归
        }
        if(right<left){
            //右括号比左括号少，应该在字符串后面放一个右括号
            cur.push_back(')');
            backtract(res,cur,left,right+1,n);
            cur.pop_back();
        }
    }
};

int main(){
    Solution st;
    int n = 3;
    vector<string> res;

    res = st.generateParenthesis(n);
    return 0;
}

我们可以设想，本题的回溯函数塑造了一棵二叉树。本题的遍历采用逐一在后添加字符的方式，必须左括号个数大于等于右括号个数，小于n。确定了这种遍历的方式，则cur就可以确定此时的路径。

23 合并K个升序链表

困难题

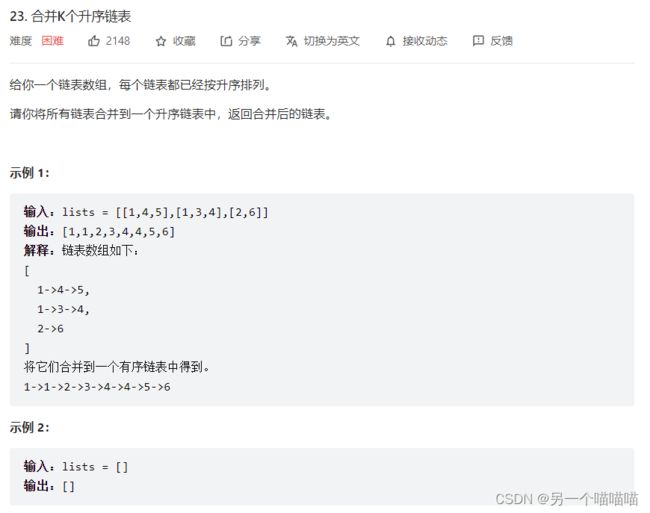
之前我们做过合并两个有序链表，用的是递归或者迭代的方法。将两个链表扩充成K个，我们很容易想到的一种一定可以的方法，就是迭代地两两合并链表，将其结果与下一个链表合并。这样就需要把“合并两个链表”这个操作重复k-1次，显然还有更好的方法。

分治法

分治法应用于能将大问题拆分成若干个解法相同的小问题的场合，即先分再治。这样，分成的子问题的解题过程和原来的问题相同，把得到的解合并起来正好就是原来问题的解。分治法通常依赖递归函数，函数有用于划分问题区间的参数。

struct ListNode {
    int val;
    ListNode *next;
    ListNode() : val(0), next(nullptr) {}
    ListNode(int x) : val(x), next(nullptr) {}
    ListNode(int x, ListNode *next) : val(x), next(next) {}
};

class Solution {
public:
    ListNode* mergeKLists(vector<ListNode*>& lists) {
        return merge(lists,0,lists.size()-1);
    }

    //合并两个链表
    ListNode* mergeTwoLists(ListNode* l1, ListNode* l2){
        ListNode* res;
        ListNode* cur;  
        if(!l1) return l2;
        if(!l2) return l1;
        if(l1->val < l2->val){
            res = l1;
            cur = l1;
            l1 = l1->next;
        }
        else{
            res = l2;
            cur = l2;
            l2 = l2->next;
        }
        while(l1 && l2){
            if(l1->val < l2->val){
                cur->next = l1;
                cur = l1;
                l1 = l1->next;
            }
            else{
                cur->next = l2;
                cur = l2;
                l2 = l2->next;
            }
        }
        if(!l1) cur->next = l2;
        else cur->next = l1;
        return res;
    }



    //参数应该是节点指针向量，两个表示起始位置和结束位置链表的下标，返回值应该是一个节点指针，并且已经排好序
    ListNode* merge(vector<ListNode*>& lists, int begin, int end){
        if(begin-end == 0) return lists[begin]; //该分组只有一个，不需要归并了
        if(begin>end) return nullptr; //返回一个空指针，反正连到那里都行
        int mid = (begin+end)/2;
        //分别计算左右两边后再合并
        return mergeTwoLists(merge(lists,begin,mid),merge(lists,mid+1,end));
    }
};

分治法还是要注意当把问题分到最小的时候改如何处理。例如本题中，采用二分，分到最后会出现1、合并一个链表（即左 = 一个链表，右 = 一个空链表），此时可以直接返回，因为空链表不需要合并 2、合并一个空链表（即左 = 右 = 空链表），那直接返回空指针。

24 两两交换链表中的节点

中等题

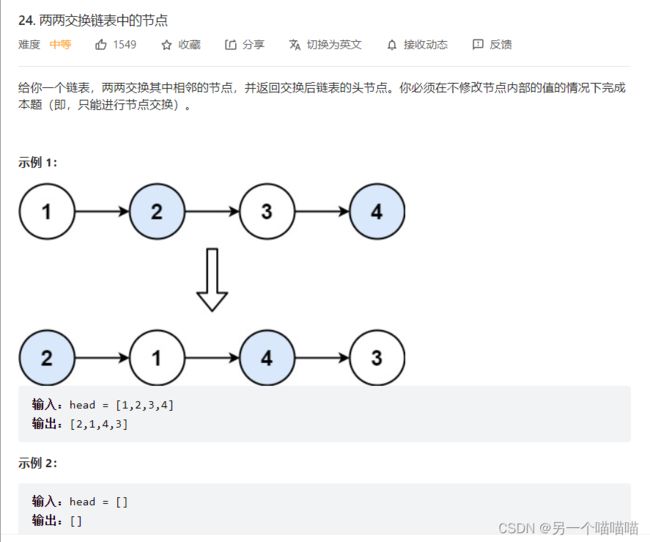
这个算简单题吧，太明显了，交换前两个+后面的递归，问题就解决了。

class Solution {
public:
    ListNode* swapPairs(ListNode* head) {
        if(!head || !head->next) return head;
        ListNode* nxt = head->next;
        head->next = swapPairs(nxt->next);
        nxt->next = head;
        return nxt;
    }
};

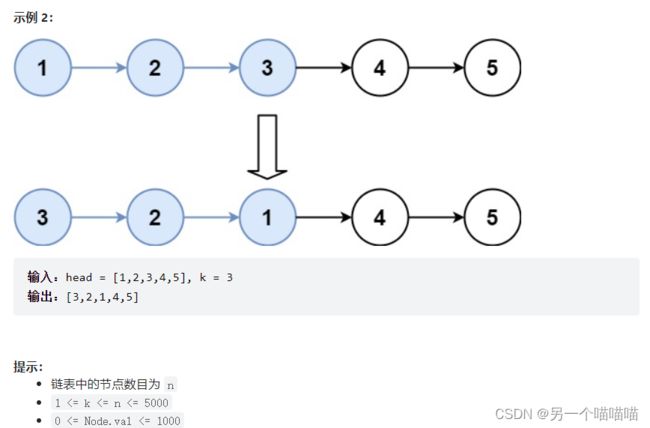
25 K个一组翻转链表

困难题

这一题是上一题的延伸。首先，当链表长度是2的时候，翻转链表仅仅是交换前后两个节点的位置，可以在常数时间内做到。当链表长度为K（K>2）的时候，翻转链表需要复杂一些的操作。在考虑多组长度为K的链表翻转之前，先必须以一组链表的翻转为基础。

让我们想象如何翻转一个链表：1→2→3→4。步骤应该是1←2→3→4，1←2←3→4，1←2←3←4，即每次将当前节点连接到前一个。注意一个细节，对于第一个节点，需要分配其下一个节点为nullptr。显然，这个翻转链表的形式有递推的特征：翻转第k个节点，就是在翻转好前k-1个节点的基础上，将第k个节点连接到k-1上。当然这个函数没必要写递归，简单的循环就可以完成了，只要每次记录当前节点和前一个节点。

 pair<ListNode*, ListNode*> reversek(ListNode* head, ListNode* tail){
        //已知头尾节点翻转链表，记录前一个和当前个
        ListNode* prv = tail->next; //反正随便指向一个空就行了
        ListNode* cur = head;
        while(prv != tail){
            ListNode* nxt = cur->next;
            cur->next = prv;
            prv = cur;
            cur = nxt;
        }
        return {tail,head};
    }

我觉得不带第二个参数tail也没问题，反正以nullptr为链表的结束就完了。不过这题有个“不满k个就不翻转”的条件，也就是总归要判断链表长度是否小于k的，那必须从头到尾跑一遍，也就肯定能拿到尾指针的值。
下面来讨论如何连接链表。第一，肯定要判断是否满k个。第二，如果满k个，翻转链表需要提供的参数是本次翻转的链表的头指针、尾指针。而连接需要的参数是上一个翻转后的尾指针、下一次翻转的头指针。因为连接链表要做的就是上一个翻转后的尾指针连接本次翻转后的头指针，本次翻转后的尾指针连接下一次翻转（当然也可能不足k个不翻转）后的头指针。理清逻辑后，代码其实并不难写。

class Solution {
public:
    ListNode* reverseKGroup(ListNode* head, int k) {
        //每k个翻转链表
        //先确定是否满k个
        ListNode* hair = new ListNode(0);
        hair->next = head;
        ListNode* pre = hair; //上一个分组的末尾

        while(head){
             ListNode* tail = pre; //当前分组的末尾
            // 查看剩余部分长度是否大于等于 k
            for (int i = 0; i < k; ++i) {
                tail = tail->next;
                if (!tail) {
                    return hair->next;
                }
            }
            ListNode* nex = tail->next; //这里必须保存，因为reverse会断掉这个连接，那么后一个节点就找不到了
            pair<ListNode*, ListNode*> result = reversek(head, tail);
            head = result.first;
            tail = result.second;
            //连接
            pre->next = head;
            tail->next = nex;
            //更新
            pre = tail;
            head = tail->next; //这里没问题，因为已经接好了
        }
        return hair->next;
    }

    pair<ListNode*, ListNode*> reversek(ListNode* head, ListNode* tail){
        //已知头尾节点翻转链表，记录前一个和当前个
        ListNode* prv = tail->next; //反正随便指向一个空就行了
        ListNode* cur = head;
        while(prv != tail){
            ListNode* nxt = cur->next;
            cur->next = prv;
            prv = cur;
            cur = nxt;
        }
        return {tail,head};
    }
};