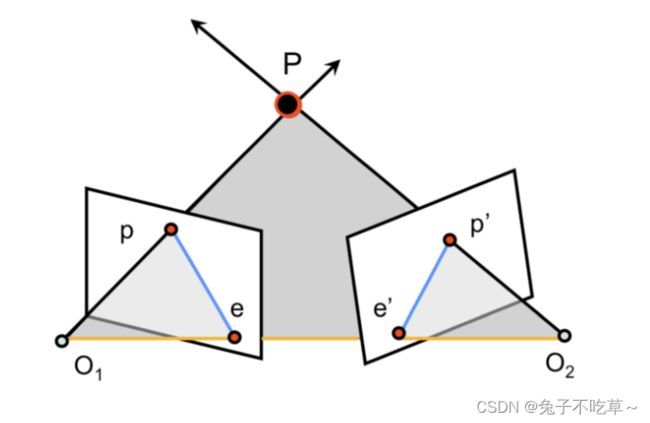
单目特征点对三角化

ORB-SLAM2之特征点对三角化

5 特征点对三角化

5.1 数学推导

  记P1,P2分别是第1、2帧对应的投影矩阵，它们将同一个空间点$X(X,Y,Z)$投影到图像上，对应特征匹配对$x_1、x_2$,$\lambda$表示系数，则上述过程可以表示如下：

$$\begin{array}{c}{\mathbf{x}}_1=\lambda {\mathbf{P}}_1\mathbf{X}\\ {\mathbf{x}}_2=\lambda {\mathbf{P}}_2\mathbf{X}\end{array}$$

  用矩阵来描述上面的公式（类似于直接线性变换DLT）
[ x y 1 ] = λ [ p 1 p 2 p 3 p 4 p 5 p 6 p 7 p 8 p 9 p 10 p 11 p 12 ] [ X Y Z 1 ] \begin{bmatrix}x\\y\\1\end{bmatrix}=\lambda\begin{bmatrix}p_1&p_2&p_3&p_4\\p_5&p_6&p_7&p_8\\p_9&p_{10}&p_{11}&p_{12}\end{bmatrix}\begin{bmatrix}X\\Y\\Z\\1\end{bmatrix} ​xy1​ ​=λ ​p1​p5​p9​​p2​p6​p10​​p3​p7​p11​​p4​p8​p12​​ ​ ​XYZ1​ ​

  简计为：
[ x y 1 ] = λ [ − P 0 − − P 1 − − P 2 − ] [ X Y Z 1 ] \begin{bmatrix}x\\y\\1\end{bmatrix}=\lambda\begin{bmatrix}-&P_0&-\\-&P_1&-\\-&P_2&-\end{bmatrix}\begin{bmatrix}X\\Y\\Z\\1\end{bmatrix} ​xy1​ ​=λ ​−−−​P0​P1​P2​​−−−​ ​ ​XYZ1​ ​

  等式两边叉乘坐标
[ x y 1 ] × [ x y 1 ] = [ x y 1 ] × λ [ − P 0 − − P 1 − − P 2 − ] [ X Y Z 1 ] \begin{bmatrix}x\\y\\1\end{bmatrix}\times\begin{bmatrix}x\\y\\1\end{bmatrix}=\begin{bmatrix}x\\y\\1\end{bmatrix}\times\lambda\begin{bmatrix}-&P_0&-\\-&P_1&-\\-&P_2&-\end{bmatrix}\begin{bmatrix}X\\Y\\Z\\1\end{bmatrix} ​xy1​ ​× ​xy1​ ​= ​xy1​ ​×λ ​−−−​P0​P1​P2​​−−−​ ​ ​XYZ1​ ​

  推导结果如下

[ x y 1 ] × [ − P 0 − − P 1 − − P 2 − ] [ X Y Z 1 ] = [ 0 0 0 ] \begin{bmatrix}x\\y\\1\end{bmatrix}\times\begin{bmatrix}-&P_0&-\\-&P_1&-\\-&P_2&-\end{bmatrix}\begin{bmatrix}X\\Y\\Z\\1\end{bmatrix}=\begin{bmatrix}0\\0\\0\end{bmatrix} ​xy1​ ​× ​−−−​P0​P1​P2​​−−−​ ​ ​XYZ1​ ​= ​000​ ​

  把叉积写为反对称矩阵
[ 0 − 1 y 1 0 − x − y x 0 ] [ − P 0 − − P 1 − − P 2 − ] [ X Y Z 1 ] = [ 0 0 0 ] \begin{bmatrix}0&-1&y\\1&0&-x\\-y&x&0\end{bmatrix}\begin{bmatrix}-&P_0&-\\-&P_1&-\\-&P_2&-\end{bmatrix}\begin{bmatrix}X\\Y\\Z\\1\end{bmatrix}=\begin{bmatrix}0\\0\\0\end{bmatrix} ​01−y​−10x​y−x0​ ​ ​−−−​P0​P1​P2​​−−−​ ​ ​XYZ1​ ​= ​000​ ​

  将前面两个矩阵乘出来，得到下面结果，注意下面第一个矩阵的第三行与前面两行线性相关，所以只保留线性无关的两行。也就是说，一个特征点可以提供两个约束等式
[ y P 2 − P 1 P 0 − x P 2 x P 1 − y P 0 ] [ X Y Z 1 ] = [ 0 0 0 ] \begin{bmatrix}yP_2-P_1\\P_0-xP_2\\xP_1-yP_0\end{bmatrix}\begin{bmatrix}X\\Y\\Z\\1\end{bmatrix}=\begin{bmatrix}0\\0\\0\end{bmatrix} ​yP2​−P1​P0​−xP2​xP1​−yP0​​ ​ ​XYZ1​ ​= ​000​ ​

  我们用$p$表示待求的三维点，$P_j^i$表示第$i$个投影矩阵的第$j$行，那么一对匹配点可以提供4个约束方程
[ y 1 P 2 1 − P 1 1 P 0 1 − x 1 P 2 1 y 2 P 2 2 − P 1 2 P 0 2 − x 2 P 2 2 ] p = [ 0 0 0 ] \begin{bmatrix}y_1P_2^1-P_1^1\\P_0^1-x_1P_2^1\\y_2P_2^2-P_1^2\\P_0^2-x_2P_2^2\end{bmatrix}\boldsymbol{p}=\begin{bmatrix}0\\\\0\\\\0\end{bmatrix} ​y1​P21​−P11​P01​−x1​P21​y2​P22​−P12​P02​−x2​P22​​ ​p= ​000​ ​

$$\begin{array}{c}Ap=0\\ \\ \end{array}$$

  和前面的求解一样，利用SVD求解，右奇异矩阵的最后一列就是最终的解，即三角化得到的三维点坐标。

5.2 代码分析

5.2.1 三角化

/** 给定投影矩阵P1,P2和图像上的匹配特征点点kp1,kp2，从而计算三维点坐标
 * @brief 
 * 
 * @param[in] kp1               特征点, in reference frame
 * @param[in] kp2               特征点, in current frame
 * @param[in] P1                投影矩阵P1
 * @param[in] P2                投影矩阵P2
 * @param[in & out] x3D         计算的三维点
 */
void Initializer::Triangulate(
    const cv::KeyPoint &kp1,    //特征点, in reference frame
    const cv::KeyPoint &kp2,    //特征点, in current frame
    const cv::Mat &P1,          //投影矩阵P1
    const cv::Mat &P2,          //投影矩阵P2
    cv::Mat &x3D)               //三维点
{
    cv::Mat A(4,4,CV_32F);

    //构造参数矩阵A
    A.row(0) = kp1.pt.x*P1.row(2)-P1.row(0);
    A.row(1) = kp1.pt.y*P1.row(2)-P1.row(1);
    A.row(2) = kp2.pt.x*P2.row(2)-P2.row(0);
    A.row(3) = kp2.pt.y*P2.row(2)-P2.row(1);

    //奇异值分解的结果
    cv::Mat u,w,vt;
    //对系数矩阵A进行奇异值分解
    cv::SVD::compute(A,w,u,vt,cv::SVD::MODIFY_A| cv::SVD::FULL_UV);
    //根据前面的结论，奇异值分解右矩阵的最后一行其实就是解，原理类似于前面的求最小二乘解，四个未知数四个方程正好正定
    // 用列向量来表示一个点的空间坐标
    x3D = vt.row(3).t();
    // 为了符合其次坐标的形式，使最后一维为1----归一化
    x3D = x3D.rowRange(0,3)/x3D.at<float>(3);
}

5.2.2 何处调用

  三角化的条件：已知匹配点对，投影矩阵，求解三维点。本质就是一个三维点在两幅图像上对应的像素点提供了4个方程约束。

  一般来讲，第一帧会被选择作为世界系，所以P1本质就是内参矩阵K。P2实际上就是第一帧到第二帧的变换矩阵$K{T}_{2w}$。

int Initializer::CheckRT(const cv::Mat &R, const cv::Mat &t, const vector<cv::KeyPoint> &vKeys1, const vector<cv::KeyPoint> &vKeys2,
                       const vector<Match> &vMatches12, vector<bool> &vbMatchesInliers,
                       const cv::Mat &K, vector<cv::Point3f> &vP3D, float th2, vector<bool> &vbGood, float &parallax)
{ 
    // 以第一个相机的光心作为世界坐标系, 定义相机的投影矩阵  相当于本身就是相机系坐标，只需要相机系到像素系
    cv::Mat P1(3,4,             //矩阵的大小是3x4
               CV_32F,          //数据类型是浮点数
               cv::Scalar(0));  //初始的数值是0
    // 将整个K矩阵拷贝到P1矩阵的左侧3x3矩阵，因为 K*I = K
    K.copyTo(P1.rowRange(0,3).colRange(0,3));

    
    cv::Mat P2(3,4,CV_32F);
    R.copyTo(P2.rowRange(0,3).colRange(0,3));   // 复制R
    t.copyTo(P2.rowRange(0,3).col(3));
    P2 = K*P2; 
    
	Triangulate(kp1,kp2,    //特征点
                    P1,P2,      //投影矩阵
                    p3dC1);     //输出，三角化测量之后特征点的空间坐标     
    
    
}

5.3 三角化生成的地图点检验

5.3.1 理论分析

  我们虽然通过三角化成功得到了三维点，但是这些三维点并不都是有效的，需要进行严格的筛查才能作为初始化地图点。

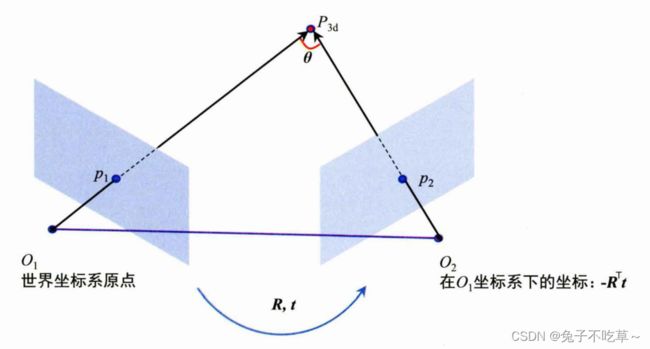
  我们通过判断有效三维点的数目来判断当前位姿是否符合要求。为方便描述，我们把第1、2帧图像称为第1、2个相机。我们把相机1的光轴中心作为世界坐标系原点，从相机1到相机2的位姿记为

$$T_{21}=\left[\begin{array}{cc}{R}_{21}& t_{21}\\ \mathbf{O}& 1\end{array}\right]$$

​ 对$T_{21}$取逆：

$$T_{12}=T_{21}^{-1}=\left[\begin{array}{cc}{\mathbf{R}}_{21}^{\top }& -{\mathbf{R}}_{21}^{\top }{\mathbf{t}}_{21}\\ \mathbf{O}& 1\end{array}\right]$$

  得到

$$\begin{array}{rl}{R}_{12}& =R_{12}^{\top }\\ t_{12}& =-R_{21}^{\top }{t}_{21}\end{array}$$

  所以相机2的光轴中心$O_2$在相机1坐标系下的坐标为$t_{12}=-R_{21}^{\top }{t}_{21}$

  为了求解三维点分别在两个坐标系下和光轴中心的夹角(就是上面图里边的$\theta$)。如果我们要求向量夹角，那么前提是这些向量都在同一个坐标系下。此时$O1$是相机1的光轴中心，也是相机1坐标系原点，$P_{3d}$是相机1坐标系(世界坐标系)下的三维点，这就必须得到$O2$在相机1坐标系下的坐标，也就是我们前面推导的过程。

  还有一点就是，求出来的三维坐标是世界系下的坐标，也就是相机1坐标系下的坐标。

  计算夹角是为了判断三维点的有效性，夹角越大，视差越大，三角化结果越准确。这里其实和双目相机很像，基线和焦距是确定的，视差大（左右匹配点横纵坐标之差），那么说明距离越近，深度值小，视差小，深度值大，那么对于单目三角化这种粗略的估计来说，可信度更低。

条件1：最优解成功三角化点数目明显大于次优解的点数目。
条件2：最优解的视差大于设定点阈值。
条件3：最优解成功三角化点数目大于设定的阈值。
条件4：最优解成功三角化点数目占所有特征点数目的90%以上。

5.3.2 代码分析

/**
 * @brief 用位姿来对特征匹配点三角化，从中筛选中合格的三维点
 * 
 * @param[in] R                                     旋转矩阵R
 * @param[in] t                                     平移矩阵t
 * @param[in] vKeys1                                参考帧特征点  
 * @param[in] vKeys2                                当前帧特征点
 * @param[in] vMatches12                            两帧特征点的匹配关系
 * @param[in] vbMatchesInliers                      特征点对内点标记
 * @param[in] K                                     相机内参矩阵
 * @param[in & out] vP3D                            三角化测量之后的特征点的空间坐标
 * @param[in] th2                                   重投影误差的阈值
 * @param[in & out] vbGood                          标记成功三角化点
 * @param[in & out] parallax                        计算出来的比较大的视差角（注意不是最大，具体看后面代码）
 * @return int 
 */
int Initializer::CheckRT(const cv::Mat &R, const cv::Mat &t, const vector<cv::KeyPoint> &vKeys1, const vector<cv::KeyPoint> &vKeys2,
                       const vector<Match> &vMatches12, vector<bool> &vbMatchesInliers,
                       const cv::Mat &K, vector<cv::Point3f> &vP3D, float th2, vector<bool> &vbGood, float &parallax)
{   

    // 从相机内参数矩阵获取相机的校正参数
    const float fx = K.at<float>(0,0);
    const float fy = K.at<float>(1,1);
    const float cx = K.at<float>(0,2);
    const float cy = K.at<float>(1,2);

    // 特征点是否是good点的标记，这里的特征点指的是参考帧中的特征点
    vbGood = vector<bool>(vKeys1.size(),false);
    //重设存储空间坐标的点的大小
    vP3D.resize(vKeys1.size());

    // 存储计算出来的每对特征点的视差
    vector<float> vCosParallax;
    vCosParallax.reserve(vKeys1.size());

    // Camera 1 Projection Matrix K[I|0]
    // Step 1：计算相机的投影矩阵  
    // 投影矩阵P是一个 3x4 的矩阵，可以将空间中的一个点投影到平面上，获得其平面坐标，这里均指的是齐次坐标。
    // 对于第一个相机是 P1=K*[I|0]
 
    // 以第一个相机的光心作为世界坐标系, 定义相机的投影矩阵  相当于本身就是相机系坐标，只需要相机系到像素系
    cv::Mat P1(3,4,             //矩阵的大小是3x4
               CV_32F,          //数据类型是浮点数
               cv::Scalar(0));  //初始的数值是0
    // 将整个K矩阵拷贝到P1矩阵的左侧3x3矩阵，因为 K*I = K
    K.copyTo(P1.rowRange(0,3).colRange(0,3));
    // 第一个相机的光心设置为世界坐标系下的原点
    cv::Mat O1 = cv::Mat::zeros(3,1,CV_32F);

    // Camera 2 Projection Matrix K[R|t]
    // 计算第二个相机的投影矩阵 P2=K*[R|t]
    cv::Mat P2(3,4,CV_32F);
    R.copyTo(P2.rowRange(0,3).colRange(0,3));   // 复制R
    t.copyTo(P2.rowRange(0,3).col(3));
    // 最终结果是K*[R|t]
    P2 = K*P2;
    // 第二个相机的光心在世界坐标系下的坐标
    cv::Mat O2 = -R.t()*t;

    //在遍历开始前，先将good点计数设置为0
    int nGood=0;

    // 开始遍历所有的特征点对
    for(size_t i=0, iend=vMatches12.size();i<iend;i++)
    {

        // 跳过outliers
        if(!vbMatchesInliers[i])
            continue;

        // Step 2 获取特征点对，调用Triangulate() 函数进行三角化，得到三角化测量之后的3D点坐标
        // kp1和kp2是匹配好的有效特征点
        const cv::KeyPoint &kp1 = vKeys1[vMatches12[i].first];
        const cv::KeyPoint &kp2 = vKeys2[vMatches12[i].second];
        //存储三维点的的坐标
        cv::Mat p3dC1;

        // 利用三角法恢复三维点p3dC1
        Triangulate(kp1,kp2,    //特征点
                    P1,P2,      //投影矩阵
                    p3dC1);     //输出，三角化测量之后特征点的空间坐标        

        // Step 3 第一关：检查三角化的三维点坐标是否合法（非无穷值）
        // 只要三角测量的结果中有一个是无穷大的就说明三角化失败，跳过对当前点的处理，进行下一对特征点的遍历 
        if(!isfinite(p3dC1.at<float>(0)) || !isfinite(p3dC1.at<float>(1)) || !isfinite(p3dC1.at<float>(2)))
        {
            // 其实这里就算是不这样写也没问题，因为默认的匹配点对就不是good点
            vbGood[vMatches12[i].first]=false;
            // 继续对下一对匹配点的处理
            continue;
        }

        // Check parallax
        // Step 4 第二关：通过三维点深度值正负、两相机光心视差角大小来检查是否合法 

        // 得到向量PO1
        cv::Mat normal1 = p3dC1 - O1;
        // 求取模长，其实就是距离
        float dist1 = cv::norm(normal1);

        //同理构造向量PO2
        cv::Mat normal2 = p3dC1 - O2;   // O2已经是相机1系下坐标
        //求模长
        float dist2 = cv::norm(normal2);

        //根据公式：a.*b=|a||b|cos_theta 可以推导出来下面的式子
        float cosParallax = normal1.dot(normal2)/(dist1*dist2);

        // 如果深度值为负值，为非法三维点跳过该匹配点对
        // 视差比较小时，重投影误差比较大。这里0.99998 对应的角度为0.36°,这里实际应该是 cosParallax>0.99998 
        if(p3dC1.at<float>(2)<=0 && cosParallax<0.99998)
            continue;

        // 讲空间点p3dC1变换到第2个相机坐标系下变为p3dC2
        cv::Mat p3dC2 = R*p3dC1+t;  
        //判断过程和上面的相同
        if(p3dC2.at<float>(2)<=0 && cosParallax<0.99998)
            continue;

        // Step 5 第三关：计算空间点在参考帧和当前帧上的重投影误差，如果大于阈值则舍弃
        // 计算3D点在第一个图像上的投影误差
        // 投影到参考帧图像上的点的坐标x,y
        float im1x, im1y;
        // 这个使能空间点的z坐标的倒数
        float invZ1 = 1.0/p3dC1.at<float>(2);
        // 投影到参考帧图像上。因为参考帧下的相机坐标系和世界坐标系重合，因此这里就直接进行投影就可以了
        im1x = fx*p3dC1.at<float>(0)*invZ1+cx;
        im1y = fy*p3dC1.at<float>(1)*invZ1+cy;

        // 参考帧上的重投影误差，这个的确就是按照定义来的
        float squareError1 = (im1x-kp1.pt.x)*(im1x-kp1.pt.x)+(im1y-kp1.pt.y)*(im1y-kp1.pt.y);

        // 重投影误差太大，跳过淘汰
        if(squareError1>th2)
            continue;

        // Check reprojection error in second image
        // 计算3D点在第二个图像上的投影误差，计算过程和第一个图像类似
        float im2x, im2y;
        // 注意这里的p3dC2已经是第二个相机坐标系下的三维点了
        float invZ2 = 1.0/p3dC2.at<float>(2);
        im2x = fx*p3dC2.at<float>(0)*invZ2+cx;
        im2y = fy*p3dC2.at<float>(1)*invZ2+cy;

        // 计算重投影误差
        float squareError2 = (im2x-kp2.pt.x)*(im2x-kp2.pt.x)+(im2y-kp2.pt.y)*(im2y-kp2.pt.y);

        // 重投影误差太大，跳过淘汰
        if(squareError2>th2)
            continue;

        // Step 6 统计经过检验的3D点个数，记录3D点视差角 
        // 如果运行到这里就说明当前遍历的这个特征点对靠谱，经过了重重检验，说明是一个合格的点，称之为good点 
        vCosParallax.push_back(cosParallax);
        //存储这个三角化测量后的3D点在世界坐标系下的坐标
        vP3D[vMatches12[i].first] = cv::Point3f(p3dC1.at<float>(0),p3dC1.at<float>(1),p3dC1.at<float>(2));
        //good点计数++
        nGood++;

        if(cosParallax<0.99998)
            vbGood[vMatches12[i].first]=true;
    }

    // Step 7 得到3D点中较小的视差角，并且转换成为角度制表示
    if(nGood>0)
    {
        // 从小到大排序，注意vCosParallax值越大，视差越小
        sort(vCosParallax.begin(),vCosParallax.end());

        // !排序后并没有取最小的视差角，而是取一个较小的视差角
        // 作者的做法：如果经过检验过后的有效3D点小于50个，那么就取最后那个最小的视差角(cos值最大)
        // 如果大于50个，就取排名第50个的较小的视差角即可，为了避免3D点太多时出现太小的视差角 
        size_t idx = min(50,int(vCosParallax.size()-1));
        //将这个选中的角弧度制转换为角度制
        parallax = acos(vCosParallax[idx])*180/CV_PI;
    }
    else
        //如果没有good点那么这个就直接设置为0了
        parallax=0;

    //返回good点计数
    return nGood;
}