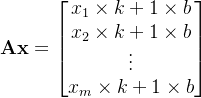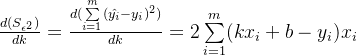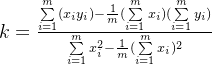普通最小二乘法平面直线回归问题的三种实现(Python)

        最小二乘法（Least Squares Method）由马里·勒让德在1806年发现，距今已经有两个世纪。它是一种数学回归分析工具，可以应用于误差估计、不确定性度量、预测等任务。

        关于用矩阵求解最小二乘法的文章有很多，其中这篇知乎文章总结不错，得到了很多人的点赞。但这篇文章有个缺点，就是跳跃性有点强，比如矩阵求导那里，我看了就很不理解为什么可以这样求导，并且评论中也有人问但作者并没有给出回复。由于对矩阵求导那一步的不理解，所以这导致了我对推导过程的深信不疑，直到看了张贤达《矩阵分析与应用》的普通最小二乘法（讲得不错，值得一看）那部分的内容，我才相信这篇文章的正确性。

        另一方面，知乎上拥有超过8000点赞数的文章（必读）讲得非常好，这篇文章没有使用矩阵求解的方法，而是直接使用更直观的对求和公式求极小值的解法。其实我个人认为这种解法的本质和矩阵解法等价，只是体现形式不一样。

        本篇博客围绕这两篇文章进行一个具体问题的讲解，即使用这两种方法的思想对一个平面直线回归问题进行实现、讲解。另外，本文还提供一种调用sklearn库进行求解的实现方法，以便于作对比分析。

        文章中使用到的完整代码，在上传至CSDN（可免积分下载）。

一、最小二乘法的矩阵形式及其解法

        考虑超定矩阵方程，其中为数据向量，为数据矩阵，并且。假定数据向量存在加性观察误差，即，其中和分别是无误差的数据向量和误差向量。为了抵制误差对矩阵方程求解的影响，引入一个校正向量，并用它去“扰动”有误差的数据向量中的误差，使得，从而实现

的转换。也就是说，如果直接选择校正向量，并且使校正向量“尽可能小”，则可以实现无误差的矩阵方程的求解。

        矩阵方程的这一求解思想可以用下面的优化问题进行描述

        这一方法称为普通最小二乘法，简称最小二乘法。

        事实上，校正向量恰好是矩阵方程两边的误差向量。因此，最小二乘法的核心思想是求出的解向量能够使矩阵方程两边的误差平方和最小化。于是，矩阵方程的普通最小二乘法为

        为了推导的解析解，展开上式，得

        求相对于的导数，得

        其中（矩阵求导相关公式可参考此博客，矩阵转置相关运算可参考百度百科词条-矩阵转置）

        理解了上述的求导过程以后，现在重新回到求导结果，并令其等于零，则有

        换句话说，解必然满足

        严格来说，对于矩阵，该方程的解要分三种情况考虑。本博客主要针对第一种情况展开讲解和实现，对于第二种和第三种情况，由于博主个人知识有限因此不作进一步的讨论，感兴趣的同学可自行查阅相关资料。

        (1) 且，此时方程有唯一解，求解时可直接利用该等式；

        (2) 且，此时解，其中代表矩阵的Moore-Penrose矩阵；

        (3) 且，这种情况下由的不同解均得到相同的值。虽然数据向量可以提供有关的某些信息，但是无法区分对应于相同值的各个不同的未知参数向量。因此称这样的参数向量是不可辨识的。（可以认为无解）

二、平面直线回归问题

        以上是最小二乘法的理论部分，虽然数学符号很多，看起来似乎特别难的样子，但还是要静下心来慢慢阅读理解。这里，我将按照自己的理解，针对最小二乘法举一个具体的问题和求解案例。

        集合的元素定义为二维空间坐标。假设集合

        我们的问题是找到一条直线，使得集合中每组数据中对的预测值到的距离之和最小。如果把最小二乘法当作一个黑盒，那么输入的就是一组二维坐标数据，而输出的数据就是找到的这条直线的斜率和截距。

三、用普通最小二乘法之矩阵解法求解平面直线回归问题

        假设这条直线的方程是，那么我们所需求解的参数则是和，因此。输入的一组数据为，其中。那么

，，

        而我们的目标是使得

        因此解。

       可能有的同学会问，还没有解释呢？在这里的值为2。实际上，对于一个数据，可以认为前者是一个样本，这个样本具有维数据（可以认为是），后者是该样本所对应的标签，或者认为是预测任务中所需要预测的值，但绝不是样本的第二维数据，这个不要混淆。

       Python3实现代码：

import numpy as np

# 手写最小二乘法实现平面直线回归问题（算法：矩阵解法）
def diy_lsm_by_mat(data):
    # 对于二维坐标点集合{(x1, y1), (x2, y2), ..., (xm, ym)}
    # 输入的数据格式为[x1, x2, ..., xm], [y1, y2, ..., ym]
    x, y = data
    mat_l = np.mat(np.ones((len(x), 1)))            # 生成m×1的全一矩阵
    mat_a = np.hstack((np.mat(x).T, mat_l))         # 得到矩阵A (m×2)
    mat_b = np.mat(y).T                             # 得到矩阵b (m×1)
    mat_x = (mat_a.T * mat_a).I * mat_a.T * mat_b   # 利用矩阵求解的公式直接求解
    # 得到求解结果
    k, b = mat_x[0, 0], mat_x[1, 0]
    # 输出求解结果
    print(k, b)
    # 返回求解结果
    return k, b

四、用求和公式解决平面直线回归问题

        集合的元素定义为二维空间坐标。假设集合

，

        我们的问题是找到一条直线，使得

        最小，其中。对求偏导（建议展开成各项相加的形式求偏导），得

        令第二个偏导等于零，有

        进一步得到

        再令第一个偏导等于零，有

        进一步得到

        再进行化简，得

        此时，把的代入等式，化简得到

        最后，把的值代入

        即可求得系数。

        Python3实现代码：

# 手写最小二乘法实现平面直线回归问题（算法：求和公式解决）
def diy_lsm_by_sum(data):
    # 对于二维坐标点集合{(x1, y1), (x2, y2), ..., (xm, ym)}
    # 输入的数据格式为[x1, x2, ..., xm], [y1, y2, ..., ym]
    x, y = data
    m = len(x)          # 获取坐标点的个数
    sum_xi = 0          # 用于xi求和的变量
    sum_yi = 0          # 用于yi求和的变量
    sum_xi_xi = 0       # 用于xi × xi求和的变量
    sum_xi_yi = 0       # 用于xi × yi求和的变量
    for i in range(m):
        sum_xi = sum_xi + x[i]                  # 对每个xi求和
        sum_yi = sum_yi + y[i]                  # 对每个yi求和
        sum_xi_xi = sum_xi_xi + x[i] * x[i]     # 对每个xi × xi求和
        sum_xi_yi = sum_xi_yi + x[i] * y[i]     # 对每个xi × yi求和
    # 利用求解公式求得k
    k = (sum_xi_yi - (1 / m) * sum_xi * sum_yi) / (sum_xi_xi - (1 / m) * sum_xi ** 2)
    # 利用求解公式求得b
    b = (sum_yi - k * sum_xi) / m
    # 输出求解结果
    print(k, b)
    # 返回求解结果
    return k, b

五、调用sklearn库求解

        sklearn也可以解决上述问题，且它的泛化能力、通用性比我写的代码强大得多。不过它是一个黑盒，我们很难想象它的内部是如何计算得来的。但就上述的问题而言，我觉得应该和以上的两种计算思想大同小异。黑盒意味着只要你提供一个输入，经过这个黑盒的计算后就会得到一个输出。换句话说，我们需要把一组坐标点转化为sklearn的输入数据即可。具体使用方法如下：

import numpy as np
from sklearn import linear_model

# 调用sklearn中最小二乘法实现平面直线回归问题
def sof_lsm_by_skl(data):
    # 对于二维坐标点集合{(x1, y1), (x2, y2), ..., (xm, ym)}
    # 输入的数据格式为[x1, x2, ..., xm], [y1, y2, ..., ym]
    x, y = data
    # 将输入的数据转化为sklearn能接受的输入
    nx = np.array(x).reshape(-1, 1)
    ny = np.array(y).reshape(-1, 1)
    # 调用sklearn的线性回归模型
    lr = linear_model.LinearRegression()
    # 调用sklearn求解（黑盒计算）
    lr.fit(nx, ny)
    # 得到求解结果
    k, b = lr.coef_[0, 0], lr.intercept_[0]
    # 输出求解结果
    print(k, b)
    # 返回求解结果
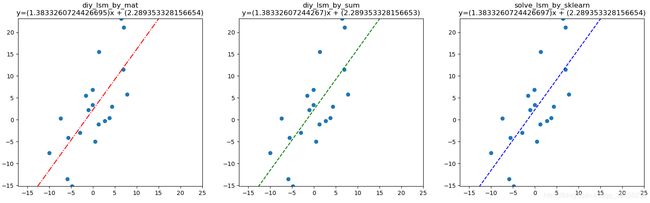
    return k, b

六、三种方法的求解结果

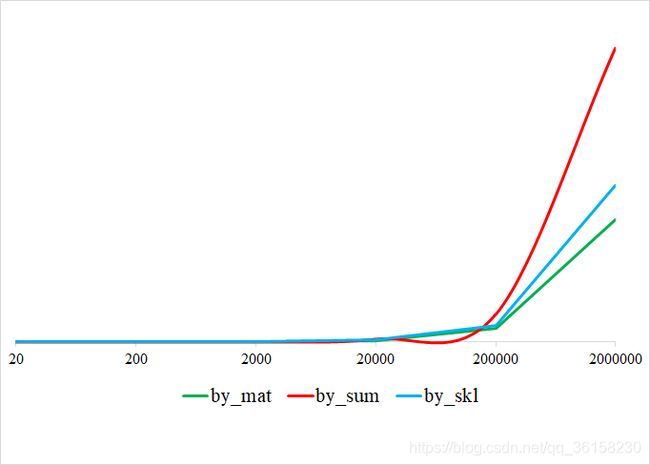
        三种求解结果基本上一样，只是在求解精度上有非常非常非常小的差距，几乎可以忽略不计。

        从运行时间上看，使用矩阵进行求解的速度更快，求和公式求解更慢。以下的图通过进行6次实验得出，分别指定坐标点的个数为20, 200, 2000, 20000, 200000, 2000000，然后得到以下的运行时间，其中纵坐标是运行时间。这说明了矩阵计算确实高效。

七、总结

        至此，已经介绍了最小二乘法的矩阵求解理论，并且通过一个非常具体的例子进行了三种方式的实现以及实验的对比。但最小二乘法的应用不仅仅局限于解决平面直线的线性回归问题，这是应该注意的地方。学习和掌握这个基础的方法还是很有必要的，这样在遇到最小二乘法的拓展或变体时可以轻松应对。

        在学习最小二乘法的过程中，我发现使用最小二乘法求解时它是直接可以通过公式计算出来，也就是说，它不像梯度下降那样，需要一步一步迭代（或者说训练）。这说明使用最小二乘法求解速度很快。

        但是最小二乘法也存在一些不足之处。当矩阵不可逆时，这个时候它就不能够使用；另外，当特征数的维数特别高时，用最小二乘法计算的话其计算量会特别大，这时就不适合使用最小二乘法；如果拟合函数不是线性的，也无法使用最小二乘法，需要通过一些技巧转化为线性才能使用。以上缺点在这篇知乎文章也讲到。

        怎么说呢，学习这个最小二乘法的时候，感觉学到蛮多东西的，对矩阵的运算，特别是矩阵求导，掌握了不少，受益良多。

        码字之余，难免疏漏，若有不对，敬请留言，批评改正。

参考资料

        1. Kaare Brandt Petersen & Michael Syskind Pedersen，Matrix Cookbook

        2. 张贤达，矩阵分析与应用（第2版）

        3. 知乎-马同学，最小二乘法的本质是什么？

        4. 知乎-Eureka，最小二乘法（least sqaure method）

        5. CSDN-Cyril_KI，机器学习之linear_model(普通最小二乘法手写+sklearn实现+评价指标)

        6. 其他忘了记录的参考...