力扣热题100道-矩阵篇
矩阵
73.矩阵置零
给定一个 m x n 的矩阵,如果一个元素为 0 ,则将其所在行和列的所有元素都设为 0 。请使用 原地 算法**。**
示例 1:

输入:matrix = [[1,1,1],[1,0,1],[1,1,1]]
输出:[[1,0,1],[0,0,0],[1,0,1]]
示例 2:

输入:matrix = [[0,1,2,0],[3,4,5,2],[1,3,1,5]]
输出:[[0,0,0,0],[0,4,5,0],[0,3,1,0]]
/*
思路:采用两个标记数组
*/
class Solution {
public:
void setZeroes(vector<vector<int>>& matrix) {
int m=matrix.size();
int n=matrix[0].size();
vector<int> row(m,1),col(n,1);
for(int i=0;i<m;i++){
for(int j=0;j<n;j++){
if(matrix[i][j]== 0){
row[i]=0;
col[j]=0;
}
}
}
for(int i=0;i<m;i++){
for(int j=0;j<n;j++){
if(!row[i] || !col[j]){
matrix[i][j]=0;
}
}
}
}
};
54.螺旋矩阵
给你一个 m 行 n 列的矩阵 matrix ,请按照 顺时针螺旋顺序 ,返回矩阵中的所有元素。
示例 1:
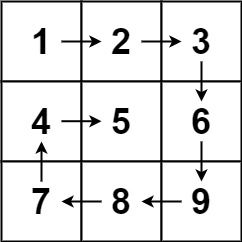
输入:matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出:[1,2,3,6,9,8,7,4,5]
示例 2:
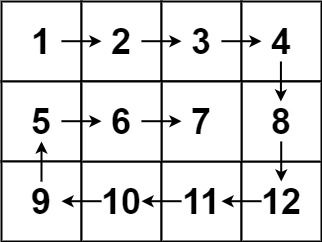
输入:matrix = [[1,2,3,4],[5,6,7,8],[9,10,11,12]]
输出:[1,2,3,4,8,12,11,10,9,5,6,7]
/*
思路 从右下左上的顺序轮转,用4个变量记录边界
*/
class Solution {
public:
vector<int> spiralOrder(vector<vector<int>>& matrix) {
//从右下左上四个方向遍历
int l=0,r=matrix[0].size()-1;
int u=0,d=matrix.size()-1;
vector<int> res;
while(true){
for(int j=l;j<=r;j++){ //从左到右
res.push_back(matrix[u][j]);
}
if(++u > d) break;
for(int i=u;i<=d;i++){ //从上到下
res.push_back(matrix[i][r]);
}
if(--r <l) break;
for(int i=r;i>=l;i--) //从右到左
{
res.push_back(matrix[d][i]);
}
if(--d < u) break;
for(int i=d;i>=u;i--) //从下到上
{
res.push_back(matrix[i][l]);
}
if(++l > r) break;
}
return res;
}
};
48.旋转图像
给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。
你必须在** 原地** 旋转图像,这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。
示例 1:
输入:matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出:[[7,4,1],[8,5,2],[9,6,3]]
示例 2:
输入:matrix = [[5,1,9,11],[2,4,8,10],[13,3,6,7],[15,14,12,16]]
输出:[[15,13,2,5],[14,3,4,1],[12,6,8,9],[16,7,10,11]]
/**
思路:先水平旋转 后对角线旋转
**/
class Solution {
public:
void rotate(vector<vector<int>>& matrix) {
int n=matrix.size();
//先翻转
for(int i=0;i<n/2;i++){
for(int j=0;j<n;j++){
swap(matrix[i][j],matrix[n-i-1][j]);
}
}
//后主对角线交换
for(int i=0;i<n;i++)
for(int j=i+1;j<n;j++)
swap(matrix[i][j],matrix[j][i]);
}
};
240.搜索二维矩阵Ⅱ
编写一个高效的算法来搜索 *m* x *n* 矩阵 matrix 中的一个目标值 target 。该矩阵具有以下特性:
- 每行的元素从左到右升序排列。
- 每列的元素从上到下升序排列。
示例 1:
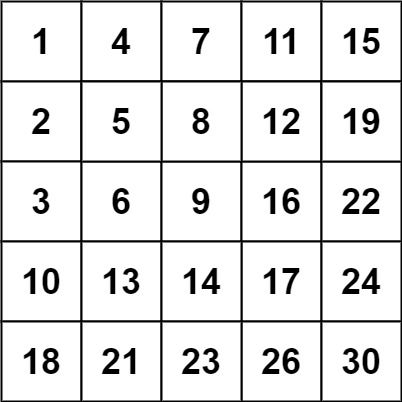
输入:matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 5
输出:true
示例 2:
输入:matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 20
输出:false
//思路:
/*
从第一行最后一个开始,target小就往左,target大就往下
*/
class Solution {
public:
bool searchMatrix(vector<vector<int>>& matrix, int target) {
int m=matrix.size();
int n=matrix[0].size();
int x=0,y=n-1,num;
while(x<m && y>=0){
num=matrix[x][y];
if(num>target) y--;
else if(num == target) return true;
else if(num < target) x++;
}
return false;
}
};