【LeetCode题目拓展】第207题 课程表 拓展(拓扑排序、Tarjan算法、Kosaraju算法)
文章目录
-
- 一、拓扑排序题目
- 二、题目拓展
-
- 1. 思路分析
- 2. tarjan算法
- 3. kosaraju算法
一、拓扑排序题目
最近在看一个算法课程的时候看到了一个比较好玩的题目的扩展,它的原题如下:
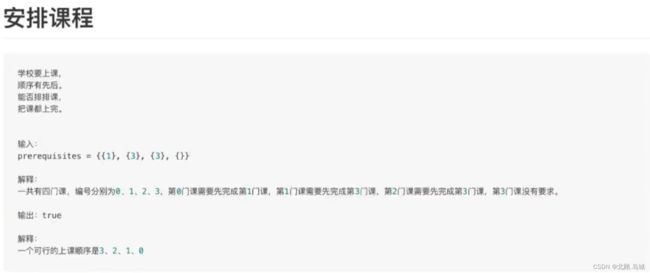
对应的LeetCode题目为 207. 课程表
这个题目本身来说比较简单,就是一道标准的拓扑排序题目,解法代码如下:
import java.util.ArrayList;
import java.util.LinkedList;
import java.util.List;
import java.util.Queue;
public class Solution {
public boolean scheduleCourses(int[][] prerequisites) {
// 记录每个节点的入度
int[] degree = new int[prerequisites.length];
// 记录每个节点是哪些节点的前置节点
List<Integer>[] neighbors = new List[prerequisites.length];
// 记录当前可以选择的节点
Queue<Integer> available = new LinkedList<>();
for (int i = 0; i < prerequisites.length; i++) {
degree[i] = prerequisites[i].length;
neighbors[i] = new ArrayList<>();
if (degree[i] == 0) {
available.offer(i);
}
}
for (int i = 0; i < prerequisites.length; i++) {
for (int to : prerequisites[i]) {
neighbors[to].add(i);
}
}
int count = 0;
while (!available.isEmpty()) {
// 1. 取出available中一个节点
// 2. 遍历该节点的邻居节点
// a. 将该邻居节点的入度减一
// b. 若此时邻居节点的入度为0,加入available中
// 3. 处理节点数count加一
int cur = available.poll();
for (int to: neighbors[cur]) {
degree[to]--;
if (degree[to] == 0) {
available.offer(to);
}
}
count++;
}
return count == prerequisites.length;
}
}
二、题目拓展
这道题目整体难度不大,但是课程里提出了对于该题目的拓展非常有意思。
题目拓展:假如学生有同时上多门课的能力,那么是否可以根据他最多能同时上课的数量,来判断对于指定的课程安排他是否可以完成。
1. 思路分析
初看这个拓展时,我的想法是在有向图里找环的方式来实现,比如找到整个有向图中包含节点数目最多的环,判断这个数目是否超过了该同学最多能同时上课的数量。但这种方式有一个比较大的问题,就是如何定义什么是环,以及该定义下的环是否满足需要。根据这两个问题,我举出了如下两个图:

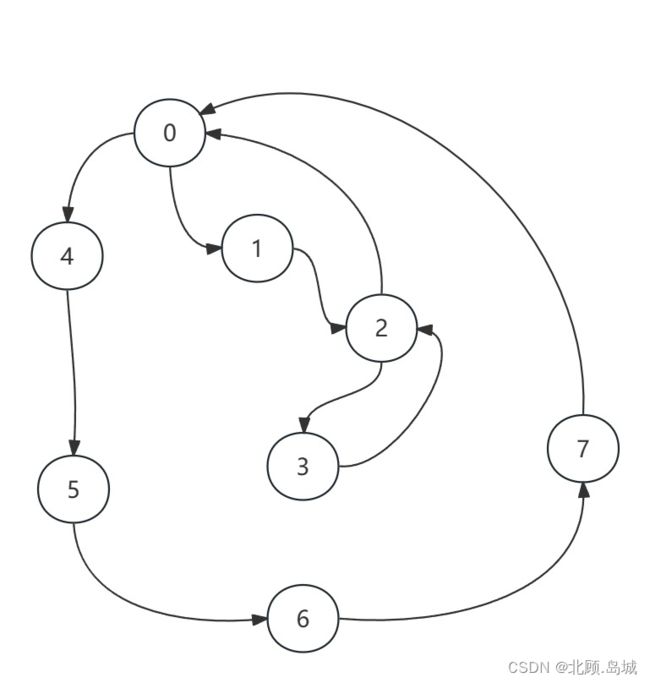
可以看到,对于第一个图来说,它可以说包含3个环,这种情况下该以哪个环的节点数来度量呢?对于第二个图,两个环共用了一个节点,此时只计算一个环的节点数并不能满足题目的需求。
此时仔细观察图二中的这种场景,我发现只有这两个环都计算节点数然后与可以最大同时上课数比较才成立。结合图一,可以得出一个结论,即当图中一个节点与另一个节点可以互相到达时,它们需要被计算在一起。这不正好就是有向图的强连通分量的定义吗?
于是,这个问题就转换成了,求一个有向图中包含节点数最大的连通分量的节点数。整个思路豁然开朗了。(由此可以看出,拿到一些特化的问题时把问题迁移到一种常识性问题是非常重要的!)
根据这种思路,我们需要求有向图中规模最大的连通分量的节点数,并且把它和学生最大同时上课数进行比较,就可以得到答案了。
详细图示如下:

将每一个强连通分量视为学生需要同时上的课程,即可以得到一个强连通分量缩点的拓扑排序,之后学生可以按照正常的拓扑排序顺序对缩点进行上课即可,如下所示:
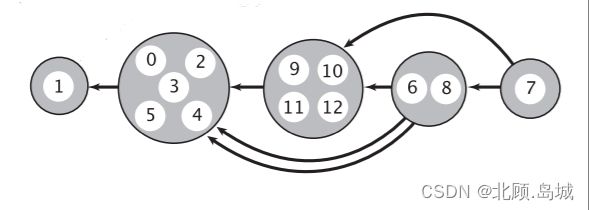
求解有向图中的强连通分量问题一般有两种算法,tarjan算法和kosaraju算法,此处不赘述两种算法的细节,感兴趣的可以自行搜索,此处只把各自解法列在下方。
2. tarjan算法
import java.util.ArrayList;
import java.util.LinkedList;
import java.util.List;
import java.util.Stack;
public class TarjanSolution {
// 图的邻接表表示形式,记录每个节点是哪些节点的前置节点
private List<Integer>[] neighbors;
private int skill;
private int[] dfn;
private int[] low;
private int idx;
private Stack<Integer> stack;
private boolean[] isInStack; // 用于快速判断是否在栈中
public boolean scheduleCourses(int[][] prerequisites, int skill) {
if (skill < 1) {
return false;
}
this.skill = skill;
// 初始化相关存储结构
initGraph(prerequisites);
// 最大连通分量的节点数
return tarjan();
}
private void initGraph(int[][] prerequisites) {
neighbors = new List[prerequisites.length];
for (int i = 0; i < prerequisites.length; i++) {
neighbors[i] = new LinkedList<>();
}
for (int i = 0; i < prerequisites.length; i++) {
for (int to : prerequisites[i]) {
neighbors[to].add(i);
}
}
}
private boolean tarjan() {
this.dfn = new int[neighbors.length];
this.low = new int[neighbors.length];
this.idx = 0;
this.isInStack = new boolean[neighbors.length];
this.stack = new Stack<Integer>();
for (int i = 0; i < neighbors.length; ++i) {
if (dfn[i] == 0) {
if (!tarjanRecursion(i)) { // 如果已经失败,则提前结束
return false;
}
}
}
return true;
}
private boolean tarjanRecursion(int cur) {
// 入栈
stack.push(cur);
isInStack[cur] = true;
//初始化当前节点的时间戳
dfn[cur] = low[cur] = ++idx;
// 遍历当前节点的邻居节点,共3类:1. 没被找过的;2. 在栈里的;3. 已经构成联通分量的(这种直接跳过即可)
for (int neighbor: neighbors[cur]) {
// 如果没被找过
if (dfn[neighbor] == 0) {
if (!tarjanRecursion(neighbor)) { // 如果已经失败,则提前结束
return false;
}
low[cur] = Math.min(low[cur], low[neighbor]);
} else if (isInStack[neighbor]) { // 在栈里
low[cur] = Math.min(low[cur], dfn[neighbor]);
}
}
int connectedComponentNodeNum = 0;
// 若dfn==low,则当前已找到一个强连通分量,该分量节点为当前节点到栈顶的所有节点
if (dfn[cur] == low[cur]) {
while (cur != stack.peek()) { // 将所有非当前节点退栈
int tmp = stack.pop();
isInStack[tmp] = false;
if (++connectedComponentNodeNum > skill) {
return false;
}
}
// 把当前节点退栈
stack.pop();
isInStack[cur] = false;
if (++connectedComponentNodeNum > skill) {
return false;
}
}
return true;
}
}
3. kosaraju算法
import java.util.LinkedList;
import java.util.List;
import java.util.Stack;
public class KosarajuSolution {
// 图的邻接表表示形式,记录每个节点是哪些节点的前置节点
private List<Integer>[] neighbors;
// 图的逆邻接表表示形式,记录每个节点是哪些节点的后置节点
private List<Integer>[] rneighbors;
private int skill;
private boolean[] visited;
private Stack<Integer> stack;
public boolean scheduleCourses(int[][] prerequisites, int skill) {
if (skill < 1) {
return false;
}
this.skill = skill;
// 初始化相关存储结构
initGraph(prerequisites);
// 最大连通分量的节点数
return kosaraju();
}
private void initGraph(int[][] prerequisites) {
neighbors = new List[prerequisites.length];
rneighbors = new List[prerequisites.length];
for (int i = 0; i < prerequisites.length; i++) {
neighbors[i] = new LinkedList<>();
rneighbors[i] = new LinkedList<>();
}
for (int i = 0; i < prerequisites.length; i++) {
for (int to : prerequisites[i]) {
neighbors[to].add(i);
rneighbors[i].add(to);
}
}
}
private boolean kosaraju() {
this.visited = new boolean[neighbors.length];
this.stack = new Stack<Integer>();
for (int i = 0; i < neighbors.length; ++i) { // 遍历正向图,记录出栈顺序
if (!this.visited[i]) {
kosarajuDfs1(i);
}
}
while (!stack.isEmpty()) { // 从出栈最晚的节点开始,dfs遍历反向图
int cur = stack.pop();
if (this.visited[cur]) {
if (kosarajuDfs2(cur) > skill) // 提前结束
return false;
}
}
return true;
}
private void kosarajuDfs1(int cur) {
this.visited[cur] = true;
for (int next: this.neighbors[cur]) {
if (!this.visited[next]) {
kosarajuDfs1(next);
}
}
stack.push(cur);
}
private int kosarajuDfs2(int cur) {
this.visited[cur] = false;
int count = 1;
for (int pre: this.rneighbors[cur]) {
if (this.visited[pre]) {
if (count > this.skill) return count; // 提前结束
count += kosarajuDfs2(pre);
}
}
return count;
}
}