数据结构与算法(1)

数据结构

数据结构指的是数据的组织、管理和存储格式，可以高效地访问和修改数据。常见的数据结构如下表：

类型	举例
线性结构	数组、链表、栈、队列、哈希表
树	二叉树、二叉堆……
图	单向图、双向图……
其他	跳表、哈希链表、位图……

数组 array

数组：在内存上连续的顺序存储，访问效率高，不便于插入、删除和扩展。array比较适用于读操作多、写操作少的场景。

/****************************************
*
* typename array[] = {};
*  _________________________________________________________
* |array[0] | array[1] | array[2] | array[3] | ... |
*  ---------------------------------------------------------
*
*/

链表 linked list

物理上不连续、非顺序的存储的结构，由一个一个相连的节点（包含数据、指针）组成。节点的指针(next)指向其后继节点。

/**************************************************************
*
*      _________    -->  ________    -->  ________
*     |   data  |   |   |  data  |   |   |  data  |
*     |---------    |   |--------|   |   |--------|
*     |   next  |---|   |  next  |---|   |  NULL  |
*      ---------         --------         --------
*
*/

双向链表 doubly linked list

双向链表的节点包含两个指针（prev：指向前驱节点的指针，next：指向后继节点的指针）

栈 stack

栈：一种先进后出(First In Last Out, FILO)，看上去像一个桶的线性结构。

栈即可以用数组来实现，也可以用链表来实现。栈顶(top)先出栈，栈底(bottom)后出栈。

队列 queue

队列：就像去食堂排队打饭一样的先进先出(First In First Out, FIFO)的线性数据结构。队头(front)先出队，队尾(rear)后出队。

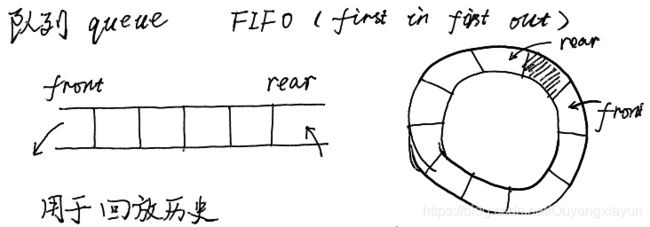
上图右侧是表示一个循环队列，使用数组即可以很方便的表示。

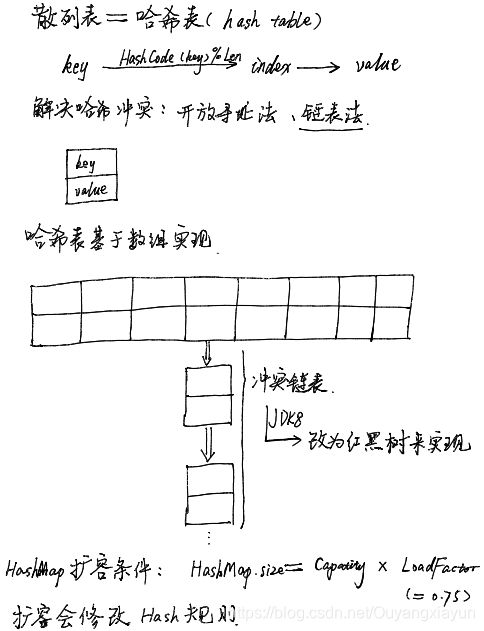
哈希表 hash table(散列表)

树 tree

树，多个节点的集合，包含以下特性：

• 有且仅有一个节点称为根（root）节点
• 每个节点又可以包含多个子节点，没有子节点的节点称为叶子（leaf）节点
• 任意一个节点只能是某一个节点(称为父节点(parent))的子节点，即树支只能分叉，不能生长到一起；即任意节点只能有一个父节点
• 从根节点（root）开始，到最后一批叶子节点（leaf）的代数，称为树的深度或高度或层数（h）
• 同级或同一代或同一层的所有节点互相称为兄弟节点（sibling）

整个树有点像一个家谱图。有父亲parent，孩子child，兄弟sibling等节点关系。

二叉树

二叉树的存储

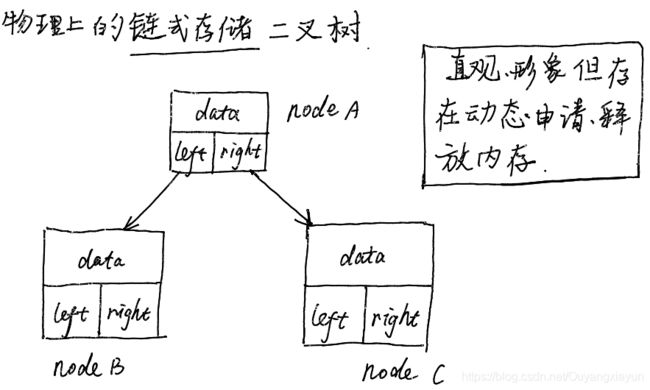
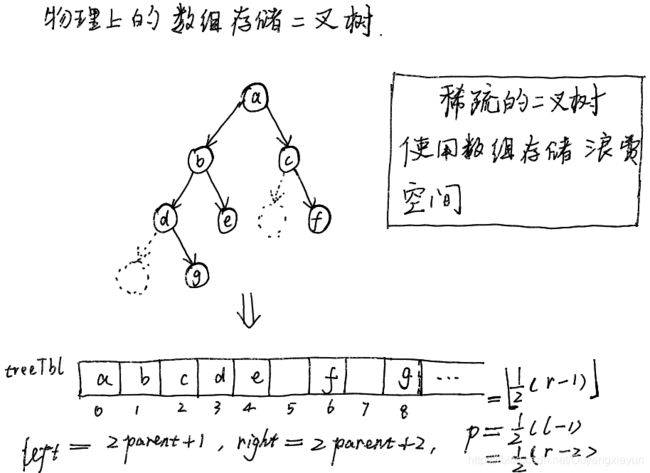
链式存储二叉树，直观形象，代码简单，需要动态申请内存来存储节点；
使用数组来存储二叉树，访问效率高，但存储稀疏的二叉树则非常浪费存储空间。

二叉查找树（二叉排序树）binary search tree

二叉查找树：左子树所有节点均小于根节点的值；右子树所有节点均大于树节点的值；且左、右子树均是二叉查找树。

二叉树的自平衡

二叉树新增节点的插入需要根据新插入的节点调整整个二叉树以保证二叉树维护相对的平衡而不会变成一条线性的链表。

二叉树的遍历

• 深度优先遍历(DFS)：前序遍历、中序遍历、后序遍历
• 广度优先遍历(BFS)：层序遍历

前序遍历

root—>left sub tree —> right sub tree

中序遍历

left sub tree —> root —> right sub tree

后序遍历

left sub tree —> right sub tree —> root

以上三种遍历均使用递归来实现，则只在词句顺序上有区别；使用递归来实现也可以改为使用stack来实现。

层序遍历

借助队列，逐层入队出队，出队时出队节点的子节点按序入队，队列为空，则树遍历结束。

二叉堆

二叉堆，一种具有自平衡能力的完全二叉树。
最大堆：
$\forall parent,parent>=leftchild,parent>=rightchild$
最小堆：
$\forall parent,parent<=leftchild,parent<=rightchild$

二叉堆的自我调整

二叉堆在构建、插入节点、删除节点的时候都需要调整节点的顺序。

比如，在最小堆中，插入新的节点，可以从最后的位置，将新插入的节点与其父节点比较，只要比父节点小，则将其与父节点交换。依次直到“上浮”到能到的最“顶端”的位置。

同样的，在最小堆中，要删除一个节点，则将最后的节点放到删除节点的位置，再依次“下沉”到最“底端”的位置。

要构建一棵二叉堆，则将所有非叶子节点依次“下沉”。

插入、删除二叉堆中的一个节点的时间复杂度均为$O(logn)$，构建二叉堆的时间复杂度为$O(n)$。

二叉堆使用数组（而不是链表）来存储更为简单。

优先队列

最大优先队列，无论入队顺序如何，都是最大元素先出队。

最小优先队列，无论入队顺序如何，都是最小元素先出队。

使用二叉堆来实现优先队列，入队即插入新节点，出队即删除堆顶节点，时间复杂度均为$O(logn)$。

数据存储的物理结构与逻辑结构

逻辑结构	线性结构(顺序表、栈、队列)	非线性结构（树、图）
物理结构	顺序存储（数组）	链式存储（链表）

算法

算法，主要考虑的时间复杂度（基本操作的执行次数）和空间复杂度（算法所占用存储空间的规模）。

一般用大$O$表示法来表示。常见的量级比较：
$$O(1)<O(logn)<O(n)<O(nlogn)<O(n^2)$$

我们将在下一篇中开始复习相关的算法。