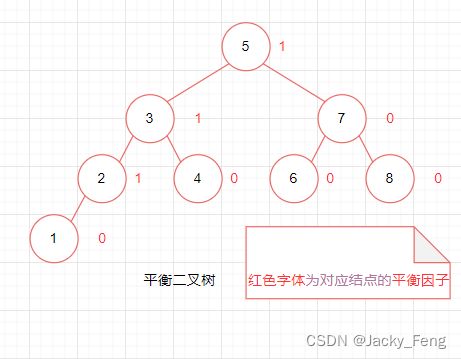
【数据结构】平衡二叉树

导语

对于二叉搜索树 而言，它的 增、 删 、 改 、 查  的时间复杂度为 O() ~ O(n) 。原因是最坏情况下，二叉搜索树会退化成 线性表  。换言之，树的高度决定了它插入、删除和查找的时间复杂度。
为了对上述缺点进一步优化，设计了一种高度始终能够接近 O() 的 树形  的数据结构，它既有链表的快速插入与删除的特点，又有顺序表快速查找的优势。它就是：平衡二叉树 。

---

 一、平衡二叉树基本概念

1、平衡二叉树的定义

平衡二叉树（AVL树），是一种平衡(balanced)的二叉搜索树(binary search tree, 简称为BST)。由两位科学家在1962年发表的论文《An algorithm for the organization of information》当中提出，作者是发明者G.M. Adelson-Velsky和E.M. Landis。它具有以下两个性质：

• 空树是平衡二叉树
• 任意一个结点的key，比它的左孩子key大，比它的右孩子key小；
• 任何一个结点的左子树与右子树都是平衡二叉树，并且高度之差的绝对值不超过 1。

2、树的高度

一棵树的高度，是指从树根结点到达最远的叶子结点的路径上经过的结点数。所以，求树的高度我们可以采用递归的方式。主要有以下三种情况：

1）空树的树高为 0；

2）叶子结点的树高为 1；

3）其它结点的树高，等于左右子树树高的大者加 1；

3、平衡因子

二叉树上的结点的 左子树高度 减去 右子树高度 的值称为 平衡因子，即 BF（Balance Factor）。 根据平衡二叉树的定义，树上所有结点的平衡因子只可能是 -1、0 和 1。即只要二叉树上有一个结点的平衡因子的绝对值大于 1，则该二叉树就是不平衡的。

二、平衡二叉树存储结构

对于平衡二叉树，首先是二叉搜索树，所以会有 左右孩子指针 和 数据域，然后特殊之处是需要平衡因子，而平衡因子可以通过节点树的高度来计算，所以需要加一个 高度。

struct TreeNode {
	int val;
	struct TreeNode* left;
	struct TreeNode* right;
	int height;
	TreeNode(int x, int h = 1) :val(x), left(nullptr), right(nullptr), height(h){}
};

三、平衡二叉树基本接口

1、获取树高

int AVLGetHeight(TreeNode* node)
{
	if (node == nullptr) {
		return 0;
	}
	return node->height;
}

获取树高期望做到 O(1) 的时间复杂度，height 字段是需要存储在结点上的，并且每次树的 插入、删除 操作都需要更新这个值。

空结点的树高为 0，其它结点的树高可以直接通过获取树结点结构体的成员变量height 字段快速获取。

2、计算树高

每次对树进行插入、删除操作，对树的原结点高度会有影响，所以需要重新计算，更新这个值。

//计算树高（结点增删需要重新计算树高）
void AVLCalcHeight(TreeNode* node) {
	if (nullptr == node) {              
		return ;
	}                                
	node->height = 1 + std::max(AVLGetHeight(node->left), AVLGetHeight(node->right));
}

 3、获取平衡因子

同理，每次对树进行插入、删除操作，对树的原结点的平衡因子也会有影响，所以也需要重新计算这个值。

//获取平衡因子
int AVLGetBalanceFactor(TreeNode* node) {
	if (node == nullptr)
		return 0;                                                
	return AVLGetHeight(node->left) - AVLGetHeight(node->right); 
}

4、旋转操作

每次对树进行插入、删除操作，可能会引起树的平衡，此时就需要通过旋转操作来使树重新回到平衡状态。

假设本来这棵树是平衡的，在我们在插入一个结点以后，导致了这棵树的不平衡，那么必然是这棵树根结点的平衡因子从 +1 变成了 +2，或者从 -1 变成了 -2 。我们来分别讨论这两种情况。

实际上，总共有四种情况：

1）LL（往左子树的左子树插入一个结点），根结点的平衡因子 +2，左子树根结点平衡因子 +1；

2）RR（往右子树的右子树插入一个结点），根结点的平衡因子 -2，右子树根结点平衡因子 -1；

3）LR（往左子树的右子树插入一个结点），根结点的平衡因子 +2，左子树根结点平衡因子 -1；

4）RL（往右子树的左子树插入一个结点），根结点的平衡因子 -2，右子树根结点平衡因子 +1；

结论：+1 变成 +2 的情况发生在 LL 和 LR，即往当前树的左子树插入一个结点的情况；-1 变成 -2 的情况发生在 RL 和 RR，即往当前树的右子树插入一个结点的情况。

（1） LL

LL，即往左子树的左子树插入一个结点。这种情况下，如果树出现了不平衡的情况，根结点的当前平衡因子一定是 +2。

如上图所示，在左子树插入T5结点后，平衡二叉树的平衡状态被打破，要想回到平衡状态需要对树进行一个右旋操作。

如图所示，以左子树根结点T1作支点右旋后，重新达到平衡。总共有以下关系发生了变化：

（1）T1变成了新的树根

（2）T和T1父子关系发生了交换

（3）T4的父节点由T1变为T

右旋源码

//右旋
TreeNode* RRotate(TreeNode* T)
{
	TreeNode* LNode = T->left;
	T->left = LNode->right;
	LNode->right = T;
	AVLCalcHeight(T);
	AVLCalcHeight(LNode);
	return LNode;
}

经过右旋后，只有T1和T的高度发生了变化，所以需要对它们重新计算高度。

LL型旋转处理

// LL 型右旋处理
TreeNode* AVLTreeLL(TreeNode* T) {
	return RRotate(T);
}

（2）RR

RR，即往右子树的右子树插入一个结点。这种情况下，如果树出现了不平衡的情况，根结点的当前平衡因子一定是 -2。

如上图所示，在右子树插入T5结点后，平衡二叉树的平衡状态被打破，要想回到平衡状态需要对树进行一个左旋操作。

如图所示，以右子树根结点T2作支点左旋后，重新达到平衡。总共有以下关系发生了变化：

（1）T2变成了新的树根

（2）T和T2父子关系发生了交换

（3）T3的父节点由T2变为T

左旋源码

//左旋
TreeNode* LRotate(TreeNode* T)
{
	TreeNode* RNode = T->right;
	T->right = RNode->left;
	RNode->left = T;
	AVLCalcHeight(T);
	AVLCalcHeight(RNode);
	return RNode;
}

RR型处理源码

//RR型左旋处理
TreeNode* AVLTreeRR(TreeNode* T) {
	return LRotate(T);
}

（3）LR

LR，即往左子树的右子树插入一个结点。这种情况下，如果树出现了不平衡的情况的话，根结点的当前平衡因子一定是 +2。

假设以左子树的右子树T4结点为支点，对左子树进行一次左旋操作，得到如下图所示：

可以看到，经过一次左旋得到新树，形状和LL型一致，所以接下来再按照型LL处理，再右旋一次即可达到平衡状态

所以对于LR型的处理主要有两步：

（1）对树T的左子树进行左旋

（2）对树T进行右旋

LR型处理源码

//LR型左旋+右旋处理
TreeNode* AVLTreeLR(TreeNode* T) {
	T->left = LRotate(T->left);   //左旋处理并修改T的左指针指向
	return RRotate(T);    //对T进行右旋处理       
}

 （4）RL

RL，即往右子树的左子树插入一个结点。这种情况下，如果树出现了不平衡的情况的话，根结点的当前平衡因子一定是 -2。

假设以右的左子树T4结点为支点，对右子树进行一次右旋操作，得到如下图所示：

可以看到，经过一次右旋得到新树，形状和RR型一致，所以接下来再按照型RR型处理，再左旋一次即可达到平衡状态

所以对于RL型的处理主要有两步：

（1）对树T的右子树进行右旋

（2）对树T进行左旋

RL型处理源码

//RL型右旋+左旋处理
TreeNode* AVLTreeRL(TreeNode* T) {
	T->right = RRotate(T->right);    // 右子树进行右旋处理并修改T的右指针指向
	return LRotate(T);               // 对T树进行左旋处理
}

四、平衡二叉树基本操作

1、查找

（1）查找定值

对于要查找的数据 data，从根结点出发，每次选择左子树或者右子树进行查找， n 个结点的树高最多为，所以查找的时间复杂度为 O() ，总共四种情况依次进行判断：

1）若为空树，直接返回 false；

2） data 小于 树根结点的数据域，说明 data 对应的结点不在根结点，也不在右子树上，则递归返回左子树的 查找 结果；

3） data 大于 树根结点的数据域，说明 data 对应的结点不在根结点，也不在左子树上，则递归返回右子树的 查找 结果；

4） data 等于 树根结点的数据域，则直接返回 true ；

bool AVLFind(TreeNode* T, int data) {
	if (T == nullptr) {
		return false;                        // 空树
	}
	if (data < T->val) {
		return AVLFind(T->left, data);       // data T->val) {
		return AVLFind(T->right, data);      //  data>val，递归查找右子树
	}
	return true;                             //  data=val
}

（2）查找最小值结点

迭代找到树的最左结点即可。

//找最小值结点
TreeNode* AVLGetMin(TreeNode* T) {
	while (T && T->left)   
		T = T->left;       
	return T;              
}

（3）查找最大值

迭代找到树的最右结点即可。

//找最大值结点
TreeNode* AVLGetMax(TreeNode* T) {
	while (T && T->right)  
		T = T->right;      
	return T;              
}

2、平衡

每次当我们对树的结点进行插入或者删除的时候，都有可能打破树的平衡性，这时候就需要一些旋转操作来使树重新恢复平衡。 究竟是进行左旋，右旋，还是双旋，就要通过平衡因子来判断了。

令根结点为 T ，左子树的根结点为 L ，右子树的根结点为 R ， 代表根结点的平衡因子，代表左子树根的平衡因子， 代表右子树根的平衡因子。总共分为以下四种情况：

1）   > 1 ，  > 0 ，则为 LL 型，需要进行一次右旋；

2）   > 1 ，  ≤ 0 ，则为 LR 型，需要进行一次双旋；

3）   < −1 ，  > 0 ，则为 RL 型，需要进行一次双旋；

4）   < −1 ，  ≤ 0 ，则为 RR 型，需要进行一次左旋

 平衡源码

//平衡选转
TreeNode* AVLBalance(TreeNode* T) {
	int bf = AVLGetBalanceFactor(T);

	if (bf > 1) {
		if (AVLGetBalanceFactor(T->left) > 0)
			T = AVLTreeLL(T);                 // LL型，右旋一次
		else
			T = AVLTreeLR(T);                 // LR型，左旋+右旋 
	}
	if (bf < -1) {
		if (AVLGetBalanceFactor(T->right) > 0)
			T = AVLTreeRL(T);                 // RL型，右旋+左旋 
		else
			T = AVLTreeRR(T);                 // RR型，左旋一次
	}
	AVLCalcHeight(T);                         // 重新计算根结点高度，因为之前旋转时并未完成相关操作
	return T;                                 
}

3、插入

对于要插入的数据 data ，从根结点出发，分情况依次判断：

1）若为空树，则创建一个值为 data 的结点并且返回；

2） data 的值 等于 树根结点的值，无须执行插入，直接返回根结点；

3） data 的值 小于 树根结点的值，那么插入位置一定在 左子树，递归执行插入左子树的过程，并且返回插入结果作为新的左子树；

4） data 的值 大于 树根结点的值，那么插入位置一定在 右子树，递归执行插入右子树的过程，并且返回插入结果作为新的右子树；

最后，在3或4情况执行完成后，需要对树执行 平衡 操作。

插入源码

TreeNode* AVLInsert(TreeNode* T, int data) {
	if (T == nullptr) {
		T = new TreeNode(data);               // 空树，创建val=data的结点
		return T;
	}

	if (data == T->val) {
		return T;                              // data已经存在
	}
	else if (data < T->val) {
		T->left = AVLInsert(T->left, data);    // 递归查找左子树适合位置，插入 
	}
	else {
		T->right = AVLInsert(T->right, data);  // 递归查找右子树适合位置，插入 
	}
	return AVLBalance(T);                      // 重新平衡 
}

4、删除

（1）删除根结点

对一棵平衡二叉树，删除它的根结点，需要保证它还是一棵二叉平衡树，则有如下四种情况：

1）空树，无须执行删除，直接返回空；

2）只有左子树时，将根结点空间释放后，返回左子树；

3）只有右子树时，将根结点空间释放后，返回右子树；

4）当左右子树都有时，根据左右子树的平衡性分情况讨论：如果左子树更高，则从左子树选择最大值替换根结点，并且递归删除左子树对应结点；右子树更高，则从右子树选择最小值替换根结点，并且递归删除右子树对应结点；

5）最后，重新计算所有树高，并且返回根结点；

//删除根结点
TreeNode* AVLRemoveRoot(TreeNode* T) {
	TreeNode* delNode = nullptr;
	TreeNode* retNode = nullptr;
	if (T == nullptr) {
		return nullptr;                 // 空树，直接返回 
	}

	if (T->right == nullptr) {    // 只有左子树（包含单节点情况），释放根结点空间后，返回左子树根结点
		retNode = T->left;
		delete T;
	}
	else if (T->left == nullptr) {    // 只有右子树，释放根结点空间后，返回右子树根结点 
		retNode = T->right;
		delete T;
	}
	else {								// 左右子树都存在 
		if (AVLGetHeight(T->left) > AVLGetHeight(T->right)) {  // 左子树高于右子树
			retNode = T;
			//获取左子树最大值结点,并以它的值作为根结点的新值
			TreeNode* cur = T->left;
			TreeNode* pcur = T;
			while (cur->right)
			{
				pcur = cur;
				cur = cur->right;
			}
			delNode = cur;
			retNode->val = cur->val;

			if (pcur->right == cur) {//左子树的最大值在左子树的右子树上
				pcur->right = cur->left;
			}
			else {//左子树的最大值为左子树的根
				pcur->left = cur->left;
			}
			delete delNode;

			
			retNode = AVLBalance(T);
			AVLCalcAllHeight(retNode);
			
		}
		else {   // 右子树高于左子树
			retNode = T;
			//获取右子树最小值结点,并以它的值作为根结点的新值
			TreeNode* cur = T->right;
			TreeNode* pcur = T;
			while (cur->left)
			{
				pcur = cur;
				cur = cur->left;
			}
			delNode = cur;
			retNode->val = cur->val;

			if (pcur->left == cur) {//右子树的最小值在右子树的左子树上
				pcur->left = cur->right;
			}
			else {//右子树的最小值为右子树的根
				pcur->right = cur->right;
			}
			delete delNode;

			retNode = AVLBalance(T);
			AVLCalcAllHeight(retNode);
		}
	}
	return retNode;
}

（2）删除指定结点

删除值为 data 的结点的过程，从根结点出发，总共四种情况依次判断：

1）空树，不存在结点，直接返回空 ；

2） data 的值 等于 树根结点的值，则调用 删除根结点 的接口，这个过程下文会详细介绍；

3） data 的值 小于 树根结点的值，则需要删除的结点一定不在右子树上，递归调用删除左子树的对应结点，并且将删除结点返回的子树作为新的左子树；

4） data 的值 大于 树根结点的值，则需要删除的结点一定不在左子树上，递归调用删除右子树的对应结点，并且将删除结点返回的子树作为新的右子树；

5）最后，对于 3） 和 4） 这两步，需要对树执行 平衡 操作。

TreeNode* AVLRemove(TreeNode* root,int val)
{
	if (nullptr == root) {
		return nullptr;
	}
	if (val == root->val) {
		return AVLRemoveRoot(root);
	}
	else if (val < root->val) {
		root->left = AVLRemove(root->left, val);
	}
	else if (val > root->val) {
		root->right = AVLRemove(root->right, val);
	}
	root = AVLBalance(root);
	AVLCalcAllHeight(root);
	return root;
}

五、平衡二叉树的缺点

由于AVL树必须保证左右子树平衡，Max(最大树高-最小树高) <= 1，所以在插入的时候很容易出现不平衡的情况，一旦这样，就需要进行旋转以求达到平衡。

正是由于这种严格的平衡条件，导致AVL需要花大量时间在调整上，故AVL树一般使用场景在于查询场景， 而不是 增加、删除频繁的场景。