【数据结构】二叉树的链式实现
树是数据结构中非常重要的一种,在计算机的各方个面都有他的身影
此篇文章主要介绍二叉树的基本操作
目录
- 二叉树的定义:
- 二叉树的创建:
- 二叉树的遍历:
-
- 前序遍历:
- 中序遍历:
- 后序遍历:
- 二叉树节点个数:
- 二叉树叶子结点个数:
- 二叉树第k层节点个数:
- 二叉树查找值为x的节点:
- 二叉树的销毁:
二叉树的定义:
这里我们使用char,因为二叉树的创建我们会使用递归创建,需要传入一个字符串进行操作
typedef char BTDataType;
typedef struct BinaryTreeNode
{
BTDataType data;
struct BinaryTreeNode* left;
struct BinaryTreeNode* right;
}BTNode;
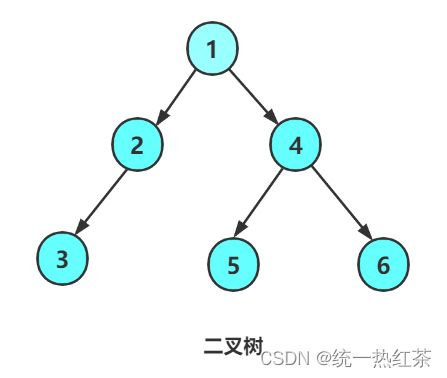
二叉树的创建:
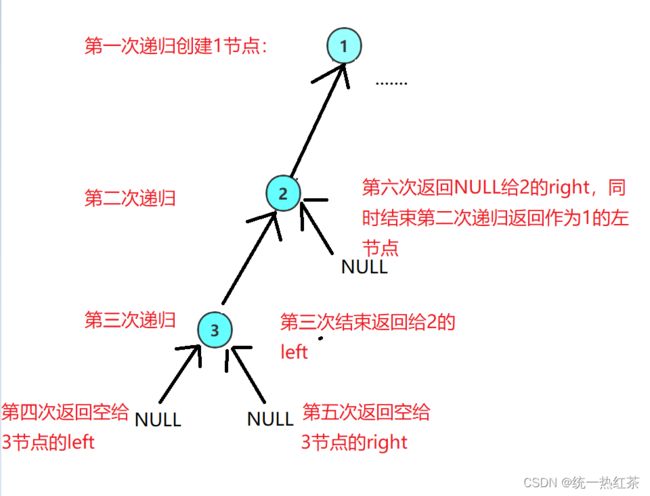
我们通过前序遍历的数组"123###45##6##"构建二叉树
这里讲一下我使用递归做题时的一些做题感受方法:
- 首先写出递归的结束条件,这是每个递归都不可以缺少的
- 利用分治的思想(将一个问题分成几个相同的子问题)
- 把你的递归想象是可以完成你既定的任务
- 写出你调用这个递归需要本次进行的工作
- 完成后可以画出一个递归展开图进行验证
接下来我会仔细带着大家仔细领悟,熟能生巧,同学们一定不要气馁
先解释一下这个函数传参的意义:
BTNode* BinaryTreeCreate(BTDataType* a, int* pi)
a就是我们传参的字符数组
pi是我们字符数组的下标,为什么需要下标的地址呢,因为形参的改变不会影响实参
BTNode* BinaryTreeCreate(BTDataType* a, int* pi)
{
if (a[*pi] == '#')
{
(*pi)++;
return NULL;
}
BTNode* root = (BTNode*)malloc(sizeof(BTNode));
if (root == NULL)
{
perror("malloc fail");
return;
}
root->data = a[(*pi)++];
root->left = BinaryTreeCreate(a, pi);
root->right = BinaryTreeCreate(a, pi);
return root;
}
- 做递归时截止条件是必不可少的,我们选择使用叶子节点是否为空作为判断标准。
- 我们将这个问题从创建一个完整二叉树分成先创建一个节点并连接他的左右节点的问题·
- 我们现在需要完成此时函数需要完成的任务,此次函数的目的是创造一个二叉树,我们需要对
root->val进行赋值,再将root的左右子树进行连接 - 此时观察整个函数,我们发现我们已经生成了一个
root节点,也进行了赋值,root的左右节点也都分别使用BinaryTreeCreate(a, n, pi)这个函数进行连接,我们已经把此函数当做可以完成既定任务的,不需要过多纠结,此时我们在加一个返回值root,就完成了此次函数的创建
二叉树的递归图:
二叉树的遍历:
前序遍历:
有了以上的思路就可以很简单的实现了
void BinaryTreePrevOrder(BTNode* root)
{
if (root == NULL)
{
printf("N ");
return;
}
printf("%c ", root->data);
BinaryTreePrevOrder(root->left);
BinaryTreePrevOrder(root->right);
}
代码也很简洁
- NULL结束条件
- 分治:前序是根左右的遍历,故我们先遍历根,在遍历左子树右子树
- 没有返回值,不需要return
就像下图这样,将这个程序当成可以完成任务的函数。
printf("%c ", root->data);//进行本次的任务
BinaryTreePrevOrder(root->left);//遍历左子树
BinaryTreePrevOrder(root->right);//遍历左子树
中序遍历:
与前序遍历一致
void BinaryTreePrevOrder(BTNode* root)
{
if (root == NULL)
{
printf("N ");
return;
}
BinaryTreePrevOrder(root->left);
printf("%c ", root->data);
BinaryTreePrevOrder(root->right);
}
后序遍历:
void BinaryTreePrevOrder(BTNode* root)
{
if (root == NULL)
{
printf("N ");
return;
}
BinaryTreePrevOrder(root->left);
BinaryTreePrevOrder(root->right);
printf("%c ", root->data);
}
二叉树节点个数:
int BinaryTreeSize(BTNode* root)
{
if (root == NULL)
{
return 0;
}
return BinaryTreeSize(root->left) +
BinaryTreeSize(root->right) + 1;
}
- 结束条件为
NULL - 分治:将这个问题当成当前节点+左子树节点与右子树节点
- return 当前节点+左子树节点与右子树节点
二叉树叶子结点个数:
int BinaryTreeLeafSize(BTNode* root)
{
if (root == NULL)
{
return 0;
}
if (root->left == NULL && root->right == NULL)
{
return 1;
}
return BinaryTreeLeafSize(root->left) +
BinaryTreeLeafSize(root->right);
}
- 结束条件有两个(因为当前节点不为空节点才能是叶子节点),为空或为叶子节点
- 分治:将问题变为左子树的叶子节点与右子树的叶子结点
- 返回总结点个数
二叉树第k层节点个数:
int BinaryTreeLevelKSize(BTNode* root, int k)
{
if (root == NULL)
{
return 0;
}
if (k == 1)
{
return 1;
}
return BinaryTreeLevelKSize(root->left, k - 1) +
BinaryTreeLevelKSize(root->right, k - 1);
}
1.结束条件有两个,当为NULL或为目标层数时为结束
2. 分治:这个的分治并不像上边的简单了,我们需要root的第k层转化为root->左子树的k-1层与root->right的k-1层,将K也作为函数传参,每次减1
3. 返回第k层节点个数
二叉树查找值为x的节点:
我们先来看这样一段代码,相信有许多小伙伴在遇到
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{
if (root == NULL)
{
return NULL;
}
if (root->data == x)
{
return root;
}
BinaryTreeFind(root->left, x);
BinaryTreeFind(root->right, x);
return NULL;
}
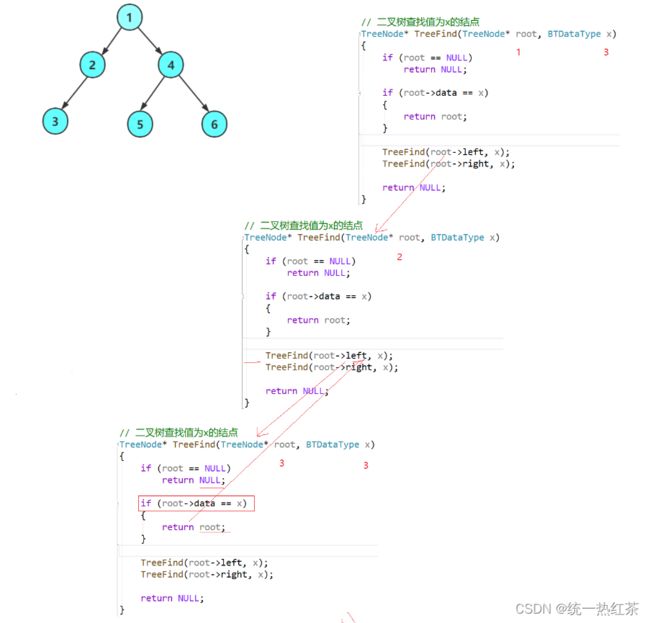
乍一看好像没什么问题,不就是前序遍历嘛,
不然,实则我们并没有记录找到的地址,像下图一样
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{
if (root == NULL)
{
return NULL;
}
if (root->data == x)
{
return root;
}
BTNode* ret1 = BinaryTreeFind(root->left, x);
if (ret1)
{
return ret1;
}
BTNode* ret2 = BinaryTreeFind(root->right, x);
if (ret2)
{
return ret2;
}
return NULL;
}
- 结束为
NULL或目标值 - 分治:当前节点+左子树+右子树进行前序遍历
- 记录
ret值并返回
二叉树的销毁:
使用后序遍历,因为前序与中序需要记录当前被销毁的左右节点地址
void BinaryTreeDestory(BTNode* root)
{
if (root == NULL)
{
return;
}
BinaryTreeDestory(root->left);
BinaryTreeDestory(root->right);
free(root);
}
持续更新中…