通过标识提升冒泡排序
在维基上看到,可以通过添加标识来分辨剩余的数是否已经有序来减少比较次数。感觉很有意思,可以试试。
实现如下:
1 public static void BubbleSortImprovedWithFlag(IList data)
2 {
3 bool flag;
4 for (int i = data.Count - 1; i > 0; i--)
5 {
6 flag = true;
7 for (int j = 0; j < i; j++)
8 {
9 if (data[j] > data[j + 1])
10 {
11 Swap(data, j, j + 1);
12 flag = false;
13 }
14 }
15 if (flag) break;
16 }
17 }
过程解析:发现某轮冒泡没有任何数进行交换(即已经有序),就跳出排序。
我起初也以为这个方法是应该有不错效果的,可是实际测试结果并不如想的那样。和未优化耗费时间一样(对于随机数列)。
由果推因,那么应该是冒泡排序对于随机数列,当剩余数列有序的时候,也没几个数要排列了!?
不过如果已经是有序数列或者部分有序的话,这个冒泡方法将会提升很大速度。
鸡尾酒排序(来回排序)
对冒泡排序进行更大的优化
冒泡排序只是单向冒泡,而鸡尾酒来回反复双向冒泡。
原理:自左向右将大数冒到末尾,然后将剩余数列再自右向左将小数冒到开头,如此循环往复。维基入口
实现如下:
1 public static void BubbleCocktailSort(IList data)
2 {
3 bool flag;
4 int m = 0, n = 0;
5 for (int i = data.Count - 1; i > 0; i--)
6 {
7 flag = true;
8 if (i % 2 == 0)
9 {
10 for (int j = n; j < data.Count - 1 - m; j++)
11 {
12 if (data[j] > data[j + 1])
13 {
14 Swap(data, j, j + 1);
15 flag = false;
16 }
17 }
18 if (flag) break;
19 m++;
20 }
21 else
22 {
23 for (int k = data.Count - 1 - m; k > n; k--)
24 {
25 if (data[k] < data[k - 1])
26 {
27 Swap(data, k, k - 1);
28 flag = false;
29 }
30 }
31 if (flag) break;
32 n++;
33 }
34 }
35 }
过程解析:分析第i轮冒泡,i是偶数则将剩余数列最大值向右冒泡至末尾,是奇数则将剩余数列最小值
向左冒泡至开头。对于剩余数列,n为始,data.Count-1-m为末。
来回冒泡比单向冒泡:对于随机数列,更容易得到有序的剩余数列。因此这里使用标识将会提升的更加明显。
插入排序
插入排序是一种对于有序数列高效的排序。非常聪明的排序。只是对于随机数列,效率一般,交换的频率高。
原理:通过构建有序数列,将未排序的数从后向前比较,找到合适位置并插入。维基入口
第一个数当作有序数列。
实现如下:
1 public static void InsertSort(IList data)
2 {
3 int temp;
4 for (int i = 1; i < data.Count; i++)
5 {
6 temp = data[i];
7 for (int j = i - 1; j >= 0; j--)
8 {
9 if (data[j] > temp)
10 {
11 data[j + 1] = data[j];
12 if (j == 0)
13 {
14 data[0] = temp;
15 break;
16 }
17 }
18 else
19 {
20 data[j + 1] = temp;
21 break;
22 }
23 }
24 }
25 }
过程解析:将要排序的数(索引为i)存储起来,向前查找合适位置j+1,将i-1到j+1的元素依次向后
移动一位,空出j+1,然后将之前存储的值放在这个位置。
这个方法写的不如维基上的简洁清晰,由于合适位置是j+1所以多出了对j==0的判断,但实际效率影响无差别。
建议比照维基和我写的排序,自行选择。
二分查找法优化插入排序
插入排序主要工作是在有序的数列中对要排序的数查找合适的位置,而查找里面经典的二分查找法正可以适用。
原理:通过二分查找法的方式找到一个位置索引。当要排序的数插入这个位置时,大于前一个数,小于后一个数。
实现如下:
1 public static void InsertSortImprovedWithBinarySearch(IList data)
2 {
3 int temp;
4 int tempIndex;
5 for (int i = 1; i < data.Count; i++)
6 {
7 temp = data[i];
8 tempIndex = BinarySearchForInsertSort(data, 0, i, i);
9 for (int j = i - 1; j >= tempIndex; j--)
10 {
11 data[j + 1] = data[j];
12 }
13 data[tempIndex] = temp;
14 }
15 }
16
17 public static int BinarySearchForInsertSort(IList data, int low, int high, int key)
18 {
19 if (low >= data.Count - 1)
20 return data.Count - 1;
21 if (high <= 0)
22 return 0;
23 int mid = (low + high) / 2;
24 if (mid == key) return mid;
25 if (data[key] > data[mid])
26 {
27 if (data[key] < data[mid + 1])
28 return mid + 1;
29 return BinarySearchForInsertSort(data, mid + 1, high, key);
30 }
31 else // data[key] <= data[mid]
32 {
33 if (mid - 1 < 0) return 0;
34 if (data[key] > data[mid - 1])
35 return mid;
36 return BinarySearchForInsertSort(data, low, mid - 1, key);
37 }
38 }
过程解析:需要注意的是二分查找方法实现中high-low==1的时候mid==low,所以需要33行
mid-1<0即mid==0的判断,否则下行会索引越界。
快速排序
快速排序是一种有效比较较多的高效排序。它包含了“分而治之”以及“哨兵”的思想。
原理:从数列中挑选一个数作为“哨兵”,使比它小的放在它的左侧,比它大的放在它的右侧。将要排序是数列递归地分割到
最小数列,每次都让分割出的数列符合“哨兵”的规则,自然就将数列变得有序。 维基入口
实现如下:
1 public static void QuickSortStrict(IList data)
2 {
3 QuickSortStrict(data, 0, data.Count - 1);
4 }
5
6 public static void QuickSortStrict(IList data, int low, int high)
7 {
8 if (low >= high) return;
9 int temp = data[low];
10 int i = low + 1, j = high;
11 while (true)
12 {
13 while (data[j] > temp) j--;
14 while (data[i] < temp && i < j) i++;
15 if (i >= j) break;
16 Swap(data, i, j);
17 i++; j--;
18 }
19 if (j != low)
20 Swap(data, low, j);
21 QuickSortStrict(data, j + 1, high);
22 QuickSortStrict(data, low, j - 1);
23 }
过程解析:取的哨兵是数列的第一个值,然后从第二个和末尾同时查找,左侧要显示的是小于哨兵的值,
所以要找到不小于的i,右侧要显示的是大于哨兵的值,所以要找到不大于的j。将找到的i和j的数交换,
这样可以减少交换次数。i>=j时,数列全部查找了一遍,而不符合条件j必然是在小的那一边,而哨兵
是第一个数,位置本应是小于自己的数。所以将哨兵与j交换,使符合“哨兵”的规则。
这个版本的缺点在于如果是有序数列排序的话,递归次数会很可怕的。
另一个版本
这是维基上的一个C#版本,我觉得很有意思。这个版本并没有严格符合“哨兵”的规则。但却将“分而治之”
以及“哨兵”思想融入其中,代码简洁。
实现如下:
1 public static void QuickSortRelax(IList data)
2 {
3 QuickSortRelax(data, 0, data.Count - 1);
4 }
5
6 public static void QuickSortRelax(IList data, int low, int high)
7 {
8 if (low >= high) return;
9 int temp = data[(low + high) / 2];
10 int i = low - 1, j = high + 1;
11 while (true)
12 {
13 while (data[++i] < temp) ;
14 while (data[--j] > temp) ;
15 if (i >= j) break;
16 Swap(data, i, j);
17 }
18 QuickSortRelax(data, j + 1, high);
19 QuickSortRelax(data, low, i - 1);
20 }
过程解析:取的哨兵是数列中间的数。将数列分成两波,左侧小于等于哨兵,右侧大于等于哨兵。
也就是说,哨兵不一定处于两波数的中间。虽然哨兵不在中间,但不妨碍“哨兵”的思想的实现。所以
这个实现也可以达到快速排序的效果。但却造成了每次递归完成,要排序的数列数总和没有减少(除非i==j)。
针对这个版本的缺点,我进行了优化
实现如下:
1 public static void QuickSortRelaxImproved(IList data)
2 {
3 QuickSortRelaxImproved(data, 0, data.Count - 1);
4 }
5
6 public static void QuickSortRelaxImproved(IList data, int low, int high)
7 {
8 if (low >= high) return;
9 int temp = data[(low + high) / 2];
10 int i = low - 1, j = high + 1;
11 int index = (low + high) / 2;
12 while (true)
13 {
14 while (data[++i] < temp) ;
15 while (data[--j] > temp) ;
16 if (i >= j) break;
17 Swap(data, i, j);
18 if (i == index) index = j;
19 else if (j == index) index = i;
20 }
21 if (j == i)
22 {
23 QuickSortRelaxImproved(data, j + 1, high);
24 QuickSortRelaxImproved(data, low, i - 1);
25 }
26 else //i-j==1
27 {
28 if (index >= i)
29 {
30 if (index != i)
31 Swap(data, index, i);
32 QuickSortRelaxImproved(data, i + 1, high);
33 QuickSortRelaxImproved(data, low, i - 1);
34 }
35 else //index < i
36 {
37 if (index != j)
38 Swap(data, index, j);
39 QuickSortRelaxImproved(data, j + 1, high);
40 QuickSortRelaxImproved(data, low, j - 1);
41 }
42 }
43 }
过程解析:定义了一个变量Index,来跟踪哨兵的位置。发现哨兵最后在小于自己的那堆,
那就与j交换,否则与i交换。达到每次递归都能减少要排序的数列数总和的目的。
归并排序
归并排序也是采用“分而治之”的方式。刚发现分治法是一种算法范式,我还一直以为是一种需要意会的思想呢。
不好意思了,孤陋寡闻了,哈哈!
原理:将两个有序的数列,通过比较,合并为一个有序数列。 维基入口
为方便理解,此处实现用了List的一些方法,随后有IList版本。
实现如下:
1 public static List MergeSortOnlyList(List data, int low, int high)
2 {
3 if (low == high)
4 return new List { data[low] };
5 List mergeData = new List();
6 int mid = (low + high) / 2;
7 List leftData = MergeSortOnlyList(data, low, mid);
8 List rightData = MergeSortOnlyList(data, mid + 1, high);
9 int i = 0, j = 0;
10 while (true)
11 {
12 if (leftData[i] < rightData[j])
13 {
14 mergeData.Add(leftData[i]);
15 if (++i == leftData.Count)
16 {
17 mergeData.AddRange(rightData.GetRange(j, rightData.Count - j));
18 break;
19 }
20 }
21 else
22 {
23 mergeData.Add(rightData[j]);
24 if (++j == rightData.Count)
25 {
26 mergeData.AddRange(leftData.GetRange(i, leftData.Count - i));
27 break;
28 }
29 }
30 }
31 return mergeData;
32 }
33
34 public static List MergeSortOnlyList(List data)
35 {
36 data = MergeSortOnlyList(data, 0, data.Count - 1); //不会改变外部引用 参照C#参数传递
37 return data;
38 }
过程解析:将数列分为两部分,分别得到两部分数列的有序版本,然后逐个比较,将比较出的小数逐个放进
新的空数列中。当一个数列放完后,将另一个数列剩余数全部放进去。
IList版本
实现如下:

1 public static IList MergeSort(IList data)
2 {
3 data = MergeSort(data, 0, data.Count - 1);
4 return data;
5 }
6
7 public static IList MergeSort(IList data, int low, int high)
8 {
9 int length = high - low + 1;
10 IList mergeData = NewInstance(data, length);
11 if (low == high)
12 {
13 mergeData[0] = data[low];
14 return mergeData;
15 }
16 int mid = (low + high) / 2;
17 IList leftData = MergeSort(data, low, mid);
18 IList rightData = MergeSort(data, mid + 1, high);
19 int i = 0, j = 0;
20 while (true)
21 {
22 if (leftData[i] < rightData[j])
23 {
24 mergeData[i + j] = leftData[i++]; //不能使用Add,Array Length不可变
25 if (i == leftData.Count)
26 {
27 int rightLeft = rightData.Count - j;
28 for (int m = 0; m < rightLeft; m++)
29 {
30 mergeData[i + j] = rightData[j++];
31 }
32 break;
33 }
34 }
35 else
36 {
37 mergeData[i + j] = rightData[j++];
38 if (j == rightData.Count)
39 {
40 int leftleft = leftData.Count - i;
41 for (int n = 0; n < leftleft; n++)
42 {
43 mergeData[i + j] = leftData[i++];
44 }
45 break;
46 }
47 }
48 }
49 return mergeData;
50
51 }

过程原理与上个一样,此处就不赘述了。
堆排序
堆排序是根据堆这种数据结构设计的一种算法。堆的特性:父节点的值总是小于(或大于)它的子节点。近似二叉树。
原理:将数列构建为最大堆数列(即父节点总是最大值),将最大值(即根节点)交换到数列末尾。这样要排序的数列数总和减少,
同时根节点不再是最大值,调整最大堆数列。如此重复,最后得到有序数列。 维基入口 有趣的演示
实现准备:如何将数列构造为堆——父节点i的左子节点为2i+1,右子节点为2i+2。节点i的父节点为floor((i-1)/2)。
实现如下(这个实现判断和临时变量使用太多,导致效率低,评论中@小城故事提出了更好的实现):

1 public static void HeapSort(IList data)
2 {
3 BuildMaxHeapify(data);
4 int j = data.Count;
5 for (int i = 0; i < j; )
6 {
7 Swap(data, i, --j);
8 if (j - 2 < 0) //只剩下1个数 j代表余下要排列的数的个数
9 break;
10 int k = 0;
11 while (true)
12 {
13 if (k > (j - 2) / 2) break; //即:k > ((j-1)-1)/2 超出最后一个父节点的位置
14 else
15 {
16 int temp = k;
17 k = ReSortMaxBranch(data, k, 2 * k + 1, 2 * k + 2, j - 1);
18 if (temp == k) break;
19 }
20 }
21 }
22 }
23
24 public static void BuildMaxHeapify(IList data)
25 {
26 for (int i = data.Count / 2 - 1; i >= 0; i--) //(data.Count-1)-1)/2为数列最大父节点索引
27 {
28 int temp = i;
29 temp = ReSortMaxBranch(data, i, 2 * i + 1, 2 * i + 2, data.Count - 1);
30 if (temp != i)
31 {
32 int k = i;
33 while (k != temp && temp <= data.Count / 2 - 1)
34 {
35 k = temp;
36 temp = ReSortMaxBranch(data, temp, 2 * temp + 1, 2 * temp + 2, data.Count - 1);
37 }
38 }
39 }
40 }
41
42 public static int ReSortMaxBranch(IList data, int maxIndex, int left, int right, int lastIndex)
43 {
44 int temp;
45 if (right > lastIndex) //父节点只有一个子节点
46 temp = left;
47 else
48 {
49 if (data[left] > data[right])
50 temp = left;
51 else temp = right;
52 }
53
54 if (data[maxIndex] < data[temp])
55 Swap(data, maxIndex, temp);
56 else temp = maxIndex;
57 return temp;
58 }

过程解析:BuildMaxHeapify为排序前构建的最大堆数列方法,主要内容为从最后一个父节点开始往前将每个三角组合
(即父节点与它的两个子节点)符合父节点值最大的规则。ReSortMaxBranch为将三角调整为父节点值最大,
并返回该值之前的索引,用来判断是否进行了交换,以及原来的父节点值交换到了什么位置。在HeapSort里首先
构建了最大堆数列,然后将根节点交换到末尾,根节点不是最大值了,在while语句中对最大堆数列进行调整。
插曲:自从看了Martin Fowler大师《重构》第三版,我发现我更不喜欢写注释了。每次都想着尽量让方法的名字更贴切,
即使会造成方法的名字很长很丑。这算不算曲解了大师的意思啊!?上面的代码注释都是写博客的时候现加的(源代码很干净的。汗!)。
希尔排序
希尔排序是插入排序的一种更高效的改进版本。
在前面介绍的插入排序,我们知道1.它对有序数列排序的效率是非常高的 2.要排序的数向前移动是一步步进行的导致插入排序效率低。
希尔排序正是利用第一点,改善第二点,达到更理想的效果。
原理:通过奇妙的步长,插入排序间隔步长的元素,随后逐渐缩短步长至1,实现数列的插入排序。 维基入口
疑问:可以想象到排序间隔步长的数,会逐渐让数列变得有序,提升最后步长为1时标准插入排序的效率。在维基上看到这么
一句话“可能希尔排序最重要的地方在于当用较小步长排序后,以前用的较大步长仍然是有序的”注意用词是‘可能’。我的疑问是
这是个正确的命题吗?如何证明呢?看维基上也是由果推因,说是如果不是这样,就不会排序那么快了。可这我感觉还是太牵强了,
哪位大哥发现相关资料,希望能分享出来,不胜感激。
实现如下:
1 public static void ShellSort(IList data)
2 {
3 int temp;
4 for (int gap = data.Count / 2; gap > 0; gap /= 2)
5 {
6 for (int i = gap; i < data.Count; i += gap)
7 {
8 temp = data[i];
9 for (int j = i - gap; j >= 0; j -= gap)
10 {
11 if (data[j] > temp)
12 {
13 data[j + gap] = data[j];
14 if (j == 0)
15 {
16 data[j] = temp;
17 break;
18 }
19 }
20 else
21 {
22 data[j + gap] = temp;
23 break;
24 }
25 }
26 }
27 }
28 }
过程解析:采用的步长是N/2,每次取半,直至1。循环内部就是标准的插入排序。
——————
修正:修正后希尔排序才是真正牛叉的希尔啊!感谢@390218462的提出
1 public static void ShellSortCorrect(IList data)
2 {
3 int temp;
4 for (int gap = data.Count / 2; gap > 0; gap /= 2)
5 {
6 for (int i = gap; i < data.Count; i++) // i+ = gap 改为了 i++
7 {
8 temp = data[i];
9 for (int j = i - gap; j >= 0; j -= gap)
10 {
11 if (data[j] > temp)
12 {
13 data[j + gap] = data[j];
14 if (j == 0)
15 {
16 data[j] = temp;
17 break;
18 }
19 }
20 else
21 {
22 data[j + gap] = temp;
23 break;
24 }
25 }
26 }
27 }
28 }


——————
这里实现的貌似是最差的希尔排序。主要源于步长的选择。维基上有各种牛叉的“凌波微步”,极限在哪里,
喜欢挑战的同学可以去学习学习。看维基排序算法里六种排序的测试,希尔最快,比快速排序还快!!我没实现啊!
只是对于神奇的步长更充满了敬畏。
基数排序
基数排序是一种非比较型整数排序。
“非比较型”是什么意思呢?因为它内部使用的是桶排序,而桶排序是非比较型排序。
这里就要说说桶排序了。一个非常有意思的排序。
桶排序
原理:取一定数量(数列中的最大值)的编好序号的桶,将数列每个数放进编号为它的桶里,然后将不是空的桶依次倒出来,
就组成有序数列了。 维基入口
好吧!聪明的人一眼就看出桶排序的破绽了。假设只有两个数1,10000,岂不是要一万个桶!?这确实是个问题啊!我也
没想出解决办法。我起初也以为桶排序就是一个通过牺牲空间来换取时间的排序算法,它不需要比较,所以是非比较型算法。
但看了有趣的演示的桶排序后,发现世界之大,你没有解决,不代表别人没解决,睿智的人总是很多。
1,9999的桶排序实现:new Int[2];总共有两个数,得出最大数9999的位数4,取10的4次幂即10000作为分母,
要排序的数(1或9999)作为分子,并乘以数列总数2,即1*2/10000,9999*2/10000得到各自的位置0,1,完成排序。
如果是1,10000进行排序的话,上面的做法就需要稍微加一些处理——发现最大数是10的n次幂,就将它作为分母,并
放在数列末尾就好了。
如果是9999,10000进行排序的话,那就需要二维数组了,两个都在位置1,位置0没数。这个时候就需要在放
入每个位置时采用其它排序(比如插入排序)办法对这个位置的多个数排序了。
为基数排序做个过渡,我这里实现了一个个位数桶排序
涉及到了当重复的数出现的处理。
实现如下:
1 public static void BucketSortOnlyUnitDigit(IList data)
2 {
3 int[] indexCounter = new int[10];
4 for (int i = 0; i < data.Count; i++)
5 {
6 indexCounter[data[i]]++;
7 }
8 int[] indexBegin = new int[10];
9 for (int i = 1; i < 10; i++)
10 {
11 indexBegin[i] = indexBegin[i-1]+ indexCounter[i-1];
15 }
16 IList tempList = NewInstance(data, data.Count);
17 for (int i = 0; i < data.Count; i++)
18 {
19 int number = data[i];
20 tempList[indexBegin[number]++] = data[i];
21 }
22 data = tempList;
23 }
过程解析:indexCounter进行对每个数出现的频率的统计。indexBegin存储每个数的起始索引。
比如 1 1 2,indexCounter统计到0个0,2个1,1个2。indexBegin计算出0,1,2的起始索引分别为
0,0,2。当1个1已取出排序,那索引将+1,变为0,1,2。这样就通过提前给重复的数空出位置,解决了
重复的数出现的问题。当然,你也可以考虑用二维数组来解决重复。
下面继续基数排序。
基数排序原理:将整数按位数切割成不同的数字,然后按每个位数分别比较。
取得最大数的位数,从低位开始,每个位上进行桶排序。
实现如下:
1 public static IList RadixSort(IList data)
2 {
3 int max = data[0];
4 for (int i = 1; i < data.Count; i++)
5 {
6 if (data[i] > max)
7 max = data[i];
8 }
9 int digit = 1;
10 while (max / 10 != 0)
11 {
12 digit++;
13 max /= 10;
14 }
15 for (int i = 0; i < digit; i++)
16 {
17 int[] indexCounter = new int[10];
18 IList tempList = NewInstance(data, data.Count);
19 for (int j = 0; j < data.Count; j++)
20 {
21 int number = (data[j] % Convert.ToInt32(Math.Pow(10, i + 1))) / Convert.ToInt32(Math.Pow(10, i)); //得出i+1位上的数
22 indexCounter[number]++;
23 }
24 int[] indexBegin = new int[10];
25 for (int k = 1; k < 10; k++)
26 {
27 indexBegin[k] = indexBegin[k - 1] + indexCounter[k - 1];
28 }
29 for (int k = 0; k < data.Count; k++)
30 {
31 int number = (data[k] % Convert.ToInt32(Math.Pow(10, i + 1))) / Convert.ToInt32(Math.Pow(10, i));
32 tempList[indexBegin[number]++] = data[k];
33 }
34 data = tempList;
35 }
36 return data;
37 }
过程解析:得出最大数的位数,从低位开始桶排序。我写的这个实现代码并不简洁,但逻辑更清晰。
后面测试的时候我们就会发现,按理来说这个实现也还行吧! 但并不如想象的那么快!
循环的次数太多?(统计频率n次+9次计算+n次放到新的数组)*位数。
创建的新实例太多?(new int[10]两次+NewInstance is反射判断创建实例+new int[n])*位数
测试比较
添加随机数组,数组有序校验,微软Linq排序
代码如下:
1 public static int[] RandomSet(int length, int max)
2 {
3 int[] result = new int[length];
4 Random rand = new Random();
5 for (int i = 0; i < result.Length; i++)
6 {
7 result[i] = rand.Next(max);
8 }
9 return result;
10 }
11
12 public static bool IsAscOrdered(IList data)
13 {
14 bool flag = true;
15 for (int i = 0; i < data.Count - 1; i++)
16 {
17 if (data[i] > data[i + 1])
18 flag = false;
19 }
20 return flag;
21 }
22
23 public static void TestMicrosoft(IList data)
24 {
25 Stopwatch stopwatch = new Stopwatch();
26 stopwatch.Start();
27 List result = data.OrderBy(a => a).ToList();
28 stopwatch.Stop();
29 string methodName = "TestMicrosoft";
30 int length = methodName.Length;
31 for (int i = 0; i < 40 - length; i++)
32 {
33 methodName += " ";
34 }
35 Console.WriteLine(methodName +
36 " IsAscOrdered:" + IsAscOrdered(result) + " Time:" + stopwatch.Elapsed.TotalSeconds);
37
38 }
测试主体如下:

1 static void Main(string[] args)
2 {
3 int[] aa = RandomSet(50000, 99999);
4 //int[] aa = OrderedSet(5000);
5 Console.WriteLine("Array Length:" + aa.Length);
6 RunTheMethod((Action>)SelectSort, aa.Clone() as int[]);
7 RunTheMethod((Action>)BubbleSort, aa.Clone() as int[]);
8 RunTheMethod((Action>)BubbleSortImprovedWithFlag, aa.Clone() as int[]);
9 RunTheMethod((Action>)BubbleCocktailSort, aa.Clone() as int[]);
10 RunTheMethod((Action>)InsertSort, aa.Clone() as int[]);
11 RunTheMethod((Action>)InsertSortImprovedWithBinarySearch, aa.Clone() as int[]);
12 RunTheMethod((Action>)QuickSortStrict, aa.Clone() as int[]);
13 RunTheMethod((Action>)QuickSortRelax, aa.Clone() as int[]);
14 RunTheMethod((Action>)QuickSortRelaxImproved, aa.Clone() as int[]);
15 RunTheMethod((Func, IList>)MergeSort, aa.Clone() as int[]);
16 RunTheMethod((Action>)ShellSort, aa.Clone() as int[]);
17 RunTheMethod((Func, IList>)RadixSort, aa.Clone() as int[]);
18 RunTheMethod((Action>)HeapSort, aa.Clone() as int[]);
19 TestMicrosoft(aa.Clone() as int[]);
20 Console.Read();
21 }
22
23 public static void RunTheMethod(Func, IList> method, IList data)
24 {
25 Stopwatch stopwatch = new Stopwatch();
26 stopwatch.Start();
27 IList result = method(data);
28 stopwatch.Stop();
29 string methodName = method.Method.Name;
30 int length = methodName.Length;
31 for (int i = 0; i < 40 - length; i++)
32 {
33 methodName += " ";
34 }
35 Console.WriteLine(methodName +
36 " IsAscOrdered:" + IsAscOrdered(result) + " Time:" + stopwatch.Elapsed.TotalSeconds);
37 }
38
39 public static void RunTheMethod(Action> method, IList data)
40 {
41 Stopwatch stopwatch = new Stopwatch();
42 stopwatch.Start();
43 method(data);
44 stopwatch.Stop();
45 string methodName = method.Method.Name;
46 int length = methodName.Length;
47 for (int i = 0; i < 40 - length; i++)
48 {
49 methodName += " ";
50 }
51 Console.WriteLine(methodName +
52 " IsAscOrdered:" + IsAscOrdered(data) + " Time:" + stopwatch.Elapsed.TotalSeconds);
53 }

剩余代码折叠在此处
 View Code
View Code
测试设备:win8(64位),i7-3630QM,8G内存,vs2012
测试结果:
100000,50000,10000,5000,1000,100依次是:





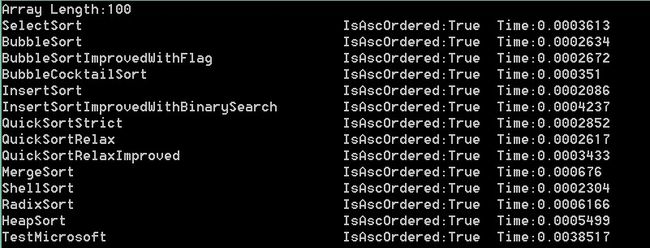
结果分析:可以看出在大数组的时候,微软自带排序更接近快速排序。而当数组变小时,速度却没有明显提升,甚至变得更慢,
比如1000和100。可以推断出在数组足够小的时候,比较已经不是影响这个方法主要因素。而根据它对大数组的表现。我们可以
推断出它应该用的是快速排序。反编译验证下:

在System.Linq.EnumerableSorter下。有兴趣的同学可以去看下详细实现。
维基上也有个测试。硬件没我的好。时间是我测试结果时间的几百倍。有兴趣的同学可以比较下。
在上面的测试中,我们可以看到快速最快,归并其次,冒泡最慢(维基上是希尔最快,估计使用的是某种神奇的步长)。
在我这里,以前实现的希尔还不如二分查找优化版的快,修正后希尔快了相当多,上面测试的希尔排序是以前错误的实现。
修正后的实现测试效果请点击右侧导航到希尔排序查看。希尔排序是一种神奇又有潜力的算法。步长不好会很挫!
而基数排序却是比平均时间复杂度为o(nlogn)的堆排序,归并排序,快速排序还要慢的,虽然它的平均时间复杂度为o(n)。
冒泡标识优化版对随机数列结果优化不明显,鸡尾酒版优化可以看到,但也不是很厉害。
插入排序二分查找优化版优化比较明显。我优化的快速排序QuickSortRelaxImproved优化也不明显。
以上是随机数列的测试结果,最大值为99999。
而对于有序数列,这些方法表现又会如何呢?
我这里就不演示了。本文末尾会附上demo,大家可以自行测试。
有意思的是:
我在测试有序数列的时候,QuickSortStrict方法栈溢出了(stack overflow exception)。这个异常
是让我去stackoverflow搜寻答案吗?哈哈!我确信我的方法不是无限循环。跳过一堆链接。。。我是
在测试10000个数排序的时候发生的错误。我跟踪后发现大约在9400多次递归的时候,栈溢出。找啊找
终于找见了一个类似的问题。上面说如果一个递归9000多次而没有返回值,也会报栈溢出的。而这个方法
对于10000个有序数列,确实每次减少一个数地递归,次数会超过限制。
我的算法理论不怎么好,对于时间复杂度和空间复杂度,还有稳定度,搞得也不怎么清楚,只知道个大致的
意思。各位要笔试面试的朋友可以去维基百科这个表来了解学习。
总结
我觉得使用IList更贴近数列,更能展现基本的操作。所以我的实现中都没有将它强制转化为List
或者int[]来调用微软封装的方法。这样说来,题目说C#实现倒快有点名不副实了。不过这样却也方便了其它语言
朋友。比如将我这篇博文里的实现随便改改,就可以说是另一个语言版本的8种排序算法了。哈哈!在这里,
我想说下这次学习排序对我的意义:老久不怎么动脑了,突然动起来,磨磨唧唧地得出结果,最后倒也有点成就感!
在学习过程中,经常会脑子转不过弯,想不通的,只是走在路上或者睡觉前突然灵感一现,有点小惊喜的感觉!
这大概就是进步的特征吧!哈哈!这次写demo+写博客花费了不少时间,倒也收获颇多,尤其在我将8种
排序都实现之前,没进行过一次测试,全部实现完成后,测试时各种索引越界+无限循环+各种问题,没几个
能跑通的,到后来的几乎都没有问题,也算是锻炼了思维,找出错原因的能力。本篇是自我学习的一个总结,
要学习及锻炼的园友,还望一定自己实现一下,可以和我的比较一下,解除疑惑或者提出改进。
主要参考:维基百科,有趣的演示
Demo源码
![]()
![]()
![]() View Code
View Code
![]()
![]()
![]()
![]()
![]()
![]()
![]()