生成树专题
cover by 一堆大佬的博客 百度百科等#%¥%~
反正不是我写的
首先 让我们先了解一下生成树的概念
生成树
在图论中,如果连通图 的一个子图是一棵包含 的所有顶点的树,则该子图称为G的生成树(SpanningTree)。
生成树是连通图的包含图中的所有顶点的极小连通子图。
图的生成树不惟一。从不同的顶点出发进行遍历,可以得到不同的生成树
通俗的来说,生成树就是
只要能连通所有顶点而又不产生回路的任何子图都是它的生成树
连接图中所有的点n,并且只有n-1条边的子图就是它的生成树
——————————————————————————————————————
常用的生成树算法有DFS生成树、BFS生成树、PRIM 最小生成树和Kruskal最小生成树算法
通常,由深度优先搜索得到的生成树称为深度优先生成树,简称为DFS生成树;由广度优先搜索得到的生成树称为广度优先生成树,简称为BFS生成树
深度优先生成树具体有什么好处我也不太清楚,可能比较好打(口胡)
广度优先生成树是所有生成树中高度最低的(显然)
![]()
接下来进入正题
在所有生成树中,应用最广泛的当然是
——————————————————————————————————————
最小生成树
- 在生成树中,我们称生成树各边权值和为该树的权。对于无向连通图来说,权值最小的生成树被成为最小生成树。
这个也是图论的基础,能够配合图论其他多中算法使用
在此先引入一个别的概念
———————————————————————————————————————
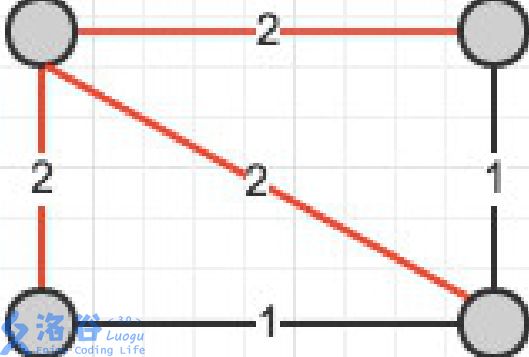
瓶颈生成树
无向图G的一颗瓶颈生成树是这样的一颗生成树T,它最大的边权
值在G的所有生成树中是最小的。瓶颈生成树的值为T中最大权值边的权。
结论
无向图的最小生成树一定是瓶颈生成树,但瓶颈生成树
不一定是最小生成树
怎么证明呢?
可以使用反证法
假设最小生成树不是瓶颈树,设最小生成树T的最大权边为e,则
存在一棵瓶颈树Tb,其所有的边的权值小于w(e)。删除T 中的e,形成
两棵数T1,T2,用Tb中连接T1,T2的边连接这两棵树,得到新的生成树,
其权值小于T,与T是最小生成树矛盾
通俗的来说呢,就是先假设结论错误,即最小生成树的最大边比瓶颈生成树的最大边大,然后删掉最小生成树的最大边,这时候最小生成树会被分成两个部分(两颗树),那么,在瓶颈生成树中肯定存在连接这两个部分并且比最小生成树最大边小的边(因为毕竟瓶颈生成树人家也是生成树,任意两个部分是肯定有边相连的),那么用这条边替换掉最小生成树的最大边,就会与最小生成树的定义矛盾
应该很容易理解才对
接下来,瓶颈生成树不一定是最小生成树
不多说,直接上图
感性理解
——————————————————————————————————————
知道了这个结论之后,像找最短路中最大权值的题应该就很好做了吧
那么,我们如何来求最小生成树呢?
1.kruskal算法
Kruskal 算法是能够在O(mlogm) 的时间内得到一个最小生成树的算
法。它主要是基于贪心的思想:
① 将边按照边权从小到大排序,并建立一个没有边的图T。
② 选出一条没有被选过的边权最小的边。
③ 如果这条边两个顶点在T 中所在的连通块不相同,那么将
它加入图T。
④ 重复②和③直到图T 连通为止。
由于只需要维护连通性,可以不需要真正建立图T,可以用并查集
来维护。
观察一下几种不同风格的代码
#include
#include
using namespace std;
int n,m,x,y,z,f1,f2,tot,k,fa[1001];
struct node{
int x,y,v;
}a[10001];
int cmp(const node &a,const node &b)
{
return a.v ——————————————————————————————
/*
* 克鲁斯卡尔(Kruskal)最小生成树
*/
void kruskal(Graph G)
{
int i,m,n,p1,p2;
int length;
int index = 0; // rets数组的索引
int vends[MAX]={0}; // 用于保存"已有最小生成树"中每个顶点在该最小树中的终点。
EData rets[MAX]; // 结果数组,保存kruskal最小生成树的边
EData *edges; // 图对应的所有边
// 获取"图中所有的边"
edges = get_edges(G);
// 将边按照"权"的大小进行排序(从小到大)
sorted_edges(edges, G.edgnum);
for (i=0; i2.prim算法
Prim 算法和Kruskal 算法一样也是寻找最小生成树的一种方法:
① 先建立一个只有一个结点的树,这个结点可以是原图中任
意的一个结点。
② 使用一条边扩展这个树,要求这条边一个顶点在树中另一
个顶点不在树中,并且这条边的权值要求最小。
③ 重复步骤②直到所有顶点都在树中。
这里记顶点数v,边数e
邻接矩阵:O(v) 邻接表:O(elog2v)
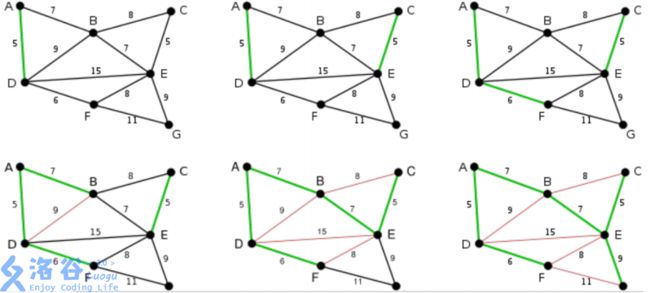
此为原始的加权连通图。每条边一侧的数字代表其权值。
顶点D被任意选为起始点。顶点A、B、E和F通过单条边与D相连。A是距离D最近的顶点,因此将A及对应边AD以高亮表示。
不可选 C, G 可选A, B, E, F 已选 D
下一个顶点为距离D或A最近的顶点。B距D为9,距A为7,E为15,F为6。因此,F距D或A最近,因此将顶点F与相应边DF以高亮表示。
不可选 C G,可选B, E, F,已选A,D
算法继续重复上面的步骤。距离A为7的顶点B被高亮表示。
可选 B,E,G 不可选 C,已选 A D F
在当前情况下,可以在C、E与G间进行选择。C距B为8,E距B为7,G距F为11。点E最近,因此将顶点E与相应边BE高亮表示
可选 C E G,不可选 无,已选 A D B F
接下来继续进行,我就不打具体步骤了
结束
现在,所有顶点均已被选取,图中绿色部分即为连通图的最小生成树。在此例中,最小生成树的权值之和为39
是不是有点像最短路算法中的迪杰斯特拉?
其实代码实现也差不多
最简单的无优化版本
+ View code
#include
#include
#include
using namespace std;
/*最小生成树Prim未优化版*/
int book[100];//用于记录这个点有没有被访问过
int dis[100];//用于记录距离树的距离最短路程
int MAX = 99999;//边界值
int maps[100][100];//用于记录所有边的关系
int main()
{
int i,j,k;//循环变量
int n,m;//输入的N个点,和M条边
int x,y,z;//输入变量
int min,minIndex;
int sum=0;//记录最后的答案
cin>>n>>m;
//初始化maps,除了自己到自己是0其他都是边界值
for (i = 1; i <= n; i++)
{
for (j = 1; j <= n; j++)
{
if(i!=j)
maps[i][j] = MAX;
else
maps[i][j] = 0;
}
}
for (i = 1; i <= m; i++)
{
cin>>x>>y>>z;//输入的为无向图
maps[x][y] = z;
maps[y][x] = z;
}
//初始化距离数组,默认先把离1点最近的找出来放好
for (i = 1; i <= n; i++)
dis[i] = maps[1][i];
book[1]=1;//记录1已经被访问过了
for (i = 1; i <= n-1; i++)//1已经访问过了,所以循环n-1次
{
min = MAX;//对于最小值赋值,其实这里也应该对minIndex进行赋值,但是我们承认这个图一定有最小生成树而且不存在两条相同的边
//寻找离树最近的点
for (j = 1; j <= n; j++)
{
if(book[j] ==0 && dis[j] < min)
{
min = dis[j];
minIndex = j;
}
}
//记录这个点已经被访问过了
book[minIndex] = 1;
sum += dis[minIndex];
for (j = 1; j <= n; j++)
{
//如果这点没有被访问过,而且这个点到任意一点的距离比现在到树的距离近那么更新
if(book[j] == 0 && maps[minIndex][j] < dis[j])
dis[j] = maps[minIndex][j];
}
}
cout< 链式前项星存图
#include
using namespace std;
#define re register
#define il inline
il int read()
{
re int x=0,f=1;char c=getchar();
while(c<'0'||c>'9'){if(c=='-') f=-1;c=getchar();}
while(c>='0'&&c<='9') x=(x<<3)+(x<<1)+(c^48),c=getchar();
return x*f;
}//快读,不理解的同学用cin代替即可
#define inf 123456789
#define maxn 5005
#define maxm 200005
struct edge
{
int v,w,next;
}e[maxm<<1];
//注意是无向图,开两倍数组
int head[maxn],dis[maxn],cnt,n,m,tot,now=1,ans;
//已经加入最小生成树的的点到没有加入的点的最短距离,比如说1和2号节点已经加入了最小生成树,那么dis[3]就等于min(1->3,2->3)
bool vis[maxn];
//链式前向星加边
il void add(int u,int v,int w)
{
e[++cnt].v=v;
e[cnt].w=w;
e[cnt].next=head[u];
head[u]=cnt;
}
//读入数据
il void init()
{
n=read(),m=read();
for(re int i=1,u,v,w;i<=m;++i)
{
u=read(),v=read(),w=read();
add(u,v,w),add(v,u,w);
}
}
il int prim()
{
//先把dis数组附为极大值
for(re int i=2;i<=n;++i)
{
dis[i]=inf;
}
//这里要注意重边,所以要用到min
for(re int i=head[1];i;i=e[i].next)
{
dis[e[i].v]=min(dis[e[i].v],e[i].w);
}
while(++totdis[i])
{
minn=dis[i];
now=i;
}
}
ans+=minn;
//枚举now的所有连边,更新dis数组
for(re int i=head[now];i;i=e[i].next)
{
re int v=e[i].v;
if(dis[v]>e[i].w&&!vis[v])
{
dis[v]=e[i].w;
}
}
}
return ans;
}
int main()
{
init();
printf("%d",prim());
return 0;
} 优先队列+堆优化
#include
#include
#include
#include
#define R register int
using namespace std;
int k,n,m,cnt,sum,ai,bi,ci,head[5005],dis[5005],vis[5005];
struct Edge
{
int v,w,next;
}e[400005];
void add(int u,int v,int w)
{
e[++k].v=v;
e[k].w=w;
e[k].next=head[u];
head[u]=k;
}
typedef pair pii;
priority_queue ,greater > q;
void prim()
{
dis[1]=0;
q.push(make_pair(0,1));
while(!q.empty()&&cnt 这是啥。。。
#include
#include
#include
#include
using namespace std;
int n,m,x,y,z,tot,ans,k,ds[1001],next[2001],st[1001],to[2001],cost[2001];
bool vis[1001];
void addedge(int x,int y,int z)
{
next[++tot]=st[x];st[x]=tot;to[tot]=y;cost[tot]=z;
}
struct node
{
int x,d;
node(int a,int b):x(a),d(b) {}
bool operator<(const node&t) const {return d>t.d;}
}; priority_queueq;
int main()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=m;i++)
{
scanf("%d%d%d",&x,&y,&z);
addedge(x,y,z);addedge(y,x,z);
}
memset(ds,0x7f,sizeof(ds));
ds[1]=0;q.push(node(1,0));vis[0]=1;
for(int i=1;i<=n;i++)
{
node a(0,0);
while(vis[a.x]&&!q.empty())
a=q.top(),q.pop();
if(vis[a.x]) break;
ans+=a.d;vis[a.x]=1;k++;
for(int j=st[a.x];j;j=next[j])
{
y=to[j];z=cost[j];
if(!vis[y]&&z ## kruskal和prim的比较
从策略上来说,Prim算法是直接查找,多次寻找邻边的权重最小值,而Kruskal是需要先对权重排序后查找的~
所以说,Kruskal在算法效率上是比Prim快的,因为Kruskal只需一次对权重的排序就能找到最小生成树,而Prim算法需要多次对邻边排序才能找到~
prim:该算法的时间复杂度为O(n2)。与图中边数无关,该算法适合于稠密图。
kruskal:需要对图的边进行访问,所以克鲁斯卡尔算法的时间复杂度只和边又关系,可以证明其时间复杂度为O(eloge)。适合稀疏图
接下来讲几道例题
[UVALive 6437]Power Plant
T组数据,给定一幅带权图(n, m), 然后给定k个点, 与图中存在有若
干条边。每个点都要至少要和这k个点的一个点直接或间接相连, 问最少
的距离是多少。
1 ≤ T ≤ 100,
k个点,至少一个,明显的缩点。
[UVA 1151]Buy or Build
平面上有n个点,你的任务是让所有n个点连通,为此,你可以新建
一些边,费用等于两个端点的欧几里得距离的平方。另外还有q个套餐,
可以购买,如果你购买了第i个套餐,该套餐中的所有结点将变得相互
连通,第i个套餐的花费为ci。求最小花费。
1 ≤ n ≤ 1000, 0 ≤ q ≤ 8。
枚举选择哪个套餐后再求最小生成树即可。
[UVA 10369]Arctic Network
南极有n个科研站,要用卫星或无线电把他们连起来,无线电的费
用随着距离增加而增加,并且长传播距离为d,现在有s个卫星,任意两
个安装了卫星的设备无论距离多远都可以直接通信,求一个方案使
得d最小。
s ≤ 1时求最小生成树即可
s ≥ 2时,等于孤立了s − 1个区域,即s − 1条边置为0,当然是最小
生成树中最大的s − 1条。
kruskal的过程中直接计算即可。
[BZOJ 1601][Usaco2008 Oct]灌水
Farmer John已经决定把水灌到他的n(1¡=n¡=300)块农田,农田被数
字1到n标记。把一块土地进行灌水有两种方法,从其他农田饮水,或者
这块土地建造水库。建造一个水库需要花费wi
,连接两块土地需要花
费pij。计算Farmer John所需的最少代价。
1 ≤ N ≤ 300, 1 ≤ wi ≤ 105
, 1 ≤ pij ≤ 105。
每个水库要么选择自己这里建造水库,要么选择连一条边到已建成
的水库。
假设所有的水库最终都选择好了一个决策的话,那么整个图就是,
分成m块,每一块有一个点是自己建造水库的。其他都是顺着边连到这
个点的。也就是在这个子图当中做最小生成树。
加一个超级源,每个点向源连花费wi边。然后在整个图中做最小生
成树。超级源的连通保证了至少有一个点建造了水库
还有一些比较难的题,等我自己搞懂了再补吧~
完结撒花