《数字图像处理》第九章 形态学图像处理 学习笔记附部分例子代码(C++ & opencv)

0. 前言

参考博客：
opencv图像处理模块(6)——击中击不中 - 知乎 (zhihu.com)

第三版教材中图片下载地址： book images downloads

vs2019配置opencv可以查看：VS2019 & Opencv4.5.4配置教程

前情回顾：
数字图像处理第三章 灰度变换和空间滤波 学习笔记
数字图像处理第四章 频率域滤波 学习笔记
数字图像处理第五章 图像复原和重建（内容较简单，就没有详细记录笔记）
数字图像处理第六章 彩色图像处理
数字图像处理第七章 小波与多分辨率处理（内容困难，仅进行了简单记录）
数字图像处理第八章 图像压缩（目前非重点）

后续剧情：
数字图像处理第十章 图像分割 学习笔记
数字图像处理第11章 表示和描述 学习笔记

1. 腐蚀和膨胀

1.1 腐蚀

$$A\ominus B=\{z|(B{)}_z\cap A^c=\varnothing \}$$

B不与A的补集的交集为空

1.2 膨胀

$$A\oplus B=\left\{z\mid (\hat{B}{)}_z\cap A\ne \varnothing \right\}$$

A是被膨胀的集合, A和B至少有一个元素重合

1.3 对偶性

膨胀和腐蚀关于集合求补运算和反射运算是对偶的.

2. 开操作和闭操作

开操作: 平滑物体的轮廓, 断开较窄的狭颈并消除细的突出物.

闭操作: 弥合较窄的间断和细长的沟壑, 消除小的孔洞, 填补轮廓线中的断裂.

结构元B对集合A的开操作：

$$A\circ B=(A\ominus B)\oplus B$$

结构元B对集合A的闭操作：

$$A\bullet B=(A\oplus B)\ominus B$$

opencv有腐化函数erode()和膨胀函数dilate()

Mat openOperationRes(Mat input, int size) {
    Mat kernel = Mat::ones(Size(size, size), CV_8U);
    //先腐化再膨胀
    Mat eroded;
    erode(input, eroded, kernel);
    Mat opened;
    dilate(eroded, opened, kernel);
    return opened;
}

Mat closeOperationRes(Mat input, int size) {
    Mat kernel = Mat::ones(Size(size, size), CV_8U);
    //先膨胀再腐化
    Mat dilated;
    dilate(input, dilated, kernel);
    Mat closed;
    erode(dilated, closed, kernel);
    return closed;
}

void test05(string path) {
    Mat img = imread(path, IMREAD_GRAYSCALE);
    if (img.empty()) {
        cout << "Unable to load image\n";
        return;
    }
    Mat kernel = Mat::ones(Size(3, 3), CV_8U);
    //进行腐化操作
    Mat eroded;
    erode(img, eroded, kernel);
    Mat opened = openOperationRes(img, 3);
    Mat opened_closed = closeOperationRes(opened, 3);

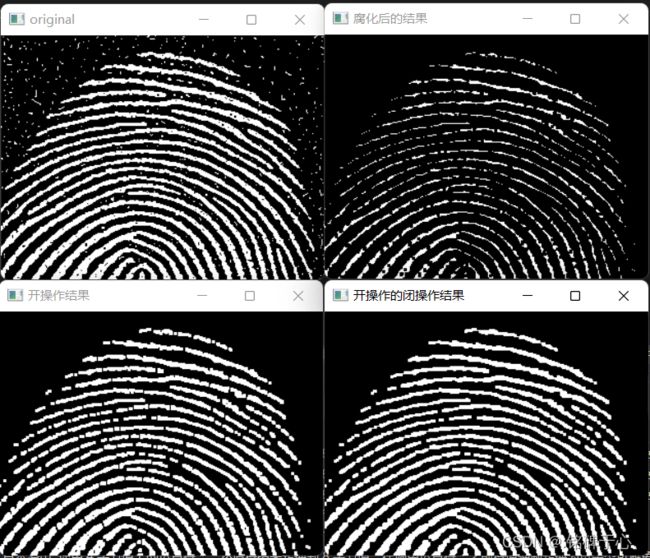
    imshow("original", img);
    imshow("腐化后的结果", eroded);
    imshow("开操作结果", opened);
    imshow("开操作的闭操作结果", opened_closed);
    waitKey(0);
}

3. 击中或不击中变换

形态学上的击中或不击中是形状检测中的一个基本工具。

$$A⊛B=(A\ominus B_1)\cap (A^c\ominus B_2)$$

其中，令B=(B1, B2)，B1表示需要匹配的结构元素构成的集合，B2表示不需要存在的结构元素所构成的集合。通过这样进行需要特征的提取和不需要特征的“抛弃”。

4. 一些基本的形态学算法

4.1 边界提取

在处理二值图像时，效果好

void test06(string path) {
    Mat image = imread(path, IMREAD_GRAYSCALE);
    if (image.empty()) {
        cout << "Unable to load the image\n";
        return;
    }
    Mat kernel = Mat::ones(Size(3, 3), CV_8U);
    //进行腐化操作
    Mat eroded;
    erode(image, eroded, kernel);

    imshow("边缘提取", image - eroded);
    waitKey(0);
}

4.2 孔洞填充

下例代码针对该公式：

$$X_k=(X_{k-1}\oplus B)\cap A^{c}k=1,2,3,\cdots$$

当然有逆向思维再里面，先将不是孔洞的部分膨胀满，再取反。

void test07(string path) {
    Mat image = imread(path, IMREAD_GRAYSCALE);
    if (image.empty()) {
        cout << "Unable to load the Image\n";
        return;
    }

    //1. 使用floodFill函数
    Mat closedImg = closeOperationRes(image, 3);

    Mat floodFillImg = image.clone();
    floodFill(floodFillImg, cv::Point(0, 0), Scalar(255));

    // Invert floodfilled image
    Mat im_floodfill_inv;
    bitwise_not(floodFillImg, im_floodfill_inv);

    // Combine the two images to get the foreground.
    Mat im_out = (image | im_floodfill_inv);

    //2. 孔洞填充
    //先将画布置全黑，再根据原图取反来得到x0
    Mat xk_1 = Mat::zeros(Size(image.cols, image.rows), CV_8U);
    Mat xk = Mat::zeros(Size(image.cols, image.rows), CV_8U);
    Mat ac = ~image;
    Mat B = (Mat_<uchar>(3, 3) << 0, 1, 0, 1, 1, 1, 0, 1, 0);


    //从(0,0)开始进行膨胀，这个位置不能是原图孔洞待的位置
    //当然可以多弄几个点开始，减少迭代次数
    xk_1.at<uchar>(0, 0) = 255; 

    int cnt = 0;
    while     (true) {
        dilate(xk_1, xk, B);    //对xk-1进行膨胀操作
        bitwise_and(xk, ac, xk);//与AC进行与操作

        Mat diff = xk != xk_1;    //元素相同，diff对应位置置为0
        int count = countNonZero(diff);    //当diff所有元素都为0时（俩个矩阵相等）
        if (count == 0)
            break;

        xk.copyTo(xk_1);    //将xk的值拷贝给xk-1, 不能直接xk_1 = xk(两个变量的地址和值都一致， 修改其中一个变量，另一个变量也跟着动)
        cnt++;
    }
    Mat result = ~xk;

    imshow("原图", image);
    imshow("floodfill结果", im_out);
    imshow("x" + to_string(cnt), result);
    waitKey(0);
}

总共迭代了1005次，才填充完毕

5. 形态学重建

5.1 测地膨胀和腐蚀

令F表示为标记图像，令G表示为模版图像。标记图像相对于模版的大小为1的测地膨胀定义为：

$$D_G^{(1)}(F)=(F\oplus B)\cap G$$

而F相对于模版G的大小为1的测地腐蚀定义为：

$$E_G^{(1)}(F)=(F\ominus B)\cup G$$

void displayImg(Mat input, string windowName) {
    Mat result;
    normalize(input, result, 0, 255, NORM_MINMAX);
    result.convertTo(result, CV_8U);
    namedWindow(windowName, WINDOW_KEEPRATIO);//表示可以修改窗体的大小
    imshow(windowName, result);
}
void test08(string path) {

    Mat image = imread(path, IMREAD_GRAYSCALE);
    if (image.empty()) {
        cout << "Unable to load the Image\n";
        return;
    }

    Mat kernel = Mat::ones(Size(1, 51), CV_8U);
    Mat eroded;
    erode(image, eroded, kernel);
    Mat xk_1;
    dilate(eroded, xk_1, kernel);

    displayImg(xk_1, "开操作结果");
    //再进行重建
    Mat B = Mat::ones(Size(3, 3), CV_8U);
    Mat xk = Mat::zeros(Size(image.cols, image.rows), CV_8U);
    int cnt = 0;
    while (true) {
        dilate(xk_1, xk, B);
        bitwise_and(xk, image, xk);   //一样的套路，膨胀再取交集

        Mat diff = xk_1 != xk;
        if (countNonZero(diff) == 0)
            break;

        xk.copyTo(xk_1);
        cnt++;
    }

    displayImg(image, "原图");
    displayImg(xk, "重建解雇xk" + to_string(cnt));

    waitKey(0);
}

实例代码如上，重建开操作要求至少一次腐蚀，使用相同的结构元计算开操作，接着进行重建操作。

6. 灰度级形态学

6.1 腐蚀和膨胀

结构元素b对一幅图像f在位置(x,y)处的腐蚀如下式所示，即求3×3区域中最小值

$$[f\ominus b](x,y)=\underset{(s,t)\in b}{\min }\{f(x+s,y+t)\}$$

而膨胀如下，求3×3区域中的最大值

$$[f\oplus b](x,y)=\underset{(s,t)\in b}{\max }\{f(x-s,y-t)\}$$

在opencv中使用的依旧是erode()和dilate()

开运算和闭运算也是一样

6.2 一些基本算法

形态学平滑： 使用平坦圆盘结构元对原始图像进行开操作，再进行闭操作

Mat openOperationRes(Mat input, Mat kernel = Mat::ones(Size(3, 3), 0));
Mat closeOperationRes(Mat input, Mat kernel = Mat::ones(Size(3, 3), 0));

void test09(string path) {
    Mat img = imread(path, IMREAD_GRAYSCALE);
    if (img.empty()) {
        cout << "Unable to load the image\n";
        return;
    }
    vector<Mat> vk;
    //使用函数直接构建结构元，可以使用cout查看结构元的形状
    Mat kernel1 = getStructuringElement(MORPH_ELLIPSE, Size(1, 1));
    Mat kernel2 = getStructuringElement(MORPH_ELLIPSE, Size(3, 3));
    Mat kernel3 = getStructuringElement(MORPH_ELLIPSE, Size(5, 5));
    vk.push_back(kernel1);
    vk.push_back(kernel2);
    vk.push_back(kernel3);

    displayImg(img, "原图");
    Mat input;
    img.copyTo(input);
    for (int i = 0; i < 3; i++) {
        Mat opened = openOperationRes(input, vk[i]);
        Mat closed = closeOperationRes(opened, vk[i]);
        closed.copyTo(input);
        displayImg(closed, "第" + to_string(i + 1) + "次操作结果");
    }

    waitKey(0);

}

Mat openOperationRes(Mat input, Mat kernel) {
    //Mat kernel = Mat::ones(Size(size, size), CV_8U);
    //先腐蚀再膨胀
    Mat eroded;
    erode(input, eroded, kernel);
    Mat opened;
    dilate(eroded, opened, kernel);

    return opened;
}

Mat closeOperationRes(Mat input, Mat kernel) {
    //Mat kernel = Mat::ones(Size(size, size), CV_8U);
    //先膨胀再腐蚀
    Mat dilated;
    dilate(input, dilated, kernel);
    Mat closed;
    erode(dilated, closed, kernel);

    return closed;
}

形态学梯度： $g=(f\oplus b)-(f\ominus b)$

顶帽变换和底帽变换：

• 顶帽变换：$T_{hat}(f)=f-(f\circ b)$

• 底帽变换：$B_{hat}(f)=(f\bullet b)-f$

纹理分割：

Mat getMorpGradient(Mat input, Mat kernel = Mat::ones(Size(3, 3), 0));
Mat getMorpGradient(Mat input, Mat kernel) {
    Mat dilated;
    dilate(input, dilated, kernel);
    Mat eroded;
    erode(input, eroded, kernel);

    return dilated - eroded;
}

void test10(string path) {
    Mat img = imread(path, IMREAD_GRAYSCALE);
    if (img.empty()) {
        cout << "Unable to load the image\n";
        return;
    }

    Mat kernel1 = getStructuringElement(MORPH_ELLIPSE, Size(61, 61));
    Mat kernel2 = getStructuringElement(MORPH_ELLIPSE, Size(121, 121));
    //Mat kernel1 = Mat::ones(Size(61, 61), CV_8U);
    //Mat kernel2 = Mat::ones(Size(121, 121), CV_8U);
    Mat closed = closeOperationRes(img, kernel1);
    Mat opened = openOperationRes(closed, kernel2);

    Mat border = getMorpGradient(opened);    //形态学梯度

    displayImg(img, "原图");
    displayImg(closed, "图b");
    displayImg(opened, "图c");
    displayImg(img + border, "分割结果");
    waitKey(0);
}

6.3 灰度级形态学重建

令f和g分别代表标记图像和模版图像，f可以是经受过腐蚀或者膨胀的图

测地膨胀定义为：

$$D_g^{(1)}(f)=(f\oplus b)\wedge g$$

f关于g的大小为n的测地膨胀定义为

$$D_g^{(n)}(f)=D_g^{(1)}[D_g^{(n-1)}(f)]$$

当$D_g^{(k)}(f)=D_g^{(k+1)}$时，相当于重构完毕，测地腐蚀定义类似.

实例： 将复杂的背景均匀化

• 图b：只用1x71的结构元对图a进行开操作，然后得到重建结果。

• 图c：用相同的线仅对原图进行开操作，可以看到图b的背景分布更加均匀(特别是按钮之间的部分)

• 图d：图a减图b的结果（顶帽操作）

• 图e：标准的顶帽操作（图a减图c）

• 图f：对图d进行开操作，该结果作为标记图像，图d作为模版图像，进行重建

• 图g：对图f进行膨胀操作

• 图h：图d和图g进行最小操作的结果（这个时候发现SIN中的I消失了），背景已经很好的均匀化了

• 图i：图g作为标记图像，图d作为模版图像，进行重建（本例的代码如下所示）

Mat reconGrayScale(Mat input, Mat original, int& cnt, Mat elem = Mat::ones(Size(3, 3), 0));
Mat reconGrayScale(Mat input, Mat original, int& cnt, Mat elem) {
	int count = 0;
	Mat xk_1 = input.clone();
	Mat xk;
	while (true) {
		Mat dilated;
		dilate(xk_1, dilated, elem);
		xk = min(dilated, original);
		count++;
		Mat diff = xk_1 != xk;
		if (countNonZero(diff) == 0)
			break;
		xk.copyTo(xk_1);
	}
	cnt = count;
	cout << "重构完毕, 迭代次数为" << count << endl;
	return xk;
}

void test11(string path) {
	Mat img = imread(path, IMREAD_GRAYSCALE);
	if (img.empty()) {
		cout << "Unable to load the image\n";
		return;
	}
	int cnt1;
	int cnt2;
	int cnt3;
	Mat element = Mat::ones(Size(71, 1), 0);
	Mat opened = openOperationRes(img, element);
	Mat reconOpened = reconGrayScale(opened, img, cnt1);//迭代了482次
	//cout << "重构完毕\n";
	Mat topHatImg;
    //开操作和闭操作也有专门的函数
	morphologyEx(img, topHatImg, MORPH_TOPHAT, element);

	Mat img_d = img - reconOpened;
	Mat element2 = Mat::ones(Size(11, 1), 0);
	Mat opened2 = openOperationRes(img_d, element2);
	Mat img_f = reconGrayScale(opened2, img_d, cnt2);//迭代了113次
	//Mat img_f = openOperationRes(img_d, element2);
	Mat img_g;
	dilate(img_f, img_g, Mat::ones(Size(21, 1), 0));

	Mat img_h = min(img_d, img_g);
	Mat img_i = reconGrayScale(img_g, img_d, cnt3);//迭代了121次

	displayImg(img, "original 11");
	displayImg(opened, "1x71结构元的开操作结果");
	displayImg(topHatImg, "顶帽操作");
	displayImg(reconOpened, "重建开操作" + to_string(cnt1)); 
	//displayImg(reconTophat, "重建顶帽操作" + to_string(cnt2));
	displayImg(img_d, "图d");
	displayImg(img_f, "图f: 用1x11的水平线对图d进行开操作" + to_string(cnt2));
	displayImg(img_g, "图g: 1x21的结构元对图f进行膨胀操作");
	displayImg(img_h, "图h：图d和图g进行最小操作");
	displayImg(img_i, "图i: 最终的重构图像" + to_string(cnt3));
	waitKey(0);
}

7. 小总结

重建是形态学中重要的一个算法。针对二值图像和灰度图像，有略微区别。

重建的步骤：

• 确定好标记图像、模版结构和重建结构元(一般就是正方形结构或者平坦圆盘结构)
• 规定迭代结束时刻的判断。