Matlab二维绘图
低级绘图命令line
有什么点就点哪里,然后连起来,没什么细节,不光滑,所以基本不会用到。
x=0:0.2*pi:2*pi;
y=sin(x);
line(x,y);%画一条sin函数线
line([-5,5],[2,2]);%画一条水平线
line([5,5],[0,2]);%画一条竖线高级绘图命令plot
没有定细节的时候跟line长得是一样的,但可以确定更多的细节。这种用的是最多的,一个例子就能举例说清楚全部常用函数是怎么用的。
x=0:0.02*pi:2*pi;
y1=sin(x);
y2=sin(2*x);
y3=sin(x+pi/2);
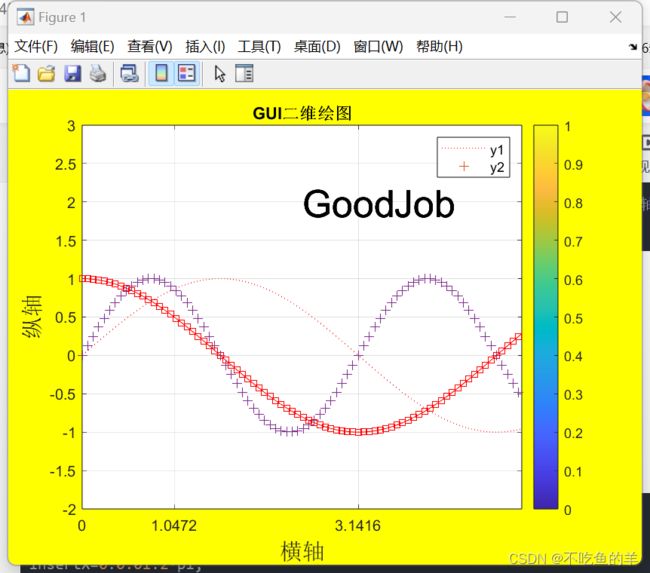
plot(x,y1,'r:',x,y2,'+');%画一条sin函数线
hold on;%保持图形,不让后面画的图形覆盖之前画的图形
plot(x,y3,'-rs');%指定线型为实线,颜色为红色,数据点标记为方形
legend('y1','y2');%添加图例
legend('show');%显示图例off是清除hide是隐藏
colorbar;%添加颜色条
title('GUI二维绘图','FontWeight','Bold');%添加标题,字体设置为黑体
xlabel('横轴','FontSize',15);%X轴注释
ylabel('纵轴','FontSize',15);%Y轴注释
axis([0 5 -2 3]);%调整坐标轴范围X轴0到5,Y轴-2到3
axis('xy');%使用笛卡尔坐标系
axis('on');%打开网格线、坐标、注释
%axis也可以一次性加多个字符串
%axis([0 5 -2 3],'xy','on');
grid on;%添加网格线
text(2.5,2,'GoodJob','FontSize',25);%在(2.5,2)的位置加上文字
set(gca,'XTick',[0 1/3*pi pi]);%gca是当前坐标轴对象的句柄,XTick设置的是X轴刻度
set(gcf,'color','y');%gcf是当前当前图像对象的句柄,把背景颜色设置为黄色效果如下图
样条函数spline
通过插值,将数据变化显得更加详细。
x=0:0.2:2*pi;
y=sin(x);
insertX=0:0.01:2*pi;
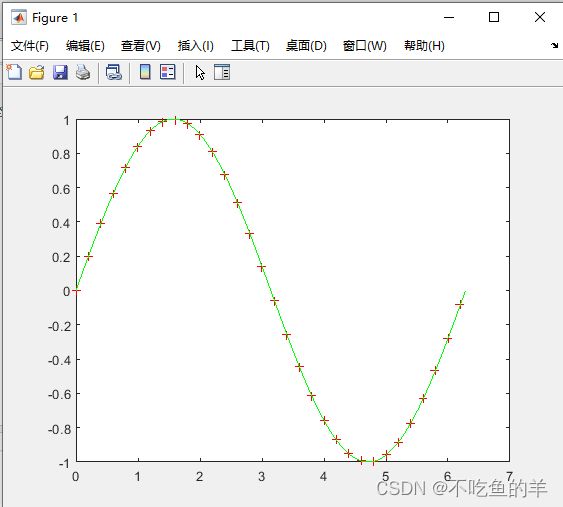
insertY=spline(x,y,insertX);
plot(x,y,'+r',insertX,insertY,'-g');子图subplot
就是创造一些子图,看一个例子就懂了。
x=-5:5;
subplot(2,1,1);%2行1列,选择第1个子图。子图跟矩阵不同,是横着数的。
y1=rand(size(x));
y2=normpdf(x);
hold;%hold on和hold off之间切换,默认是hold off,这里就会变成hold on
plot(x,y1,'b');
hold;%这里就会变成hold off,后面绘制的图形会把前面的覆盖掉
plot(x,y2,'r');
title('hold off');
subplot(2,1,2);%2行1列,选择第2个子图
plot(x,y1,'b');
hold on;%后面绘制的图形不会覆盖前面的
plot(x,y2,'r');
title('hold on');极坐标图polar
就是画个极坐标图,所以代码要用极坐标来算。
t=0:0.01*pi:2*pi;
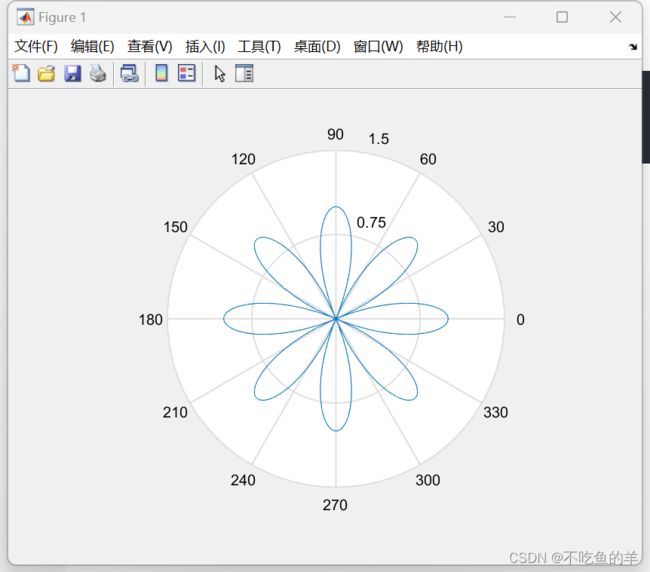
r=2*sin(2*(t-pi/8)).*cos(2*(t-pi/8));
polar(t,r);直角坐标系概率分布图
x=rand(500,1);%500*1矩阵
y=rand(500,3);%500*3矩阵
subplot(3,1,1);
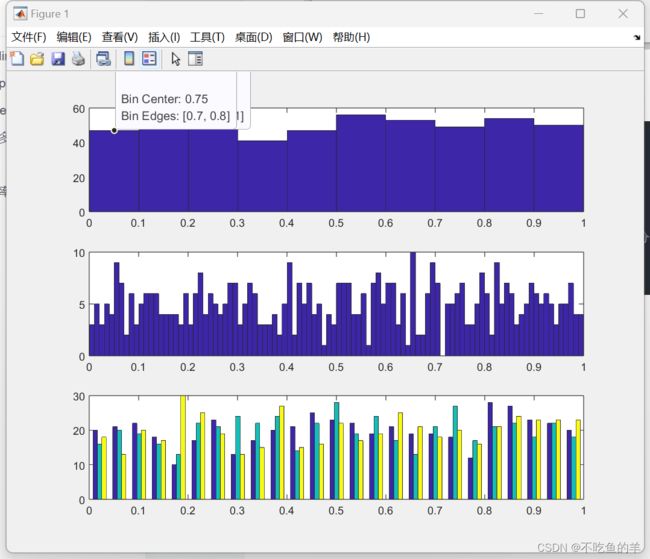
hist(x);%x里面最大值和最小值的差平均分为10等分
subplot(3,1,2);
hist(x,100);%x里面最大值和最小值的差平均分为100等分
subplot(3,1,3);
hist(y,25);%x里面最大值和最小值的差平均分为25等分画出来是这样的
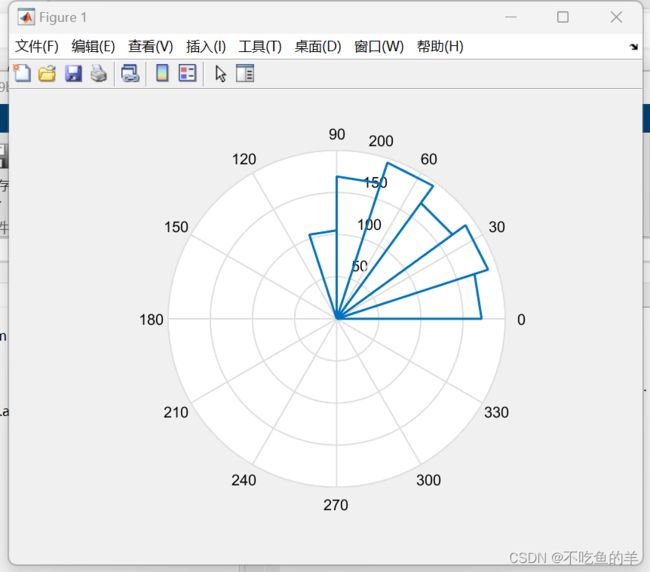
极坐标系概率分布图
因为长得像玫瑰,所以也叫玫瑰图。
x=rand(1000,1)*100;
t=x*pi/180;
rose(t);
set(findobj(gca,'Type','Line'),'LineWidth',1.5);柱状图
有两种,bar画横向柱状图,barh画纵向柱状图,格式如下:
bar(Y,option);%以1,2,3……为x坐标,option可选,下面的面积图等图形都有这个用法,不再赘述
bar(X,Y,option);%option如果为'stack'为累加式,如果为'group'为分组式例子如下
x=[3 5 6;4 8 7;6 9 7];
subplot(1,2,1);bar(x);
subplot(1,2,2);barh(x,'stack');面积图
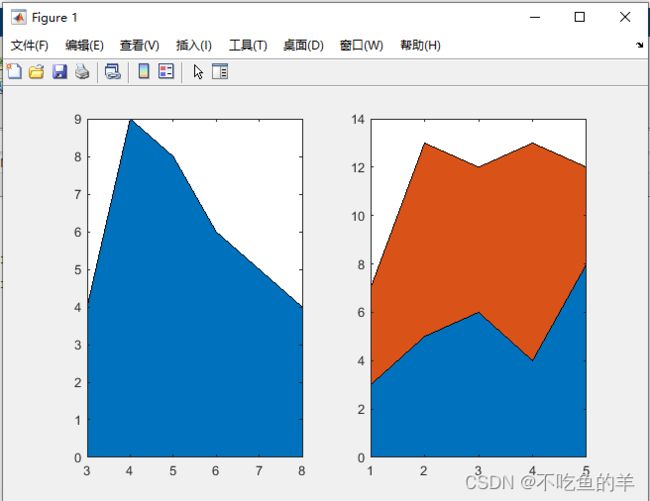
有个小小的注意点就是要数据要变成列
x=[3 5 6 4 8]';
y=[4 8 6 9 4]';
subplot(1,2,1);area(x,y);%只画一条
subplot(1,2,2);area([x,y]);%累叠模式饼状图
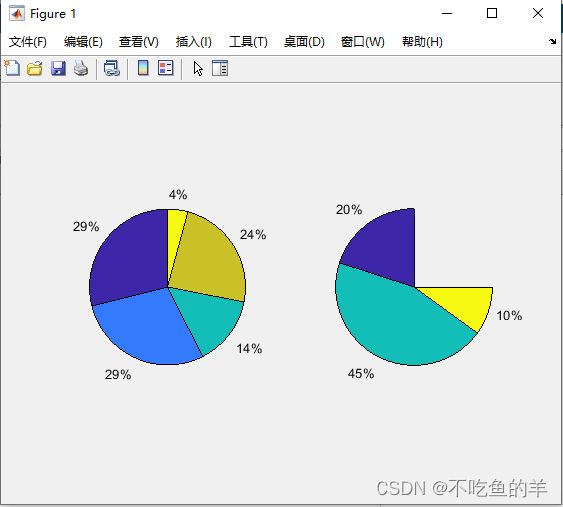
也就是计算个数据占比,不足100%的就空着。
x=rand(1,5);
y=[0.2 0.45 0.1];
subplot(1,2,1);pie(x);
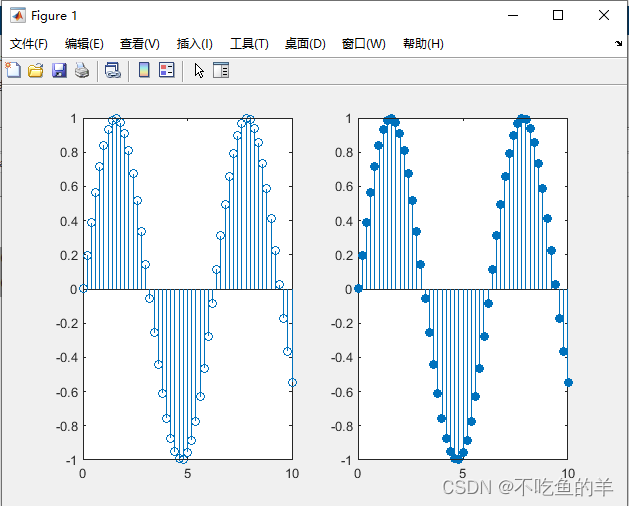
subplot(1,2,2);pie(y);离散数据绘图
x=0:0.2:10;
y=sin(x);
subplot(1,2,1);stem(x,y);%默认是空心小圆圈
subplot(1,2,2);stem(x,y,'fill');%画实心小圆圈阶梯图
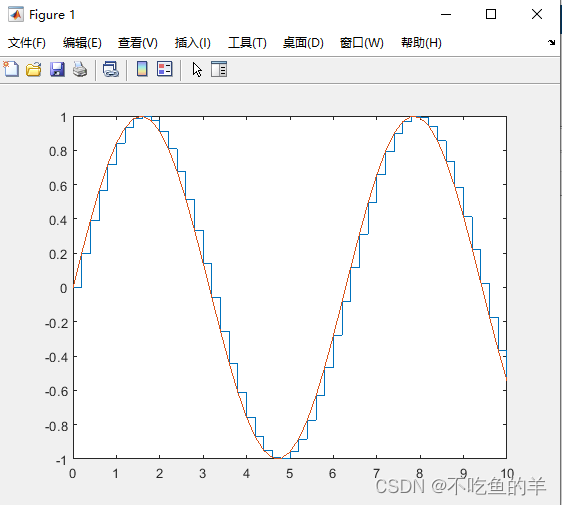
x=0:0.2:10;
y=sin(x);
stairs(x,y);
hold on;
plot(x,y);等高线图
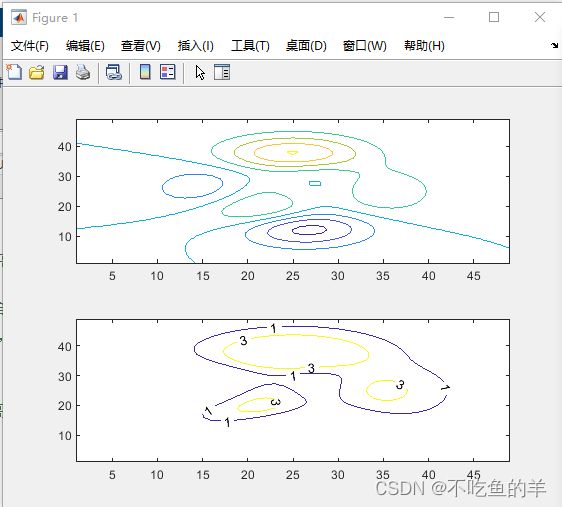
x=peaks;%生成的数据给到x
subplot(2,1,1);
contour(x);%绘制peaks图形等高线图,自动生成等高线
subplot(2,1,2);
[c,h]=contour(x,[3 1]);%c为等高矩阵,h为句柄列向量,指定等高线高度为3和1
clabel(c,h);%标注等高线标签,也就是等高线的数值
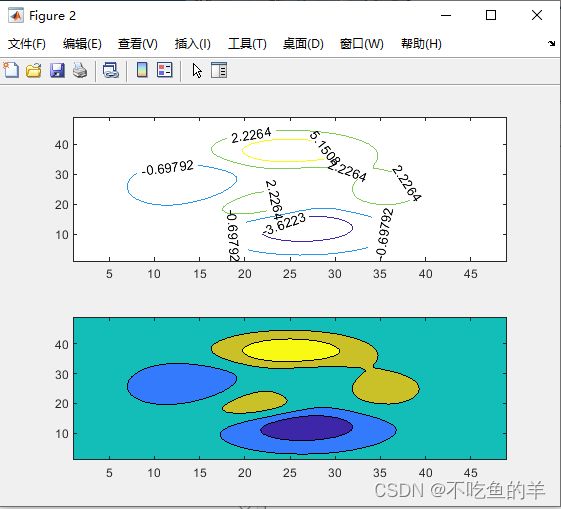
figure;%新建图形窗口
subplot(2,1,1);
[c,h]=contour(x,4);%指定等高线数量为4
clabel(c,h);
subplot(2,1,2);
contourf(x,4);%填充模式一共画了4个图
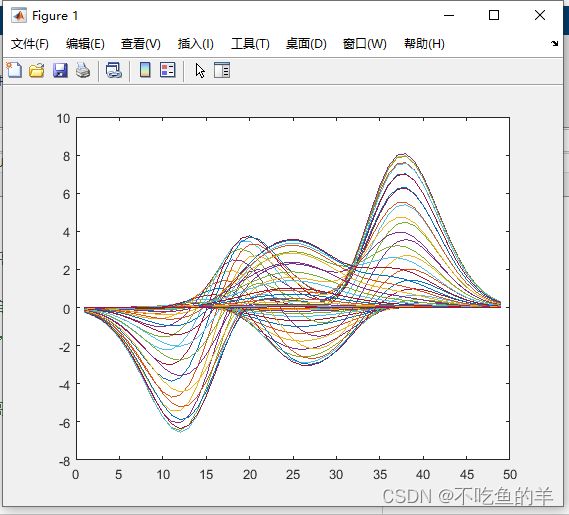
你会发现用plot(x)打印出来的图跟等高线图是对应上的,它的本质其实是个三维图,我们后面讲三维图会讲到。
向量图
常用向量图有罗盘图、羽毛球图、向量场图。
x=rand(2,5);
y=rand(2,5);
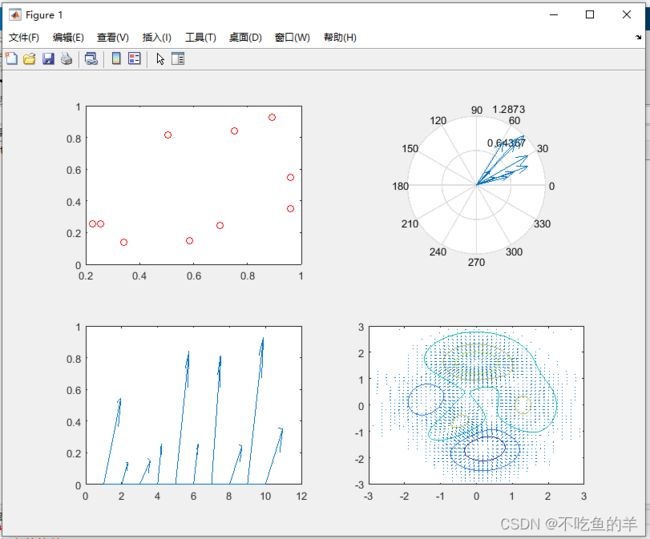
subplot(2,2,1);
plot(x,y,'ro');
subplot(2,2,2);
compass(x,y);%绘制罗盘图,起点在原点
subplot(2,2,3);
feather(x,y);%绘制羽毛球图,起点在X轴上间隔单位长度的刻度点
subplot(2,2,4);
[x,y,z]=peaks(50);
contour(x,y,z,5);%等高线
[u,v]=gradient(z);%梯度
hold on;
quiver(x,y,u,v);%绘制向量场图函数绘图
用M文件绘图
M文件定义
function y=Untitled(x)
y=exp(sin(x));执行命令
fplot('Untitled',[0 2*pi]);%将[0 2*pi]传入m文件执行效果
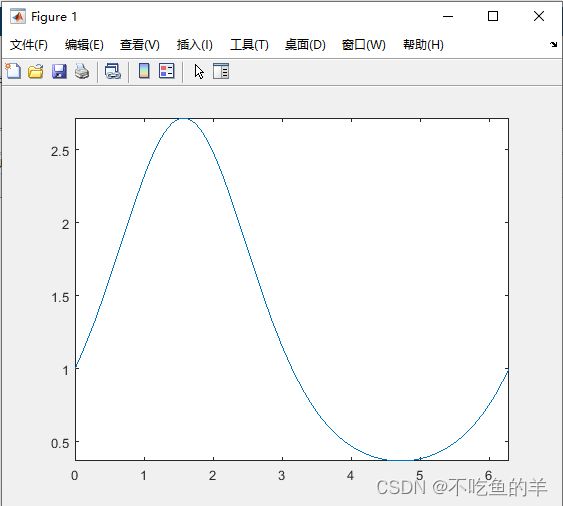
命令行窗口直接绘图
fplot('exp(sin(x))',[0 2*pi]);匿名函数
f=@(x)exp(sin(x))%@代表将f定义为函数指针,f的入参为x
fplot(f,[0 2*pi]);