洛谷 CSP-J 2021 分糖果+插入排序 个人解答的优化过程以及详解

首先声明这两道题目第一题很简单，读者可以不看解答自己先做一遍题目，看看能不能获得满分，我就是因为无意识考虑时间复杂度的问题没有获得满分最开始，然后我进行了优化，获得了满分，但是第二题的难度较大，读者可以仔细领会，接下来请看题目：

首先我们来看第一道题分糖果：

样例以及数据范围：

 我一开始的思路很简单，那就是从L到R进行枚举，不断更新ans得到最后的答案：

#include
using namespace std;
int n,L,R;
int ans=-1;
int main(){
	cin>>n>>L>>R;
	for(int i=L;i<=R;i++){
		ans=max(ans,i%n);
	}
	cout<

这段代码得不到满分，在极端的情况下会导致超时，不过如果不追求满分的同学的话可以使用，因为这段代码已经有九十分了，然后接下来我进行了优化，我来讲一下我的优化思路：因为很明显我们最后的答案就是1到n-1，所以我们可以考虑引入变量，然后计算出L和R模去n的值以及除去n的值，如果除去n的两个变量相减大于等于1就说明L和R的差必定大于等于n也就意味着存在一个值x属于L到R,让我分到n-1个苹果，亦或者L,R其中一个值模去n得到n-1的话，同样可以判断出能获得n-1个苹果，否则的话我们将模出来的两个变量从小到大进行枚举最后不断更新就可以得到我们想要的答案：

#include
using namespace std;
int n,L,R;
int ans=-1;
int main(){
	cin>>n>>L>>R;
	if(R-L>=n-1){
		cout<=1){
		cout<

好了，接下来是第二题，插入排序：

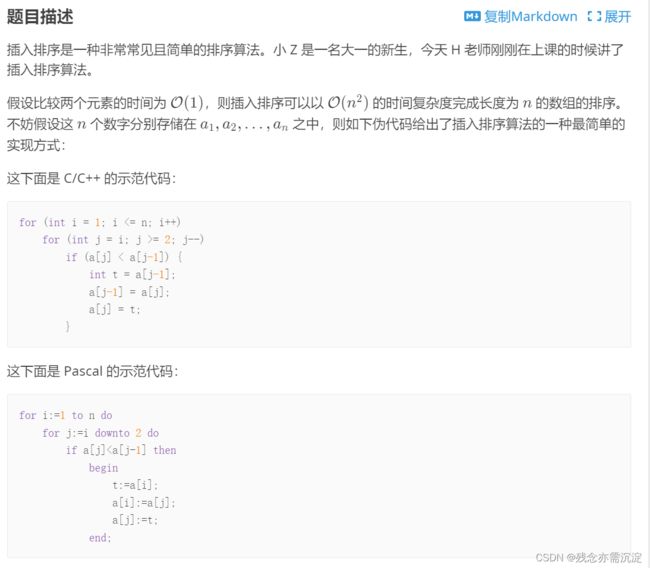
来看贼长的题干：

样例以及数据范围：

 

 好了接下来来分析一下这一道题目：
这道题目我一开始的想法也就是模拟，首先把该输入的输入了，只不过我们需要引入一个变量数组t，因为如果是操作二的话我们每次都会对数组进行排序但是进行的操作并不会保留，因此我们可以利用这个t变量数组先存下一开始的a数组当操作结束之后再把a数组利用t数组还原：

#include
using namespace std;
int n,q;
const int N=10000;
int a[N],t[N];
int main(){
	cin>>n>>q;
	for(int i=1;i<=n;i++){
		cin>>a[i];
	}
	for(int i=1;i<=q;i++){
		int p;
		cin>>p;
		if(p==1){
			int x,v;
			cin>>x>>v;
			a[x]=v;
		}
		else {
			int x;
			cin>>x;
			int m=x;
			for(int j=1;j<=n;j++)
			t[j]=a[j];
			for(int i=2;i<=n;i++){
				for(int j=i;j>=1;j--){
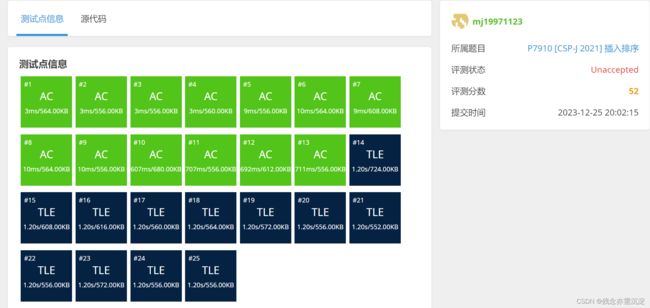
					if(a[j]

but，出题人当然不会这么好心让我用模拟的思路就能直接过掉所有测试点，完完全全的超时了：

最后的结果就是只有五十多分，离满分具有相当大的差距 。

那么接下来就是想一下如何写一个可以获得满分的代码了，当然是运用我们的老伙伴：结构体了，先放代码吧，代码下面我会进行讲解：

#include
using namespace std;
int ans[8100];
int n,Q;
struct number{
	int val,pos;
	bool operator < (const number &A){
		return (val>n>>Q;
       for(int i=1;i<=n;i++){
	       cin>>a[i].val;
	       a[i].pos=i;
	   }
	   for(int i=1;i<=n;i++)
	   {
	   	for(int j=i+1;j<=n;j++)
	   	   if(a[j]>op;
	   	if(op==2){
	   		int x;
	   		cin>>x;
	   		cout<>x>>v;
		   	int p=ans[x];
		   	a[p].val=v;
		   	number tmp=a[p];
		   	for(int j=p;j=2;j--){
			   	if(a[j]

接下来我对这一段代码进行解释：

这段代码定义了一个结构体以及ans数组，结构体里面有两个变量val和pos，分别代表了数字大小以及排名，结构体里面重载了运算符，排序规则就是如果分数不一样就按照从小到大的顺序进行排序，否则就是一开始的序号pos小的排前面，然后把所有需要输入的都输入了之后，将结构体按排序规则进行排序，这里使用的是冒泡排序法，ans数组用于存储原结构体中val的大小顺序，在排序结束后，将它们一开始的排名存储到ans对应的下标中。

接下来就是Q次操作了，从1到Q进行枚举，每次的操作类型是op，如果op为2，直接输出对应的ans，因为排序是我们已经进行过的操作，否则如果是1的话，我们就要将对应x的下标中val改为v，然后利用一个中间变量tmp存下修改后的下标为p的结构体，并将从下标为x的结构体开始，挨着交换到n，然后将n令为tmp再从后到前枚举进行排序以便用于下一步的操作，并将排完序之后的大小顺序利用ans数组来进行更新。

这个思路确实很难想，我想多数的读者和我一样都是想的第一个思想也就是直接模拟，希望读者仔细体会第二段代码，有所收获。

如果读者觉得以上的讲解有用，如果不嫌麻烦的话，希望能得到你的一个赞，万分感谢！