论文浅尝 | 基于属性嵌入的知识图谱实体对齐

论文笔记整理：王中昊，天津大学硕士，方向：自然语言处理。

---

来源：AAAI2019

论文链接： https://doi.org/10.1609/aaai.v33i01.3301297

 

概述

知识图谱之间的实体对齐的任务目标是去找到那些在两个不同的知识图谱上表示现实世界相同的实体。最近，人们提出了基于嵌入的模型应用于实体对齐任务。这种模型建立在知识图谱嵌入模型的基础上，该模型学习实体嵌入以捕获同一知识图谱中实体之间的语义相似性。而作者提议出一种能够学习嵌入进而捕捉不同知识图谱中实体间相似性的模型。这种模型有助于将不同知识图谱中的实体对齐，从而实现多个知识图谱的集成。模型利用知识图谱中存在的大量属性三元组，来生成attribute character embeddings。attribute character embeddings基于它们的属性，将两个知识图谱上的实体嵌入通过计算实体之间的相似度进而转移到同一空间。与此同时，模型也使用传递性规则来进一步丰富实体的属性数目，以增强attribute character embeddings。

 

 

模型和方法

 

模型综述

该模型框架使用基于嵌入的模型，如上图所示。该框架由谓词对齐、嵌入学习和实体对齐三部分模块组成。由于基于嵌入的实体对齐要求两个知识图谱的嵌入（关系和实体嵌入）落在同一向量空间中。为了使关系嵌入有一个统一的向量空间，我们基于谓词相似度（即谓词对齐）合并了两个知识图谱。

谓词对齐模块（后文将详细介绍）将查找部分相似的谓词，例如dbp:bornIn与yago:wasBornIn，并使用统一的命名方案（例如：bornIn）来重命名它们。基于这个统一的命名方案，我们将G1和G2（见上图）合并成为G1_2中。然后，将合并后的图G1_2分为一组关系三元组Tr和一组属性三元组Ta，用于后续的嵌入学习。

嵌入学习模块（后文将详细介绍）利用结构嵌入和属性嵌入共同学习两个知识图谱的实体嵌入。使用上文中生成的关系三元组Tr来进行结构嵌入的学习，而使用属性三元组Ta来进行属性嵌入的学习。最初，来自G1和G2的实体的结构嵌入，由于两个知识图谱中的实体使用不同的命名方案表示，因此落入不同的向量空间。相反的，从属性三元组Ta中学习到的属性嵌入可以落在同一向量空间中。这是通过从属性字符串中学习字符嵌入来实现的，即使属性来自不同的知识图谱（我们称之为attribute character embeddings），也可以是相似的。然后，利用得到的attribute character embeddings将实体的结构嵌入到同一向量空间中，使得实体嵌入能够从两个知识图谱中获取实体间的相似性。例如，假设我们有三元组和来自G1，以及和来自G2。attribute character embeddings允许两个实体lgd:51477和dbp:Germany具有相似的向量表示，因为这两个实体具有相似的属性值“Germany”。然后，实体lgd:240111203和dbp:kromdorf的结构嵌入也将相似，因为这两个实体共享相同的谓词，并且有两个具有相似的向量表示的尾部实体lgd:51477和dbp:Germany，。

一旦我们获得了G1和G2中所有实体的嵌入，实体对齐模块（后文将详细介绍）就会发现每一对，其中h1∈G1和h2∈G2的相似性得分都高于阈值β。为了进一步提高模型的性能，作者所建立的模型使用关系传递性规则来丰富G1和G2中所有实体的属性，进而帮助构建更健壮的属性嵌入以计算实体之间的相似性。

 

1.1 谓词对齐模块

 

谓词对齐模块通过使用统一的命名方案来重命名两个知识图谱中的谓词，从而合并两个KG，以便为关系嵌入提供统一的向量空间。事实上，谓词有命名约定，例如rdfs:label、geo:wgs84pos#lat和geo:wgs84 pos#long。除了命名c约定之外，还有部分匹配的谓词，例如dbp:diedIn vs.yago:diedIn和dbp:bornInvs.yago:wasBornIn。谓词对齐模块找到这些谓词，并使用统一的命名方案（例如：diedIn和：bornIn）重命名它们。为了找到部分匹配的谓词，作者通过计算谓词URI最后一部分的编辑距离（例如bornIn与wasBornIn），并将0.95设为相似度阈值。

 

1.2嵌入学习模块

 

结构嵌入

 

作者将嵌入学习更多地集中在对齐的三元组（即具有对齐谓词的三元组）上，将TransE学习用于知识图谱之间实体对齐的结构嵌入。并且通过添加权重α来控制三元组上的嵌入学习。为了学习结构嵌入，在作者的模型中，最小化了以下目标函数JSE

其中Tr是有效关系三元组的集合，T′r是损坏关系三元组的集合，γ是一个边距超参数，count（r）是关系r的出现次数，|T |是KG合并后，G1_2中三元组的总数。通常，对齐谓词的出现次数高于不对齐谓词，因为对齐谓词同时出现在两个知识图谱中，因此允许模型从对齐的三元组中学习更多内容。

 

属性嵌入

 

就像TransE一样，对于属性字符嵌入，我们将谓词r解释为从头实体h到属性a的翻译。但是，同一个属性a可能以不同的形式出现在两个知识图谱中，例如，50.9989 vs.50.998888889作为实体的纬度；“Barack Obama”vs.“Barack Hussein Obama”作为人名，等等，我们使用复合函数来编码属性值，并将属性三元组中每个元素的关系定义为h+r≈fa（a）。这里，fa（a）是一个复合函数，a是属性值a={c1，c2，c3，…，ct}的字符序列。合成函数将属性值编码为单个向量，并将类似的属性值映射到类似的向量表示。我们定义了三个组合函数如下：

Sum compositional function (SUM)。第一个复合函数定义为属性值的所有字符嵌入的总和：

其中c1、c2、…、ct是属性值的字符嵌入。

 

LSTM-based compositional function (LSTM)。为了解决SUM问题，作者提出了一种基于LSTM的组合函数。此函数使用LSTM网络将字符序列编码为单个矢量。并且使用LSTM网络的最终隐藏状态作为属性值的向量表示：

其中，flstm是由Kimetal定义的LSTM网络（2016年）。

 

N-gram-based compositional function (N-gram)。作者进一步提出了一个基于N-gram的组合函数作为解决SUM问题的替代方法。这里，作者使用属性值的n-gram组合求和。   

其中N表示n-gram组合中使用的n的最大值（在作者的实验中n＝10），t是属性值的长度。

 

为了学习属性字符嵌入，作者将以下目标函数JCE最小化：

其中Ta是来自训练数据集的有效属性三元组，而T′a是损坏属性三元组的集合（a是G中的属性集合）。通过将头实体替换为随机实体或将属性替换为随机属性值，将损坏的三元组用作负样本。要注意的是，这里的f（ta）是基于头部实体h的嵌入、关系r的嵌入和使用合成函数fa（a）计算的属性值的向量表示的似然性得分。

下面要进行结构嵌入与属性字符嵌入的联合学习，作者使用attribute character embedding(hce) ，通过最小化以下目标函数JSIM，将结构嵌入(hse)转移到同一向量空间中：

这里cos（hse，hce）是向量hse和hce的余弦相似性。结构嵌入将基于实体关系捕获两个知识图谱之间实体的相似性，而属性字符嵌入将基于属性值捕获实体的相似性。结构嵌入和属性字符嵌入联合学习的总体目标函数是：

              

 

1.3实体对齐模块

 

由于结构嵌入和属性字符嵌入的联合学习，使得G1和G2的相似实体具有相似的嵌入。因此，生成的嵌入可用于实体对齐。我们计算下列实体对齐方程：

给定一个实体h1∈G1，我们计算h1与所有实体h2∈G2之间的相似性。是预期的对齐实体对。我们使用相似性阈值β来过滤太不相似而无法对齐的成对实体。

 

 

1.4通过传递性规则丰富三元组

 

尽管嵌入的结构隐式地学习了关系传递信息，但是显式地包含这些信息会增加每个实体的属性和相关实体的数量，这有助于识别实体之间的相似性。例如，给定三元组和,我们可以推断dbp:EmporiumTower与dbp:England有关系（即“：locatedInCountry”）。实际上，这些信息可以用来丰富相关实体dbp:Emporium Tower。作者将一跳传递关系处理如下，给定传递三元组和，我们将r1.r2解释为从头实体h1到尾实体t2的关系。因此，这些传递三元组之间的关系被定义为h1+（r1.r2）≈t2。通过用r1.r2代替关系向量r，也增强了上文提到的嵌入模型的最小化目标函数。

实验

作者在四个真实的KG上评估了他们的模型，包括DBpedia（DBP）（Lehmann等人。2015年），LinkedGeoData（LGD）（Stadler等人。2012年），Geonames（GEO）2和YAGO（Hoffart等人。2013年）。作者使用提出的模型，将DBP的实体分别与LGD、GEO和YAGO的实体对齐。将模型发现的对齐实体与三个地面真值数据集（DBP-LGD、DBP-GEO和DBP-YAGO）中的对齐实体进行比较，这三个数据集分别包含了DBP和LGD、GEO和YAGO之间的对齐实体。

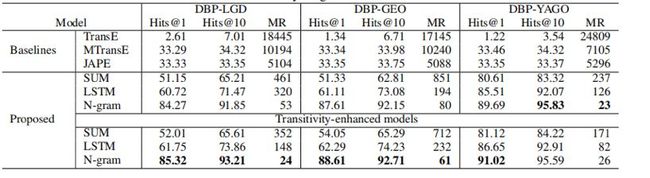
作者使用hits@k（k=1，10）（即正确对齐的实体在前k个预测中所占的比例）和正确（即匹配）实体的排名的平均值来评估模型的性能。较高的hits@k和较低的MR表明该模型的性能更好。对于来自DBP的每个实体，作者使用公式计算与来自另一个KG（LGD/GEO/YAGO）的实体的相似性得分。如表1所示，作者提出的模型始终优于基线模型，基于MR的t检验，p<0.01。同时，MTransE和JAPE依赖于种子排列的数量（作者使用黄金标准的30%作为原始文件中建议的种子排列）。

表1

 

在作者的attribute character embedding模型中，使用N-gram复合函数比使用LSTM或和复合函数获得了更好的性能，因为N-gram复合函数在将属性字符串映射到其向量表示时比其他函数更好地保持字符串的相似性。同时由于传递性规则丰富了实体的属性，进而更好地提高了模型的性能。为了评估属性字符嵌入在捕获实体间相似性方面的能力，作者进一步创建了基于规则的实体对齐模型，其中只使用实体标签字符串之间的编辑距离以对齐实体。对于DBP-LGD和DBP-GEO数据集，作者添加坐标相似性作为额外的度量，因为这两个数据集只包含位置实体。从表2可以看出，作者的模型的嵌入结果可以作为一个附加特性添加，以增强基于规则的模型的性能。

表2

 

总结

针对知识图之间的实体对齐问题，作者提出了一种实体结构嵌入与属性字符嵌入相结合的嵌入模型。模型使用属性字符嵌入将实体嵌入从不同的知识图谱转移到相同的向量空间。此外，作者采用传递性规则来丰富实体的属性数目，以帮助识别基于属性嵌入的实体之间的相似性。作者提出的模型在三对真实世界知识图谱之间的实体对齐方面的hits@1始终超过基准50%。

 

---

 

OpenKG

开放知识图谱（简称 OpenKG）旨在促进中文知识图谱数据的开放与互联，促进知识图谱和语义技术的普及和广泛应用。

点击阅读原文，进入 OpenKG 博客。