数学建模|通过模拟退火算法求解供货与选址问题：问题二（python代码实现）

今天继续用模拟退火算法供货与选址问题的问题二，如果还没看过问题一的可以看我之前的博客

数学建模|通过模拟退火算法求解供应与选址问题：问题一（python代码实现）-CSDN博客

这里还是把题目放上来（题目来自数学建模老哥的视频）：

那么我们可以分析一下，第一问和第二问还是有联系的。区别就是第一问的A和B的坐标是固定的，所有AB到六个工地的距离也是固定的，我们的自变量就是AB对六个工地的供货量。这个自变量的解，我们在第一问已经求出来了。第二问这里，AB的坐标就不固定了。也就是AB坐标也成了我们要求的自变量的一部分。那我们的自变量就变成了 AB的坐标 + AB的供货量。因为我们的目标函数 = 距离 × 供货量，第一问的距离是固定的，所有我们不用管它。但是第二问，AB的坐标在变化，所有我们每次计算目标函数的时候都要重新计算一次距离。那么我们就要写一个计算距离的函数，就叫get_juli()吧。那么我们这个距离函数要怎么才能计算距离，是不是要先从自变量里拿到我们AB当前的坐标，才能计算距离并返回，那它的计算方式还是和第一问一样。

分析到这里其实就差不多，与第一问相比就多了一个AB的坐标和一个距离函数。其他都和第一问差不多。

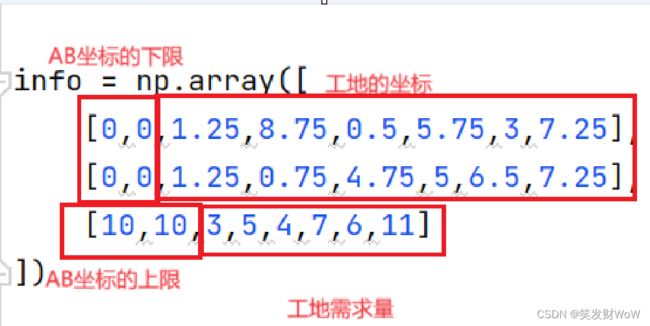
这里先用一个numpy数组存储我们的自变量，也就是AB的坐标和AB的供货量。

这里用一个两行八列的数组存储就行了，每个元素代表什么意思我也写清楚了。

我们再用一个info数组存储一些固定信息，包括工地的坐标和需求量，AB坐标的取值范围。方便我们计算的时候直接获取到。这里再说一下，为什么AB坐标的变化范围是0到10呢？当然是猜的啦。因为工地坐标的变化范围也是在0到10之间。如果把AB坐标的变化范围搞得很大，就会多出很多无效计算。

然后我们定义我们距离函数，这个函数要把自变量传进去，然后获取到AB当前的坐标，再与info中的工地坐标进行计算就能得到距离了，公式和第一问是一样的。

def get_juli(x):
    juli = np.array([
        np.sqrt(np.sum((info[0:2,2:9] - x[0:2,0:1]) ** 2, axis=0)),
        np.sqrt(np.sum((info[0:2,2:9] - x[0:2,1:2]) ** 2, axis=0))
    ])
    return juli

然后，再定义目标函数和约束条件，这里和第一问是一样的。不过要注意，因为自变量x与第一问的自变量有一点点改变，所有我们要保证约束条件接收到的是AB的供货量而不包括AB的坐标。

target_fun = lambda x,juli: np.sum(juli * x[0:2,2:9])
st_fun1 = lambda x: np.sum(x[0:2,2:9],axis=1)[0]<=20 and np.sum(x[0:2,2:9],axis=1)[1]<=20
st_fun2 = lambda x ,info: np.all(np.sum(x[0:2,2:9],axis=0) == info[2][2:9], axis=0)
judgy_st = lambda x,info:st_fun1(x) and st_fun2(x,info)

再就是设计自变量的更新方式。大体和第一问是一样的，就是多了AB坐标的更新方式。那就多写一个判断语句，如果更新的是AB的坐标就随机给坐标一个数就行了（包括整数和浮点数）。

def get_x(x,lb,t_move):
    i = random.randint(0,1)
    j = random.randint(0,7)
    ub = info[2][j] #这里取的是x的上限
    lb = x[i][j]-t_move*(x[i][j]-lb)
    ub = x[i][j]+t_move*(ub-x[i][j])
    # print(t_move)
    #如果是更新AB的坐标，就这样操作
    if j == 0 or j == 1:
        if random.random() > random.random():
            x[i][j] = random.uniform(lb,ub)
        else:
            x[i][j] = random.randint(lb,ub)
        return x

    #如果是更新AB的供货量，就这样操作
    if random.random() > random.random():
        x[i][j] = random.randint(int(lb), int(ub))
        x[(i + 1) % 2][j] = ub - x[i][j]
    else:
        x[i][j] = random.uniform(lb,ub)
        x[(i+1) % 2][j] = ub-x[i][j]
    return x

现在万事俱备，就是带入模拟退火算法，计算了。直接上代码：

#%%
import random
import numpy as np
import math

t = 200000000
T = 200000000
dt = 0.999999993
eps = 1e-14
n = 0


info = np.array([
    [0,0,1.25,8.75,0.5,5.75,3,7.25],
    [0,0,1.25,0.75,4.75,5,6.5,7.25],
    [10,10,3,5,4,7,6,11]
])

x = np.zeros([2,8])
#%%
def get_juli(x):
    juli = np.array([
        np.sqrt(np.sum((info[0:2,2:9] - x[0:2,0:1]) ** 2, axis=0)),
        np.sqrt(np.sum((info[0:2,2:9] - x[0:2,1:2]) ** 2, axis=0))
    ])
    return juli

#%%
target_fun = lambda x,juli: np.sum(juli * x[0:2,2:9])
st_fun1 = lambda x: np.sum(x[0:2,2:9],axis=1)[0]<=20 and np.sum(x[0:2,2:9],axis=1)[1]<=20
st_fun2 = lambda x ,info: np.all(np.sum(x[0:2,2:9],axis=0) == info[2][2:9], axis=0)
judgy_st = lambda x,info:st_fun1(x) and st_fun2(x,info)

#%%
def get_x(x,lb,t_move):
    i = random.randint(0,1)
    j = random.randint(0,7)
    ub = info[2][j]
    lb = x[i][j]-t_move*(x[i][j]-lb)
    ub = x[i][j]+t_move*(ub-x[i][j])
    # print(t_move)
    #如果是更新AB的坐标，就这样操作
    if j == 0 or j == 1:
        if random.random() > random.random():
            x[i][j] = random.uniform(lb,ub)
        else:
            x[i][j] = random.randint(lb,ub)
        return x

    #如果是更新AB的供货量，就这样操作
    if random.random() > random.random():
        x[i][j] = random.randint(int(lb), int(ub))
        x[(i + 1) % 2][j] = ub - x[i][j]
    else:
        x[i][j] = random.uniform(lb,ub)
        x[(i+1) % 2][j] = ub-x[i][j]
    return x


#%%
move = 11
jud_n = 0
best_x = get_x(x,0,1)
# breakpoint()
while judgy_st(best_x,info) != True:
    best_x = get_x(best_x,0,1)
    jud_n += 1
best_y = target_fun(best_x,get_juli(x))
print(f"f = {best_y},x = {best_x},第{jud_n}次循环")
y = best_y

#%%
while n!= 200000 :
    # print(t/T)
    dx = get_x(x,0,1)
    judgy_n = 0
    while judgy_st(dx,info) != True:
        dx = get_x(dx,0,1)
        judgy_n += 1
        if judgy_n == 1000000:
            break
    if judgy_n == 1000000:
        continue
    dy = target_fun(dx,get_juli(dx))

    if dy < y:
        y = dy
        x = dx
        if dy < best_y:
            best_y = dy
            best_x = dx
            print(f"f = {best_y},\n x = \n{best_x}\n第{n}次循环")

    elif  np.exp((y - dy) / t)  > random.random():
        y = dy
        x = dx

    # print(f"f = {y},x = {x},第{n}次循环")

    t = t * dt
    n += 1

print(n)

看一下结果：

然后是，视频给出来到解：

可以看到我们计算出的解，比视频的解还节省的10的吨千米数，那我们的计算结果是更优的。然后就是为什么计算的结果会和视频的不一样。这点也不用纠结，因为视频里他计算的结果也不是每次都一样的。只要结果有说服力就行了。