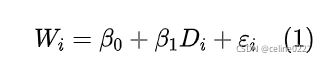PSM倾向得分匹配
1. 简要介绍
我们以 是否上大学 (
) 对 收入 (
) 的影响为例来说明这个问题。这里，先讲二者的关系设定为如下线性模型：
显然，在模型 (1) 的设定中，我们可能忽略了一些同时影响「解释变量」—— 是否上大学 () 和「被解释变量」—— 收入 () 的因素，例如，家庭背景、能力、动机、个人兴趣等。这些因素被称为「共同因素 (Common Factors)」，因为他们同时影响被解释变量和解释变量，但又往往不可观测或无法获取数据。
从计量经济学的角度来讲，在模型设定中遗漏的「共同因素」都会「跑到」干扰项 
中。由于这些被遗漏的「共同因素」往往与 相关，也就自然导致
，从而导致 
估计可能是有偏的。为了解决这个问题，可以通过多元回归 (MR) 解决，见式 (2):
假设，智商 (
) 是影响是否上大学和收入的唯一因素，则式 (2) 可以无偏的估计 。看似正确，但最大问题是 W 和 X 的线性关系并不总是成立。函数形式的错误设定 (FFM) 被误差项 () 吸收，使得 与 相关， 有偏。
匹配是解决 FFM 问题的一种方法。通过为上大学的人 (=1) 匹配智商 () 相近的未上大学的人 (=0)，弱化对函数形式设定的依赖，缓解函数形式错误设定 (FFM) 导致的内生性问题。当然，匹配更多是根据多个变量 (
) 计算的概率进行匹配，且 同时影响 和 ，概率值计算见式 (3)：
实际上，匹配也有一定局限性。若智商 () 对是否上大学 () 有较强的预测能力，匹配后的样本更有可能会排除高(低) 上大学(不上大学)的个体。换言之， 对 预测能力越强，匹配的样本越少，质量也就越差。
假设条件
A. 共同支撑假设（common support）
共同支撑假设要求处理组和控制组样本特征分布有一定的重叠以保证匹配质量。即需要满足pscore[处理组]min<=pscore<=pscore[控制组]max 。
B. 平行假设（balancing）
平行假设要求匹配过后的处理组和控制组偏差（bias）在5%以下 ，或者是T-test检验结果显示匹配过后的处理组和控制组无显著差异。
2. 错误理解和局限性
PSM 在减少处理变量和可观测变量相关性方面发挥着重要的作用，PSM 是通过控制与被解释变量和处理变量相关的可观测变量来缓解选择偏差，但有局限性：
（1）PSM 并不能解决由「选择偏差或遗漏变量」所导致的内生性问题。
PSM 只是通过匹配的方式在一定程度上避免了 FFM 导致的偏差，并没有从根本上解决由「选择偏差或遗漏变量」所导致的内生性问题。
（2） PSM 不能被称为「准实验」，也无法模拟实验条件。
尽管处理组和对照组的协变量平衡可能类似于实验条件，PSM 仍缺少实验的重要特征。
首先，PSM 只是缓解了可观测变量的系统差异，不可观察变量的差异并未缓解。而实验通过随机分配，可以有效控制可观测和不可观察变量影响。其次，PSM 决定了哪些观测值进入分析的样本中。
（3）PSM 的外部有效性问题。
PSM 的另一个问题是与外部有效性有关。在「共同支撑假设 (Common Support)」无法满足或很牵强的情况下，PSM 会系统排除缺乏对照组的样本，进而使得样本代表性变差，影响结果的外部有效性。
3. 主要设计选择
在实践中，PSM 需要多种设计选择。即使样本和协变量不变，不同的设计选择仍可能得出不同的结论。
A. 估计倾向得分的主要设计选择：
-
处理组和控制组的识别。若处理变量为二分变量，则处理组合控制组可以直接识别。若处理变量为连续变量，则需要指定分界点识别处理组和控制组。后者，更容易将匹配样本限定在分界点附近，这就降低了检验的显著性，增加了犯第二类错误的概率。
-
预测模型设计。一个常见的错误理解，PSM 预测模型变量的选择应该使预测能力最好。实际上，由于 PSM 主要是解决 MR 模型错误设定导致的偏差，PSM 和 MR 变量的选择上应该保持一致性，如果理论不支持一个变量包含在 MR 模型中，那么也不应该包含在 PSM 模型中，否则就不可避免的受事后选择的质疑。
B. 形成匹配样本的主要设计选择：
-
重复和不可重复匹配。不可重复匹配使得每个控制组只能匹配一次，即使该控制组是多个处理组的最佳匹配，这就使得匹配质量降低和样本变小。相反，重复匹配则可以有效避免这些问题，但是在估计处理效应时，需进行加权和调整标准误，以反映匹配次数的影响。当然，也要注意极端控制组被重复匹配多次对推断结果的影响。
-
匹配半径的设定。设定一个相对严格的「半径」值一般可以有效避免「糟糕」的匹配和提高协变量的平衡性。
-
「1 对 1」 和「1 对多」匹配。会计研究中最常见的匹配方法是 1:1 匹配，但是在存在多个合理匹配样本时，「一对多」匹配可以降低抽样方差。与重复匹配一样，在「一对多」匹配时，也需要考虑加权。
B. 形成匹配样本的主要设计选择：
-
重复和不可重复匹配。不可重复匹配使得每个控制组只能匹配一次，即使该控制组是多个处理组的最佳匹配，这就使得匹配质量降低和样本变小。相反，重复匹配则可以有效避免这些问题，但是在估计处理效应时，需进行加权和调整标准误，以反映匹配次数的影响。当然，也要注意极端控制组被重复匹配多次对推断结果的影响。
-
匹配半径的设定。设定一个相对严格的「半径」值一般可以有效避免「糟糕」的匹配和提高协变量的平衡性。
-
「1 对 1」 和「1 对多」匹配。会计研究中最常见的匹配方法是 1:1 匹配，但是在存在多个合理匹配样本时，「一对多」匹配可以降低抽样方差。与重复匹配一样，在「一对多」匹配时，也需要考虑加权。
C. 评估匹配样本：
-
一般通过对处理组和控制组协变量均值或中位数差异检验来评价匹配效果。但是，考虑到匹配后样本减少，犯第二类错误概率增加，差异不显著并不能说明匹配后样本可以有效免 FFM 问题。另一方面，协变量差异显著，而在数值上也可能比未匹配样本小的多，也可以避免 FFM 问题。
D. 匹配方法：
-
k近邻匹配（k-Nearest neighbors matching），即寻找倾向得分最近的k个不同组个体。其中k=1则为一对一匹配（One-to-one matching）
-
卡尺匹配（Caliper matching）或半径匹配（Radius matching），即限定某个绝对距离值进行倾向得分匹配
-
核匹配（Kernel matching），通过指定带宽h带入核函数计算权重进行匹配
-
局部线性回归匹配（Local linear regression matching），通过局部线性回归来估计权重进行匹配
-
样条匹配（Spline matching），使用“三次样条”来估计权重进行匹配
在实际进行匹配时，我们应根据具体数据的样本量，数据性质等选择匹配方法，并可尝试同时使用不同的匹配方法对实证结果进行检验。
E. 匹配变量的选择
-
选择协变量，尽量将可能影响（Y0i,Y1i)（结果变量）和Di（处理变量）的相关变量包括进来，如果协变量选择不当或太少，导致可忽略性假设（不存在任何与解释变量相关的遗漏变量）不满足将引起偏差。
F. 估计处理效应：
-
样本匹配后，处理效应可以通过简单的 t 检验或者 MR 进行估计。如果协变量实现了真正的平衡，那么简单的 t 检验是可以的。然而，研究者不能接受协变量平衡的零假设，因此推荐使用 MR 来调整协变量剩余的差异。
4. PSM的局限性
- PSM 不能被称为 “准实验”，也无法模拟实验条件
- PSM通常要求比较大的样本容量以得到高质量的匹配
- PSM要求处理组与控制组的倾向得分有较大的共同取值范围；否则，将丢失较多的观测值，导致剩下的样本不具有代表性
- PSM只控制了可测变量的影响，并没有从根本上解决由选择偏差或遗漏变量导致的内生性问题，更不能代替 Heckman 和 IV 等方法用于解决自选择、遗漏变量等问题
5. Stata操作
首先判断简化模型和拓展模型之间系统显著性差异
扩展模型是在简化模型的基础上，加入所有控制变量的二次项和三次项。 Chow 检验显著，说明这里存在 FFM 问题。
-定义全局暂元
global indepvar LNASSET LEV ROA GROWTH BM AGE
global fixvar i.indcode i.year
*-样本匹配
probit BIG4 $indepvar $fixvar, vce(cluster stkcd)
est store Probit
predict pscore, p
psmatch2 BIG4, pscore(pscore) outcome(ABSACC RESTATE) ///
common n(1) norepl cal(0.03) //详见help文件
pstest $indepvar, both graph
psgraph
*-回归结果
*-Full Sample ABSACC
reg ABSACC BIG4 $indepvar $fixvar, cluster(stkcd)
est store ABSACC_F
*-Matched Sample ABSACC
reg ABSACC BIG4 $indepvar $fixvar [fweight=_weight], cluster(stkcd)
est store ABSACC_M
*-Full Sample RESTATE
reg RESTATE BIG4 $indepvar $fixvar, cluster(stkcd)
est store RESTATE_F
*-Matched Sample RESTATE
reg RESTATE BIG4 $indepvar $fixvar [fweight=_weight], cluster(stkcd)
est store RESTATE_M
*-结果对比
local m "Probit ABSACC_F ABSACC_M RESTATE_F RESTATE_M"
esttab `m', mtitle(`m') b(%6.3f) nogap drop(*.indcode *.year) ///
order(BIG4) s(N r2_p r2_a) star(* 0.1 ** 0.05 *** 0.01) 使用 psmatch2 命令后，会自动生成「_weight」变量。该变量代表匹配次数，在 1:1 非重复匹配下，_weight != . 表示匹配成功，且匹配成功时 _weight = 1。在 1:1 可重复匹配下，参与匹配的控制组 _weight 的取值可能为任意整数。
一旦获得了 _weight 变量，就相当于对样本的匹配情况进行了标记，我们可以直接在 regress 命令后附加加 fweight = _weight 进行样本匹配后的回归。其中，fweight 为「frequency weights」的简写，是指观测值重复次数的权重。若是 1:2 重复匹配，成功匹配的处理组 _weight = 2 / 2，成功匹配的控制组 _weight = 参与匹配次数 / 2，即都要除以 2 进行标准化。因此，若想继续使用 fweight 选项，需要 _weight * 2 转化为频数。详细请参考 Propensity Score Matching in Stata using teffects、[psmatch2 and fweight option of regress]。
结果介绍
第一个表列示了匹配前和匹配后处理组和控制组差异及其显著性，以 ABSACC 为例，匹配前处理组和控制组差异为「-.011637968」，并且 t 值为「-6.02」，匹配后处理组和控制组差异「ATT」为「-.006573884」，并且 t 值为「-2.47」。
在第一个表中，Note 显示所汇报的标准误未考虑倾向得分估计的事实 (即假设倾向得分为真实值，然后推导标准误)，详情参见：Propensity Score Matching in Stata using teffects。实际上，这里仅对系数的标准误和显著性有影响，而对系数值并不产生影响，也不会对匹配结果产生影响
第二个表列示了处理组合控制组在共同取值范围的情况，其中控制组「17,726」个样本都在共同取值范围内，而处理组有「184」个样本不在共同取值范围内，有「1,163」在共同取值范围内。
pstest 命令主要考察匹配质量，以检验是否满足「平衡性假设 (balancing assumption)」。从下表可以看出，匹配后大多数变量标准化偏差 (%bias) 都比较小，而且 t 值都不拒绝处理组和控制组无系统性偏差的原假设。从下图也可以看出，所有变量的标准差在匹配后都缩小了。
6. 使用建议
-
应该将 PSM 作为解决 FFM 问题的一种方法，而不是更广泛的内生性、自选择、以及遗漏变量的问题。
-
在使用过程中，应该将 PSM 和 MR 结合对比使用。同时，要对单一 PSM 样本结论保持谨慎态度。
-
PSM 第一阶段不应该包含 MR 模型排除的变量。在 PSM 模型第二阶段应使用所有控制变量进行 MR 回归 (doubly robust estimation)。
-
应披露 PSM 的设计选择，提高研究的可复制下和清晰度。具体来看，PSM 第一阶段模型、PSM 第二阶段模型、是否可重复匹配、多少个对照组样本匹配一个处理组样本、匹配半径 (如实施)、以及匹配质量 (协变量平衡性)。
逐年匹配
encode industry,gen(hangye)
global psm_var "Size Leverage OCF CAPX NWC Growth Largest SIGMA Div MB_1 hangye"
//通常行业匹配用19位代码
bysort year: egen quart_ew75=pctile(Ln_geodistance_ew), p(75)
gen distance_ew_high=(Ln_geodistance_ew>quart_ew75) if Ln_geodistance_ew!=.
forvalue i = 2007(1)2019{
preserve
keep if year == `i' //esc下的波浪号和单引号
set seed 0001
gen tmp = runiform()
sort tmp
psmatch2 distance_ew_high $control, out(ln_Cash_ratio1) logit ate neighbor(2) ties //noreplacement
//drop if _weight ==.
cap save `i'.dta,replace // cap表示有没有报错都继续执行
restore
}
use 2007.dta,clear
forvalues i =2007(1)2019{
cap append using `i'.dta
}
duplicates drop stkcd year,force
drop if _weight ==.
save 2007_2019_PSM.dta, replace
//在新数据上回归
xi:reg ln_Cash_ratio1 Ln_geodistance_ew $control i.year i.industry2
outreg2 using Table4B,excel drop(_I*) dec(3) tdec(3) bdec(3) alpha(0.01,0.05,0.1) symbol(***,**,*) stats(coef tstat) e(r2_a)
pstest $psm_var,both graph
teffects psmatch (y) (t x1 x2, probit), atet nn(#) caliper(#)
不选probit就默认logit, atet是显示ate on the treated, nn(#)里面的#表示1对#匹配，caliper表示卡尺内匹配#表示水平。teffects psmatcgh比之前的psmatch2的优点是提供了Abadie & Imbens(2012)的稳健标准误，其他的差不多。