代码随想录算法训练营第五天| 哈希表 242. 有效的字母异位词 349. 两个数组的交集 202. 快乐数 1. 两数之和
哈希表基本知识
哈希表中关键码就是数组的索引下标,然后通过下标直接访问数组中的元素,哈希表的作用是用来快速判断一个元素是否出现集合里。在查询时,枚举的时间复杂度是O(n),但如果使用哈希表的话, 只需要O(1)就可以做到。
但是哈希法也是牺牲了空间换取了时间,因为我们要使用额外的数组,set或者是map来存放数据,才能实现快速的查找。
如果在做面试题目的时候遇到需要判断一个元素是否出现过的场景也应该第一时间想到哈希法!
如果数量大于哈希表的大小怎么办,此时就算哈希函数计算的再均匀,也避免不了会有重复的名字同时映射到哈希表 同一个索引下标的位置。
哈希碰撞
两不同名值都映射到相同索引位置的过程称为哈希碰撞。解决哈希碰撞的方法有拉链法和线性探测法。
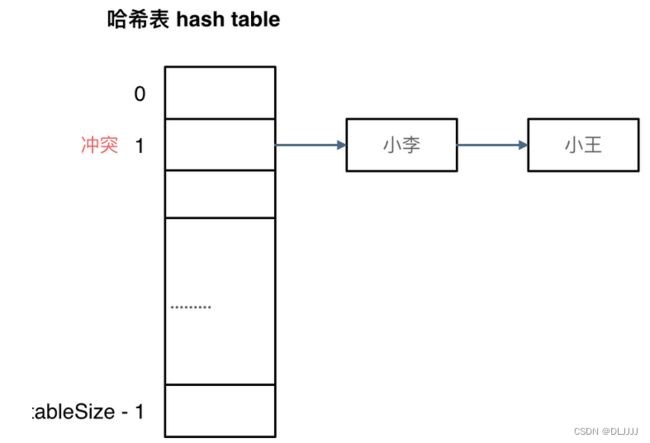
拉链法
在索引的位置发生了冲突时,发生冲突的元素都被存储在链表中。 这样我们就可以通过索引找到元素
(数据规模是dataSize, 哈希表的大小为tableSize)
其实拉链法就是要选择适当的哈希表的大小,这样既不会因为数组空值而浪费大量内存,也不会因为链表太长而在查找上浪费太多时间。
线性探测法
使用线性探测法,一定要保证tableSize大于dataSize。 我们需要依靠哈希表中的空位来解决碰撞问题。
冲突的位置,放了其中一个元素,那么就向下找一个空位放置另一冲突元素的信息。
常见的三种哈希结构
使用哈希法来解决问题的时候,一般会选择如下三种数据结构。数组、集合、映射
在C++中,set 和 map 分别提供以下三种数据结构,其底层实现以及优劣如下表所示:
集合
| 集合 | 底层实现 | 是否有序 | 数值是否可以重复 | 能否更改数值 | 查询效率 | 增删效率 |
|---|---|---|---|---|---|---|
| std::set | 红黑树 | 有序 | 否 | 否 | O(log n) | O(log n) |
| std::multiset | 红黑树 | 有序 | 是 | 否 | O(logn) | O(logn) |
| std::unordered_set | 哈希表 | 无序 | 否 | 否 | O(1) | O(1) |
std::unordered_set底层实现为哈希表,std::set 和std::multiset 的底层实现是红黑树,红黑树是一种平衡二叉搜索树,所以key值是有序的,但key不可以修改,改动key值会导致整棵树的错乱,所以只能删除和增加。unordered_set在C++11的时候被引入标准库
映射
| 映射 | 底层实现 | 是否有序 | 数值是否可以重复 | 能否更改数值 | 查询效率 | 增删效率 |
|---|---|---|---|---|---|---|
| std::map | 红黑树 | key有序 | key不可重复 | key不可修改 | O(logn) | O(logn) |
| std::multimap | 红黑树 | key有序 | key可重复 | key不可修改 | O(log n) | O(log n) |
| std::unordered_map | 哈希表 | key无序 | key不可重复 | key不可修改 | O(1) | O(1) |
std::unordered_map 底层实现为哈希表,std::map 和std::multimap 的底层实现是红黑树。同理,std::map 和std::multimap 的key也是有序的(这个问题也经常作为面试题,考察对语言容器底层的理解)。
当我们要使用集合来解决哈希问题的时候,优先使用unordered_set,因为它的查询和增删效率是最优的,如果需要集合是有序的,那么就用set,如果要求不仅有序还要有重复数据的话,那么就用multiset。在map 是一个key value 的数据结构,map中,对key是有限制,对value没有限制的,因为key的存储方式使用红黑树实现的。虽然std::set、std::multiset 的底层实现是红黑树,不是哈希表,std::set、std::multiset 使用红黑树来索引和存储,不过给我们的使用方式,还是哈希法的使用方式,即key和value。所以使用这些数据结构来解决映射问题的方法,我们依然称之为哈希法。
242. 有效的字母异位词
本题参考哈希表的思路,使用数组映射。由于本题是对字符串操作且只有小写字符,可以定义一个长度为26的数组,统计题中一个字符串中各字符出现的次数,然后针对另外一个字符串,如果出现了一字符,在前面的统计结果那里-1。完成遍历后,判断结果那个数组是否全为0,是的话表示有效的字母异位词。
class Solution {
public:
bool isAnagram(string s, string t) {
int a[26]{0};
for(int i=0;i349. 两个数组的交集
与上一题想对比,题目中,nums的取值可以为0~1000,可以使用第一题的思想完成,但是当nums的取值逐渐变大,或者nums的数值分布较为稀疏,使用数组申请的内存过大,会导致内存浪费,可以使用集合来代替。由于本题中只需要找到相交的元素,不需要找到相交元素的个数,使用unordered_set即可。首先将其中一串数组导入设置的unordered_set中,遍历数组2,如果数组2中的元素在前面的哈希集合中能够找到,将结果插入前面定义的hash集合中,不直接定义函数返回值vector的原因是便于去重。
class Solution {
public:
vector intersection(vector& nums1, vector& nums2) {
unordered_set hash;
unordered_set num1(nums1.begin(),nums1.end());
for(int i=0;i(hash.begin(), hash.end());
}
}; 202. 快乐数
本题的思想为如果在获得平方和的过程中找到两个相同的数,那么会一直循环下去,因此,找到两相同的平方和便可以停止了。因此,本题也可以使用之前环形链表的思想,设置快慢指针然后再判断。前面有一个关键词——找到,快速查找应该第一时间想到哈希,因此使用哈希的解法如下
class Solution {
public:
int sumnum(int n){
int sum{0};
while(n){
sum +=( n % 10 )* (n % 10);
n/=10;
}
return sum;
}
bool isHappy(int n){
unordered_set hash;
while(1){
int num=sumnum(n);
n=num;
if(num==1)return 1;
if(hash.find(num)!=hash.end()){
return 0;
}else{
hash.insert(num);
}
}
}
}; 1. 两数之和
可以使用暴力解法,即两层循环然后返回,同时,本题也可以使用哈希法,首先找到一个元素,然后求出目标值与该元素的差值,在哈希表中查找,如果找到说明可以返回,如果没有找到就得继续找,把该元素的值和下标都放入哈希表中,所以得用map。然后还要注意,由于需要按照key搜索,需要将下标存在value,找到的下标中,指针的second一定是在前面的,因为后面才会搜索到前面插入map的数值
class Solution {
public:
vector twoSum(vector& nums, int target) {
unordered_map hash;
for(int i=0;i::iterator it=hash.find(target-nums[i]);
if(it!=hash.end()){
return {it->second,i};
}
hash.insert(pair (nums[i],i));
}
return{-1,-1};
}
};