李宏毅机器学习第一周_初识机器学习

目录

摘要

一、机器学习基本概念

1、Machine Learning≈Looking for Function

2、认识一些专有名词

二、预测YouTube某天的浏览量

一、利用Linear model

二、定义更复杂的函数表达式

三、ReLU函数

四、Sigmoid函数与ReLU函数的对比

三、反向传播(Backpropagation)

一、反向传播的基本思想(正向计算-误差计算-梯度计算-参数更新)

二、计算过程

总结

---

摘要

在本周的学习中，学习了机器学习的一些基本概念以及术语；然后利用预测YouTube浏览量这一个例子，学会了如何去定义一个model，如何定义Loss，如何去调整参数；还学会了利用反向传播来更新参数。

一、机器学习基本概念

1、Machine Learning≈Looking for Function

即机器学习就是帮助人们找到一个人类写不出来的函式。不同的输入可以通过函式的处理可以得到不同的输出 。

2、认识一些专有名词

(1)Regression:The function outputs a scalar.（输出是一个数值）

 (2)Classification:Given options(classes)，the function outputs the correct one.(给出一些选项，然后这个函式的任务就是从这些选项中选出正确的结果)

 如Playing Go便是从19*19的棋盘中，给棋子选出一个正确位置。

二、预测YouTube某天的浏览量

一共分为三个步骤：(1)写出一个带有位置参数的函数表达式(2)从训练数据中定义LOSS(3)对参数进行优化。具体步骤如下所示：

一、利用Linear model

Step1：定义一个带有未知参数的函数表达式

 首先定义了一个线性模型,其中b与w是未知参数，y是要预测的某一天的浏览量，x是前一天已知的浏览量，我们需要做的就是去找到合适的b与w，使得此模型能够较为精准地预测出第二天的浏览量。

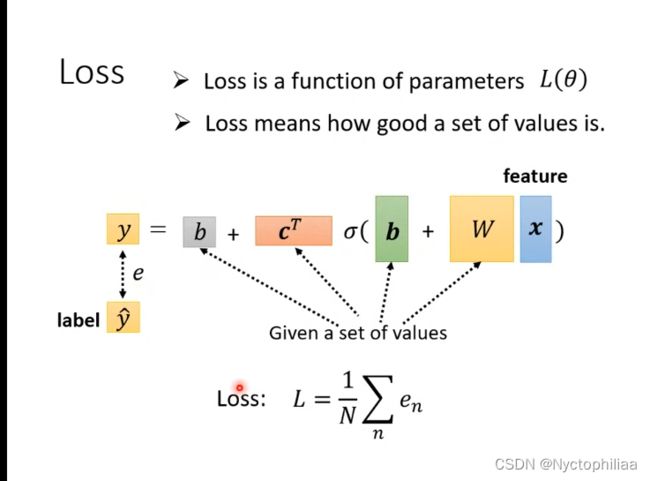
Step2：从训练数据上定义LOSS

  LOSS也是一个function，它的输入就是未知参数w与b，它的输出就是根据输入的未知参数的值，来得到这组输入的值是好还是不好。这个损失值LOSS越大，证明b和w选择的越不好；而损失值LOSS越小，证明这一组参数b和w选择的越好

Step3:优化参数

若函数L只有一个未知参数w，它与w的函数图像如图所示，那么优化参数其实就是一个求偏导数的过程，给自变量w定义一个初始值 ,计算L对w在该点处的偏导数，再用        得到新的参数值，然后不断调整w的值(调整原则：如果偏导数的值是正的，则减小w的值；若偏导数的值是负的，则需要增大w的值 ),至到偏导数在某一点的值为0停止。其中是一个超参数

注：最终得到的w是Local Minima，而不一定是global Minima

同理，若未知参数是两个，调整步骤相同。

当然，我们不止可以利用前一天的浏览量来预测当天的浏览量，这样做有很大的局限性，我们也可以使用前3天或7的浏览量当作一个循环，把这些天的浏览量都考虑进来。

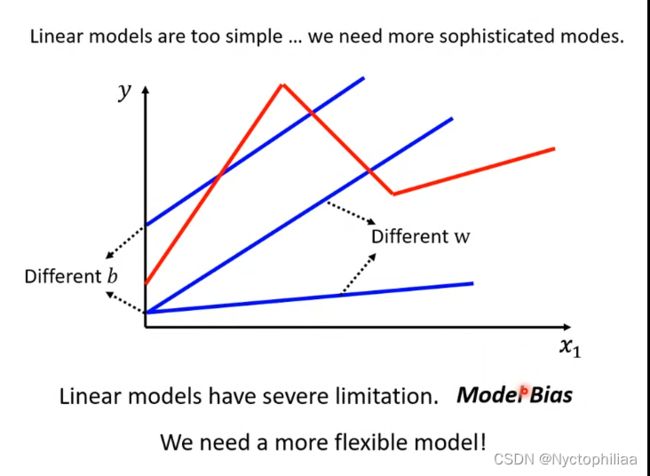
二、定义更复杂的函数表达式

比如说，如果浏览量曲线如下图所示：

 那么如果只是用linear model肯定不能进行准确的预测，所以我们需要用更复杂的function。比如说：sigmoid函数或者ReLU函数。

所以我们就可以得到新的模型：

 

用此模型来预测浏览量的步骤与使用线性模型来预测浏览量的步骤类似。具体步骤如下：

(1) 

 (2)其中向量由一些列未知参数组成。

(3)优化

注：目标函数都比较复杂，为了问题的简化，我们一般将目标函数在某点邻域展开成泰勒多项式来逼近原函数，计算过程如下：

通过这样不断迭代的值，使得函数值不断下降，从而达到优化参数的目的。

三、ReLU函数

ReLU函数是深度学习中最重要和最常用的激活函数之一。它的定义是:f(x) = max(0, x)，其中x是输入信号。从表达式可以看出，ReLU函数当x < 0时,f(x) = 0；当x >= 0时,f(x) = x。其输出范围是(0, +∞)

 其中ReLU中的2i是因为2个ReLU函数才能合成一个Sigmoid函数

四、Sigmoid函数与ReLU函数的对比

1.表达式不同

sigmoid函数表达式：;ReLU函数表达式:max(0,x)

2.输出值的范围不同

sigmoid函数的值域是(0,1);而ReLU函数的值域是(0,+∞)

3.导数特性不同

sigmoid函数的导数图像是先增后减，而ReLU函数的导数在输入为负数时候，导数值为0，输入为正数时，导数值为1

4.模型效果不同

对于简单的数据集,sigmoid函数和ReLU函数的效果差不多。
对于复杂的数据集,ReLU函数的训练速度更快,容易达到更好的效果。这是因为ReLU函数有利于建立更深的网络结构。

综上所述，sigmoid函数的表达能力稍微弱一些,容易出现梯度消失问题,模型训练速度较慢，ReLU函数的表达能力更强,训练速度更快,更容易达到优秀的效果。

三、反向传播(Backpropagation)

一、反向传播的基本思想(正向计算-误差计算-梯度计算-参数更新)

1. 前向计算网络,得到最终输出结果。

2. 计算最终输出结果与真实标签之间的误差。

3. 从输出层开始,根据链式法则计算每个层的输入与该层的损失函数的梯度。

4. 利用梯度信息更新网络中每个层的参数,使得损失函数最小。

5. 重复步骤1-4,直到满足停止条件。

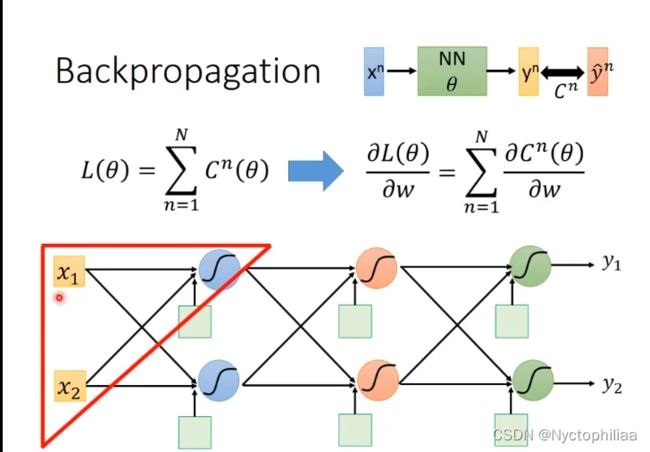
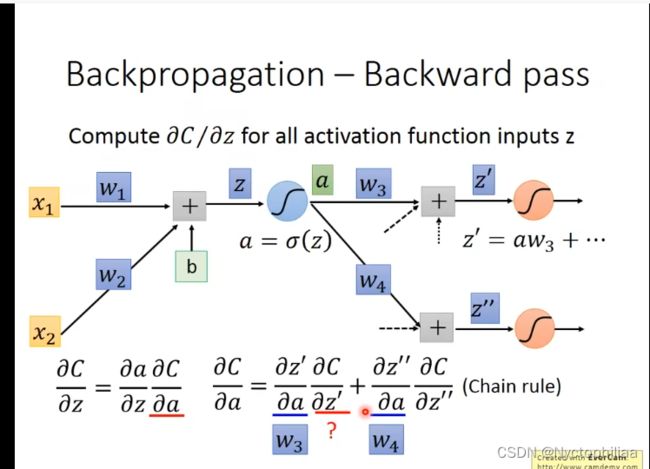
二、计算过程

其中是一系列未知参数，x是输入数据，y是经过很多隐藏层计算后得出的值，是真实值，C就是y与之间的差值。就是把所有的差值进行相加求和。

计算过程如下:

所以反向传播算法解决的就是深度网络中大规模参数优化的问题,它使得深度网络的端到端的自动训练成为可能,从而实现神经网络模型的学习和提高。这是深度学习取得巨大成功的基石之一。

总结

总的来说，机器学习的过程就是首先定义一个函数表达式，然后定义损失，调整参数使得损失值达到最小，从而使得预测值更解决真实值。下周，我将去学习关于分类与回归的问题。