【动态规划】数位统计DP

数位统计DP

1. 数位统计DP

定义

• 和数字相关，一般让我们求方案数。

• 题目一般的套路：

  （1）一般会让求解某个区间中满足某种性质的数的个数，可以转化为求[0, t]中满足条件的数的个数，如果求解[x, y]之间满足性质的数的个数，则结果为f(y) - f(x-1)，类似于前缀和的思想。

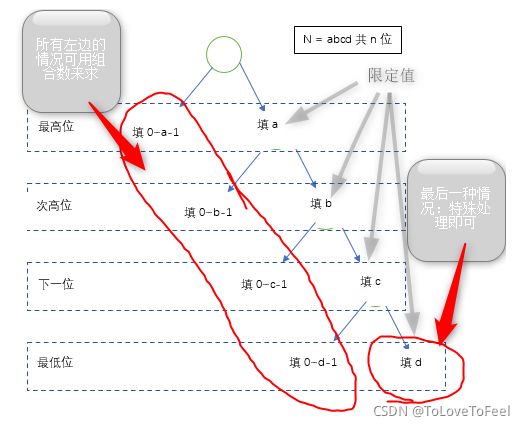
  （2）将t每一位数据抠出来，然后一位一位数字进行考虑，按照树的结构进行考虑，如下图（图片来源：网址）：

2. AcWing上的数位统计DP题目

AcWing 338. 计数问题

问题描述

• 问题链接：AcWing 338. 计数问题

  

分析

• 这一题首先需要转化一下，让我们求区间[a, b]之间各个数字出现的次数，利用前缀和的思想，假设count(n, i), 0<=i<=9可以求出1~n中i出现的次数，则最终i在[a, b]中出现的次数为count(b, i) - count(a - 1, i)。

• 下面的问题就转化为如何求1~n中某个数出现的次数，以出现1的次数为例，假设我们的数据是abcdefg，如果我们现在枚举千位是1有多少种方案，需要分类讨论（假设我们考虑的数据为xxx1yyy，则必须满足1<= xxx1yyy <=abcdeg）：

  （1）xxx=000~abc-1，则此时yyy可以取000~999，因此对应$abc\times 1000$种方案；

  （2）xxx=abc，此时还需要分为三种情况讨论：

  （2.1）d<1，此时xxx1yyy一定大于abcdefg，不存在合法情况；

  （2.2）d==1，此时yyy可以取000~efg，存在efg+1种合法情况；

  （2.3）d>1，此时yyy可以取000~999，一共有1000中合法情况。

• 对于求1~n中1、2、3、4、5、6、7、8、9都可以采用上述讨论，但是对于0出现的次数我们需要重新考虑，这是因为不能有前导0。

• 因为不能存在前导0，对于abcdefg，如果最高位a的位置放置0，则不合法，我们应该从次高位开始考虑，对于每一位，分类讨论：

  （1）xxx=001~abc-1，则此时yyy可以取000~999，因此对应$abc\times 1000-1000$种方案；

  （2）xxx=abc，此时还需要分为三种情况讨论：

  （2.1）d<0，不存在这种情况情况；

  （2.2）d==0，此时yyy可以取000~efg，存在efg+1种合法情况；

  （2.3）d>0，此时yyy可以取000~999，一共有1000中合法情况。

代码

• C++

#include 
#include 
#include 

using namespace std;

int count(int n, int x) {
    
    if (n == 0) return 0;
    
    vector<int> num;
    while (n) num.push_back(n % 10), n /= 10;
    reverse(num.begin(), num.end());
    
    int res = 0;
    for (int i = 0 + !x; i < num.size(); i++) {
        int left = 0, right = 0, p = 1;
        for (int j = 0; j < i; j++) left = left * 10 + num[j];
        for (int j = i + 1; j < num.size(); j++) {
            right = right * 10 + num[j];
            p *= 10;
        }
        
        int d = num[i];  // 当前第i位的真实数据
        if (x) {
            if (d < x) res += left * p;
            else if (d == x) res += left * p + right + 1;
            else res += (left + 1) * p;
        } else {  // 此时x为0
            if (d == x) res += (left - 1) * p + right + 1;
            else res += left * p;
        }
    }
    return res;
}

int main() {
    
    int a, b;
    while (cin >> a >> b, a || b) {
        if (a > b) swap(a, b);
        
        for (int i = 0; i <= 9; i++)
            cout << count(b, i) - count(a - 1, i) << ' ';
        cout << endl;
    }
    
    return 0;
}

#include 
#include 

using namespace std;

// 得到num[l, r]对应的数字
int get(vector<int> num, int r, int l) {
    int res = 0;
    for (int i = r; i >= l; i--)
        res = res * 10 + num[i];
    return res;
}

// 返回10^x
int power10(int x) {
    int res = 1;
    while (x --) res *= 10;
    return res;
}

// 统计出1~n中x的出现次数
int count(int n, int x) {
    
    if (n == 0) return 0;
    
    vector<int> num;
    while (n) {
        num.push_back(n % 10);
        n /= 10;
    }
    n = num.size();
    
    int res = 0;
    for (int i = n - 1 - !x; i >= 0; i--) {  // x==0时从次高位考虑
        if (i < n - 1) {
            res += get(num, n - 1, i + 1) * power10(i);
            if (!x) res -= power10(i);
        }
        
        if (num[i] == x) res += get(num, i - 1, 0) + 1;
        else if (num[i] > x) res += power10(i);
    }
    return res;
}

int main() {
    
    int a, b;
    while (cin >> a >> b, a || b) {
        if (a > b) swap(a, b);
        
        for (int i = 0; i <= 9; i++)
            cout << count(b, i) - count(a - 1, i) << " ";
        cout << endl;
    }
    return 0;
}

AcWing 1081. 度的数量

问题描述

• 问题链接：AcWing 1081. 度的数量

  

分析

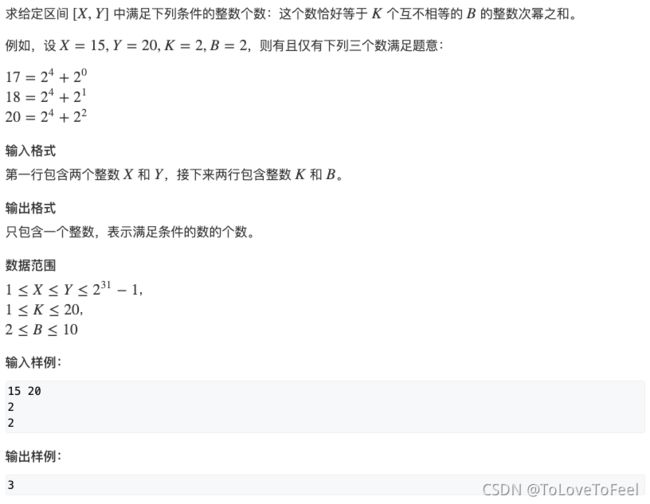
• 本题给定一个区间[X, Y]，我们要求出满足在B进制表示下，一共有K个1，其余位都是0的数的数量。

• 首先转化为求[0, n]中满足上述性质的数的个数，然后开始考虑n。

• 使用f[i][j]表示一共i位数字，其中1的数量为j个的数量，可以预处理出来。

• 从n的最高位开始考虑，并使用last表示已经使用了几个1。假设最高位数值为x，如果x为0的话，直接考虑下一位；否则这一位可以选择填0或者1，假设不包含当前位还有i位需要填写，如果当前位填写0，则一共有f[i][K-last]做法；如果x>1，则当前位填写1，则一共有f[i][K-last-1]做法，结束循环，因为当前为固定为x，然后考虑下一位一定是不合法的方案；如果x==1，直接考虑下一位即可。

• 关于数组f的求解可以使用递推求解（组合数的求解）。

代码

• C++

#include 
#include 

using namespace std;

const int N = 35;

int K, B;
int f[N][N];  // 组合数

void init() {
    
    for (int i = 0; i < N; i++)
        for (int j = 0; j <= i; j++)
            if (!j) f[i][j] = 1;
            else f[i][j] = f[i - 1][j - 1] + f[i - 1][j];
}

int dp(int n) {
    
    if (!n) return 0;
    
    vector<int> nums;
    while (n) nums.push_back(n % B), n /= B;
    
    int res = 0;
    int last = 0;  // 当前考虑的位之前1出现的次数
    for (int i = nums.size() - 1; i >= 0; i--) {
        int x = nums[i];
        
        if (x) {  // nums[i-1, ..., 0]后面还有i位
            res += f[i][K - last];  // 当前位填写0对应的方案数
            
            if (x > 1) {
                if (K >= last + 1) res += f[i][K - last - 1];  // 当前位填写1对应的方案数
                break;  // 后面的分支不用考虑了，因为当前为填写x后面无论怎么填都非法
            } else {  // x为1，当前为填写1
                last++;
                if (last > K) break;
            }
        }
        
        if (!i && K == last) res++;  // 说明n本身也是一个符合要求的数字
    }
    
    return res;
}

int main() {
    
    init();
    
    int l, r;
    cin >> l >> r >> K >> B;
    
    cout << dp(r) - dp(l - 1) << endl;
    
    return 0;
}

AcWing 1082. 数字游戏

问题描述

• 问题链接：AcWing 1082. 数字游戏

  

分析

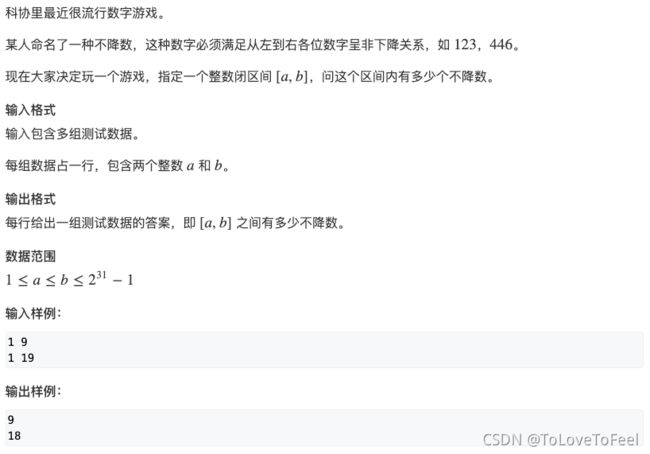
• 本题给定一个区间[a, b]，我们要求出非降数的数目。

• 可以首先求出[0, n]中非降数的个数，然后用前缀和的方式就可以求解出[a, b]中非降数的个数。

• 因为我们要考虑当前位和前一位的数字的大小关系，因此使用last记录上一位数字填写的是几。

• 使用f[i][j]表示一共有i位，且最高位填j的数的个数。

• 从最高位开始考虑，假设当前考虑的数字为x，则当前位可以填写[last, x)中的任何一个数，假设当前为填写的是j，若此时包含该位还剩余i+1未填写，则结果需要加上f[i+1][j]。

• 这里因为a、b都是大于等于1的数，按照前缀和的方式求解的话，0既可以算成非降数也可以不算成。但是在递推的过程中需要使用到0这个数据，因此必须算成非降数。

代码

• C++

#include 
#include 

using namespace std;

const int N = 11;

int f[N][N];  // f[i, j]表示一共有i位，且最高位填j的数的个数

void init() {
    
    for (int i = 0; i <= 9; i++) f[1][i] = 1;
    
    for (int i = 2; i < N; i++)
        for (int j = 0; j <= 9; j++)
            for (int k = j; k <= 9; k++)
                f[i][j] += f[i - 1][k];  // 位置关系jk，因此k>=j
}

int dp(int n) {
    
    if (!n) return 1;
    
    vector<int> nums;
    while (n) nums.push_back(n % 10), n /= 10;
    
    int res = 0;
    int last = 0;  // last 的初始值只要小于0都可以
    for (int i = nums.size() - 1; i >= 0; i--) {
        int x = nums[i];
        
        for (int j = last; j < x; j++)  // 当前填写的数据要大于等于last且小于x
            res += f[i + 1][j];
        
        if (x < last) break;  // 高位last大于当前位x，不合法，退出循环
        last = x;
        
        if (!i) res++;
    }
    
    return res;
}

int main() {
    
    init();
    
    int a, b;
    while (cin >> a >> b) {
        cout << dp(b) - dp(a - 1) << endl;
    }
    
    return 0;
}

AcWing 1083. Windy数

问题描述

• 问题链接：AcWing 1083. Windy数

  

分析

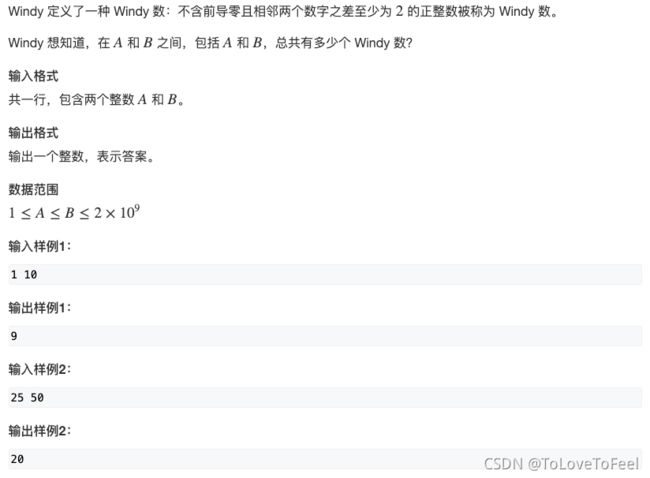
• 本题给定一个区间[a, b]，我们要求出Windy数的数目。

• 可以首先求出[0, n]中Windy数的个数，然后用前缀和的方式就可以求解出[a, b]中Windy数的个数。

• 因为我们要考虑当前位和前一位的数字的大小关系，因此使用last记录上一位数字填写的是几。

• 使用f[i][j]表示一共有i位，且最高位填j的Windy数的个数。预处理得到这个数组，这个数组允许最高位是0。

• 从最高位开始考虑每一位，当前考虑的数字为x，如果当前考虑的是最高位，则不能填0，可以填写[1, x)中的和last差的绝对值大于等于2的其他数字；如果当前考虑的不是最高位，则可以填写[0, x)中所有满足条件的数据。

• 假设当前为填写的是j，若此时包含该位还剩余i+1未填写，则结果需要加上f[i+1][j]。

• 最后还需要特殊处理有前导零的数，如果n一共有cnt位数字，则需要考虑长度为[1, cnt-1]长度的数字，最高位可以是[1, 9]。

代码

• C++

#include 
#include 

using namespace std;

const int N = 11;

int f[N][N];

// 计算的是含有前导0的windy数的个数
void init() {
    
    for (int i = 0; i <= 9; i++) f[1][i] = 1;
    
    for (int i = 2; i < N; i++)
        for (int j = 0; j <= 9; j++)
            for (int k = 0; k <= 9; k++)
                if (abs(j - k) >= 2)
                    f[i][j] += f[i - 1][k];
}

int dp(int n) {
    
    if (!n) return 0;  // 后面的计算中0没被算入是windy数，因此这里也不能算作
    
    vector<int> nums;
    while (n) nums.push_back(n % 10), n /= 10;
    
    int res = 0;
    int last = -2;  // 只要和[0~9]中的数差绝对值大于等于2即可
    for (int i = nums.size() - 1; i >= 0; i--) {
        int x = nums[i];
        
        // 如果是最高位从1开始循环，避免出现前导0
        for (int j = (i == nums.size() - 1); j < x; j++)
            if (abs(j - last) >= 2)
                res += f[i + 1][j];
        
        if (abs(x - last) >= 2) last = x;
        else break;
        
        if (!i) res++;
    }
    
    // 特殊处理有前导零的数
    for (int i = 1; i < nums.size(); i++)
        for (int j = 1; j <= 9; j++)
            res += f[i][j];
    
    return res;
}

int main() {
    
    init();
    
    int l, r;
    cin >> l >> r;
    
    cout << dp(r) - dp(l - 1) << endl;
    
    return 0;
}

AcWing 1084. 数字游戏 II

问题描述

• 问题链接：AcWing 1084. 数字游戏 II

  

分析

• 题给定一个区间[a, b]，我们要求出满足所有数字之和模N余0的数的数目。

• 可以首先求出[0, n]中满足上述性质的数的个数，然后用前缀和的方式就可以求解出[a, b]中满足上述性质的数的个数。

• 因为我们要求解出所有数字之和，因此使用last记录前面已经遍历的数字之和。

• 使用f[i][j][k]表示：一共i位数据、最高位数据是j且各位数字之和模N余数为k的数的个数。可以预处理出来这个数组。

• 因为最高位j是固定的，可以枚举次高位填的数字x，相当于一共i-1位数据、最高位数据是x且各位数字之和模N余数为k-j的数的个数，即f[i-1][x][k-j]，此状态可以转移到f[i][j][k]。

• 注意C++中余数可能为负数，因此需要实现一个取余的函数将负余数转化为正余数。

• 从最高位一次考察n的每一位数据，假设当前考察的数据为x，则当前为可以填写[0, x)中的任意一个数，且此时包含当前位以及后面没有确定的位之和的余数应该为-last。因此若此时包含该位还剩余i+1未填写，需要答案要加上f[i + 1][j][mod(-last)]。

代码

• C++

#include 
#include 
#include 

using namespace std;

const int N = 11, M = 110;

int P;
int f[N][10][M];

// 负余数转化为正余数
int mod(int x) {
    return (x % P + P) % P;
}

void init() {
    
    memset(f, 0, sizeof f);
    
    for (int i = 0; i <= 9; i++) f[1][i][i % P] = 1;
    
    for (int i = 2; i < N; i++)
        for (int j = 0; j <= 9; j++)
            for (int k = 0; k < P; k++)
                for (int x = 0; x <= 9; x++)
                    f[i][j][k] += f[i - 1][x][mod(k - j)];
}

int dp(int n) {
    
    if (!n) return 1;
    
    vector<int> nums;
    while (n) nums.push_back(n % 10), n /= 10;
    
    int res = 0;
    int last = 0;  // 已经遍历的数字之和
    for (int i = nums.size() - 1; i >= 0; i--) {
        int x = nums[i];
        
        for (int j = 0; j < x; j++)
            res += f[i + 1][j][mod(-last)];
        
        last += x;
        
        if (!i && last % P == 0) res++;
    }
    
    return res;
}

int main() {
    
    int l, r;
    while (cin >> l >> r >> P) {
        
        init();
        
        cout << dp(r) - dp(l - 1) << endl;
    }
    
    return 0;
}

AcWing 1085. 不要62

问题描述

• 问题链接：AcWing 1085. 不要62

  

分析

• 本题给定一个区间[a, b]，我们要不含有4和62的数的数目。

• 可以首先求出[0, n]中满足上述性质的数的个数，然后用前缀和的方式就可以求解出[a, b]中满足上述性质的数的个数。

• 因为我们要考虑当前位和前一位的数字是否能组成62，因此使用last记录上一位数字填写的是几。

• 使用f[i][j]表示当前一共i+1位数字且最高位数字为j的满足上述性质的数的数量。可以通过递推得到这个数组。

• 因为最高位j是固定的，可以枚举次高位填的数字k，如果k==4或者jk可以组成62则不是合法方案，则不应该统计。f[i][j]可以由f[i-1][k]转移过来。

• 从最高位开始考虑每一位，当前考虑的数字为x，如果x==4或者x==2 && last==6则直接结束循环。否则我们可以枚举当前为填写[0, x)中的数j（当然要满足上述两个条件），若此时包含该位还剩余i+1未填写，需要答案要加上f[i+1][j]。

代码

• C++

#include 
#include 

using namespace std;

const int N = 11;

int f[N][10];

void init() {
    
    for (int i = 0; i <= 9; i++)
        if (i != 4)
            f[1][i] = 1;
    
    for (int i = 2; i < N; i++)
        for (int j = 0; j <= 9; j++) {
            if (j == 4) continue;
            for (int k = 0; k <= 9; k++) {
                if (k == 4 || j == 6 && k == 2) continue;
                f[i][j] += f[i - 1][k];
            }
        }
}

int dp(int n) {
    
    if (!n) return 1;
    
    vector<int> nums;
    while (n) nums.push_back(n % 10), n /= 10;
    
    int res = 0;
    int last = 0;  // 不等于6即可
    for (int i = nums.size() - 1; i >= 0; i--) {
        int x = nums[i];
        
        for (int j = 0; j < x; j++) {  // 枚举当前为填写的数字
            if (j == 4 || last == 6 && j == 2) continue;
            res += f[i + 1][j];
        }
        
        if (x == 4 || last == 6 && x == 2) break;
        last = x;
        
        if (!i) res++;
    }
    
    return res;
}

int main() {
    
    init();
    
    int l, r;
    while (cin >> l >> r, l || r) {
        cout << dp(r) - dp(l - 1) << endl;
    }
    
    return 0;
}

AcWing 1086. 恨7不成妻

问题描述

• 问题链接：AcWing 1086. 恨7不成妻

  

分析

• 本题给定一个区间[a, b]，让我们求出和7无关的数字的平方和。

• 可以首先求出[0, n]中满足上述性质的数的平方和，然后用前缀和的方式就可以求解出[a, b]中满足上述性质的数的平方和。

• 使用f[i, j, a, b]表示一共有i位数字、最高位数字是j、该数模7余数为a，该数所有位之和模7余数为b的所有数的平方和。

• 考虑哪个状态可以转移到f[i, j, a, b]，因为最高位已经固定为j，当去掉最高位后，还剩余i位，此时数变为了a-j*10^(i-1)，各位数字之和变为了b-j，对应状态是：f[i-1, k, a-j*10^(i-1), b-j]，k是此时去掉j后的最高位。

• 但是仅仅根据f[i-1, k, a-j*10^(i-1), b-j]是无法推出f[i, j, a, b]。因为：我们要推的是0~j____中满足上述性质的数的平方和，假设$j{A}_1、j{A}_2、...、j{A}_t$可以得到当前考察的数，则：

$$\begin{gathered} f[i,j,a,b]=(j{A}_1{)}^2+...+(j{A}_t{)}^2 \\ =(j\times 10^{i-1}+A_1{)}^2+...+(j\times 10^{i-1}+A_t{)}^2 \\ =(j\times 10^{i-1}{)}^2\times t+2\times j\times 10^{i-1}\times (A_1+...+A_t)+(A_1^2+...+A_t^2) \end{gathered}$$

• 根据上述表达式，我们除了记录所有满足条件数的平方和（对应上述式子中的$A_1^2+...+A_t^2$），还需要记录 $A_1+...+A_t$ 以及满足条件的数的个数t。

• 上述表达式中需要求出所有满足条件的数的和，有如下递推公式：

$$j{A}_1+...+j{A}_t=j\times 10^{i-1}\times t+(A_1+...+A_t)$$

代码

• C++

#include 
#include 
#include 

using namespace std;

typedef long long LL;

const int N = 20, P = 1e9 + 7;

// f[i][j][a][b]代表需要满足的条件如下: 
// 一共有i位数字、最高位数字是j、该数模7余数为a，该数所有位之和模7余数b
struct F {
    int s0;  // 满足条件的个数
    int s1;  // 满足条件的数之和(取模之后的结果，后面同理)
    int s2;  // 满足条件的数的平方和
} f[N][10][7][7];

int power7[N];  // power7[i] = 10^i % 7
int power9[N];  // power9[i] = 10^i % P

int mod(LL x, int y) {
    return (x % y + y) % y;
}

void init() {
    
    for (int i = 0; i <= 9; i++) {
        if (i == 7) continue;
        auto &v = f[1][i][i % 7][i % 7];
        v.s0++, v.s1 += i, v.s2 += i * i;
    }
    
    LL power = 10;  // 表示10^(i-1)
    for (int i = 2; i < N; i++, power *= 10) {  // 枚举位数
        for (int j = 0; j <= 9; j++) {  // 枚举最高位填写的数字
            if (j == 7) continue;
            for (int a = 0; a < 7; a++)  // 枚举该数模7的结果
                for (int b = 0; b < 7; b++)  // 枚举该数所有位之和模7的结果
                    for (int k = 0; k <= 9; k++) {  // 枚举次高位
                        if (k == 7) continue;
                        
                        // 根据 v2 推出 v1
                        auto &v1 = f[i][j][a][b], &v2 = f[i - 1][k][mod(a - j * power, 7)][mod(b - j, 7)];
                        v1.s0 = mod(v1.s0 + v2.s0, P);
                        v1.s1 = mod(v1.s1 + j * (power % P) % P * v2.s0 % P + v2.s1, P);
                        v1.s2 = mod(v1.s2 + 
                                    j * j * (power % P) % P * (power % P) % P * v2.s0 + 
                                    2 * j * power % P * v2.s1 + 
                                    v2.s2, 
                                P);
                    }
        }
    }
    
    power7[0] = power9[0] = 1;
    for (int i = 1; i < N; i++) {
        power7[i] = power7[i - 1] * 10 % 7;
        power9[i] = power9[i - 1] * 10ll % P;
    }
}

// 在所有位数为i，最高位为j的所有状态中抠掉数字模7余a，各位数字之和模7余b的其他状态之和
F get(int i, int j, int a, int b) {
    int s0 = 0, s1 = 0, s2 = 0;
    for (int x = 0; x < 7; x++)
        for (int y = 0; y < 7; y++)
            if (x != a && y != b) {
                auto v = f[i][j][x][y];
                s0 = (s0 + v.s0) % P;
                s1 = (s1 + v.s1) % P;
                s2 = (s2 + v.s2) % P;
            }
    return {s0, s1, s2};
}

int dp(LL n) {
    
    if (!n) return 0;
    
    LL backup_n = n % P;
    vector<int> nums;
    while (n) nums.push_back(n % 10), n /= 10;
    
    int res = 0;
    LL la = 0;  // 已经考察过的位代表的数据
    LL lb = 0;  // 已经考察过的数之和
    for (int i = nums.size() - 1; i >= 0; i--) {
        int x = nums[i];
        for (int j = 0; j < x; j++) {
            if (j == 7) continue;
            int a = mod(-la * power7[i + 1], 7);
            int b = mod(-lb, 7);
            
            auto v = get(i + 1, j, a, b);
            
            res = mod(res +
                        (la % P) * (la % P) % P * power9[i + 1] % P * power9[i + 1] % P * v.s0 % P +
                        2 * (la % P) * power9[i + 1] % P * v.s1 % P +
                        v.s2,
                  P);
        }
        
        if (x == 7) break;
        la = la * 10 + x;
        lb += x;
        
        if (!i && la % 7 && lb % 7) res = (res + backup_n * backup_n) % P;
    }
    
    return res;
}

int main() {
    
    init();
    
    int T;
    cin >> T;
    while (T--) {
        LL l, r;
        cin >> l >> r;
        cout << mod(dp(r) - dp(l - 1), P) << endl;
    }
    
    return 0;
}

3. 力扣上的记忆化搜索题目

Leetcode 0233 数字 1 的个数

题目描述：Leetcode 0233 数字 1 的个数

分析

• 本题的考点：数学。

• 这一题最直观的做法，就是枚举1~n中的每个数，然后将每个数中1的个数加到res中，最后返回res。但是这种做法时间复杂度太高了。

• 另一种做法是枚举每一位上1的个数，从高位开始枚举，假设我们的数据是abcdefg，如果我们现在枚举千位是1有多少种方案，需要分类讨论：

  （1）如果d==0，则d的左边可以取0~abc-1，右边可以取0~999，此时千位取1对应的数据都小于原数，一共$abc\times 1000$种方案；

  （2）如果d==1，同样左边可以取0~abc-1，右边可以取0~999，一共$abc\times 1000$种方案；另外左边可以取abc，右边可以取0~efg，对应$efg+1$种方案，因此一共$abc\times 1000+efg+1$种方案。

  （3）如果d>1，左边可以取0~abc，右边可以取0~999，一共$(abc+1)\times 1000$种方案。

• 下面的代码中用left记录上面演示的abc，用right记录上面演示的efg。

代码

• C++

class Solution {
public:
    int countDigitOne(int n) {
        
        if (n <= 0) return 0;
        vector<int> nums;
        while (n) nums.push_back(n % 10), n /= 10;
        reverse(nums.begin(), nums.end());  // 为了让nums[0]对应最高位
        int res = 0;
        for (int i = 0; i < nums.size(); i++) {
            int d = nums[i];
            int left = 0, right = 0, p = 1;  // p存储10的次幂
            for (int j = 0; j < i; j++) left = left * 10 + nums[j];
            for (int j = i + 1; j < nums.size(); j++) {
                right = right * 10 + nums[j];
                p *= 10;
            }
            if (d == 0) res += left * p;
            else if (d == 1) res += left * p + right + 1;
            else res += (left + 1) * p;
        }
        return res;
    }
};

• Java

class Solution {
    public int countDigitOne(int n) {

        if (n <= 0) return 0;
        int[] nums = new int[10];
        int len = 0;
        while (n != 0) {
            nums[len++] = n % 10; n /= 10;
        }
        // 此时nums[0]对应最低位
        int res = 0;
        for (int i = 0; i < len; i++) {
            int d = nums[i];
            int left = 0, right = 0, p = 1;  // p存储10的次幂
            for (int j = len - 1; j > i; j--) left = left * 10 + nums[j];
            for (int j = i - 1; j >= 0; j--) {
                right = right * 10 + nums[j];
                p *= 10;
            }
            if (d == 0) res += left * p;
            else if (d == 1) res += left * p + right + 1;
            else res += (left + 1) * p;
        }
        return res;
    }
}

时空复杂度分析

• 时间复杂度：$O(lo{g}^2(n))$。其实可以优化成$O(log(n))$的，只需要预处理出left、right即可。

• 空间复杂度：$O(1)$。