二叉树的OJ练习（一）

目录

序列文章

单值二叉树

相同的树

对称二叉树 

二叉树的前序遍历

---

序列文章

初识树（C语言）：http://t.csdnimg.cn/eqFmT

二叉树的基本概念（C语言）：http://t.csdnimg.cn/AkwTC

大小堆的实现（C语言）：http://t.csdnimg.cn/yoXVC

看了就会的堆排序（C语言）：http://t.csdnimg.cn/EWzgM

top K问题（借你五分钟）：http://t.csdnimg.cn/1YLT8

堆的相关时间复杂度计算（C语言）：http://t.csdnimg.cn/OSAr4

二叉树的前、中、后序遍历的实现：http://t.csdnimg.cn/xNHrs

计算二叉树结点个数、叶子结点个数的代码实现：http://t.csdnimg.cn/kiBpd

二叉树查找值为x的结点、树的高度、第k层结点个数的代码实现：http://t.csdnimg.cn/BcFEW

二叉树的创建、销毁、层序遍历、层序遍历进阶的代码实现：http://t.csdnimg.cn/Qlxu0

二叉树的OJ练习（一）：http://t.csdnimg.cn/jhOWW

二叉树的OJ练习（二） ：http://t.csdnimg.cn/sl7kl

<你想看的我这里都有 >

单值二叉树

965. 单值二叉树 - 力扣（LeetCode）

题目：如果二叉树每个节点都具有相同的值，那么该二叉树就是单值二叉树。只有给定的树是单值二叉树时，才返回 true；否则返回 false。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */
bool isUnivalTree(struct TreeNode* root) {
    if(root==NULL)
        return true;

    if(root->left&&root->val!=root->left->val)
        return false;
    
    if(root->right&&root->val!=root->right->val)
        return false;
    
    return isUnivalTree(root->left) && isUnivalTree(root->right);

}

解释： 

1、首先当树为空树时，并不违反规定，可以直接返回true

2、当不为空树时，先判断其左右子树是否存在，如果左子树不存在，则继续判断右子树是否存在，若两者都不存在则进行下一次的递归判断

3、当左子树存在时，用当前结点的值与其左子树的根结点的值作比较，如果不相等就返回false

4、当右子树存在时，用当前结点的值与其右子树的根结点的值作比较，如果不相等就返回false

相同的树

100. 相同的树 - 力扣（LeetCode）

题目：给你两棵二叉树的根节点 p 和 q ，编写一个函数来检验这两棵树是否相同。如果两个树在结构上相同，并且节点具有相同的值，则认为它们是相同的。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */
bool isSameTree(struct TreeNode* p, struct TreeNode* q) {
    //如果均为空
    if(p == NULL && q == NULL)
        return true;

    //如果其中一个为空
     if(p == NULL || q == NULL)
        return false;
        
    //如果都不为空，且不等
    if(p->val != q-> val)
        return false;

   //递归比较左子树与右子树
   return isSameTree(p->left,q->left) && isSameTree(p->right,q->right);
}

解释： 

1、先比较两个树的根节点，如果均为空，则两树虽为空树，但仍相等，返回true

2、若两个树中的根节点有一个为空，那么两个树一定不相等，返回flase

3、如果两个树的根节点均不为空，比较它们的值，如果不相等返回flase 

4、比较完两棵树的根节点后，再比较两颗树的左子树和右子树，即isSameTree(p->left,q->left)与

isSameTree(p->right,q->right)

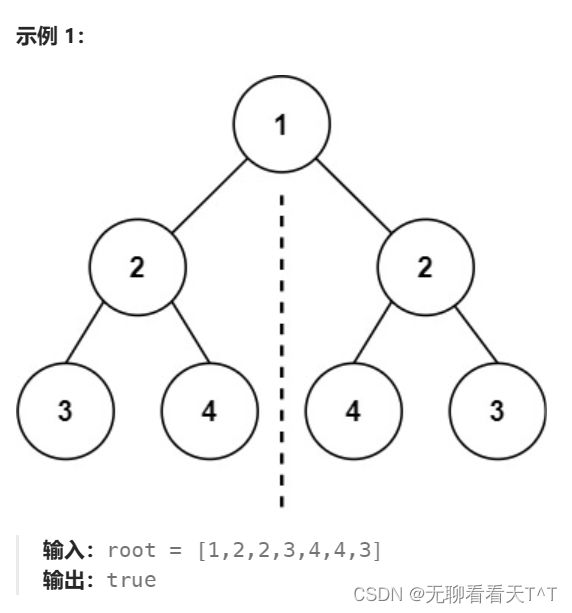
对称二叉树 

101. 对称二叉树 - 力扣（LeetCode）

题目：给你一个二叉树的根节点 root ， 检查它是否轴对称

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */

bool judge(struct TreeNode* p,struct TreeNode* q)
{
      //如果左右子树均为空，则该树对称
     if(p == NULL && q == NULL )
        return true;

      //如果左右子树有一个为空，那么该树就不对称
    if(p== NULL || q== NULL)
        return false;

    //如果左右子树根节点的值不相等，那么该树不对称
    if(p->val != q->val)
        return false;
    //递归其左右子树
    return judge(p->left,q->right) && judge(p->right,q->left);
}

bool isSymmetric(struct TreeNode* root) {
    //如果为空树，那么该树就对称
    if(root == NULL)
        return true;

    return judge(root->left,root->right);
}

解释： 

1、当一棵树为空树时，该树对称，返回true

2、判断根节点的左右子树的根节点，如果两个结点均为空，则树只有一个根节点，该树对称，然会true

3、如果两个结点只有一个为空，则树不对称，返回false

4、如果两个结点均不为空，且两个结点的值均不相同，树不对称，返回false

5、递归左子树的左子树与右子树的右子树，如果均相同则返回true（重要）

6、递归左子树的右子树与右子树的左子树，如果均相同则返回true（重要）

7、如果两次递归均返回true，则judge函数返回true

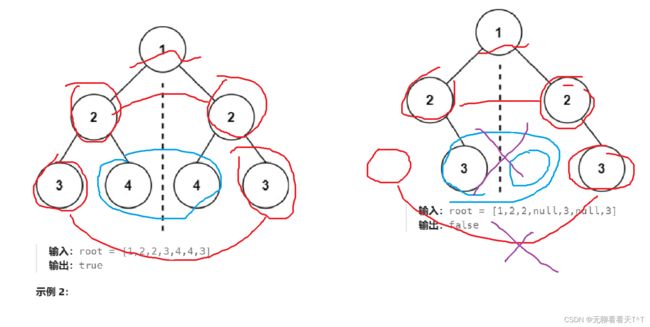
总结：对于C语言而言采用这种解法完成本题必须使用两个函数，因为这里的判断二叉树是否对称，不仅仅是要整体上对称，而且值也要对称，如果只能传递一个参数那么就只能先比较完一个完整的左子树然后再去比较另一个完整的右子树，很明显这样无法完成我们的目标的，所以我们要引入一个新的judge函数来获取树的根节点的左右子树的根节点，然后经过一系列基本的判断后，进行那两步十分重要的递归：

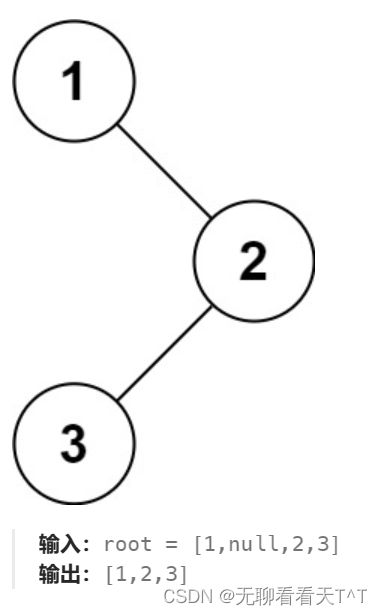
二叉树的前序遍历

144. 二叉树的前序遍历 - 力扣（LeetCode）

题目：给你二叉树的根节点 root ，返回它节点值的 前序 遍历

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */
/**
 * Note: The returned array must be malloced, assume caller calls free().
 */

///获取二叉树中结点个数
int TreeSize(struct TreeNode* root)
{
    return root == NULL ? 0 : TreeSize(root->left) + TreeSize(root->right) + 1; 
}

//前序遍历
void  PrevOrder(struct TreeNode* root,int* a,int* pi)
{
    if(root == NULL)
        return;
    
    a[(*pi)++] = root->val;
    PrevOrder(root->left,a,pi);
    PrevOrder(root->right,a,pi);

}

//输出型参数returnSize
int* preorderTraversal(struct TreeNode* root, int* returnSize) {
    
    int n = TreeSize(root);
    int* a = (int*)malloc(sizeof(int) * n);
    *returnSize = n;

    int i = 0;
    PrevOrder(root,a,&i);
    return a;
}

 解释：

1、leetcode题目中常常会出现returnSize，我们叫它输出型参数，在这里它表示要返回二叉树结点的个数，所以我们还需要利用之前学过的TreeSize函数额外的计算二叉树结点的个数，最后将计算的返回值n赋值给*returnSize（returnSize是指针，用*以修改它的值）

2、除了returnSize外，题目要求我们以数组的形式返回二叉树前序遍历的结点，所以我们还要开辟一个数组a，为了确保代码不是硬代码，所以我们使用malloc来开辟数组的空间，开辟的空间大小由我们计算的二叉树结点的个数n决定

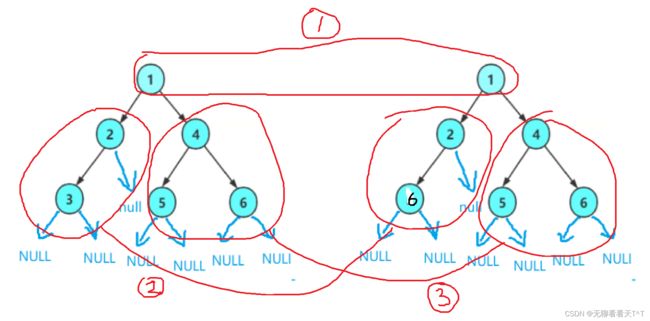
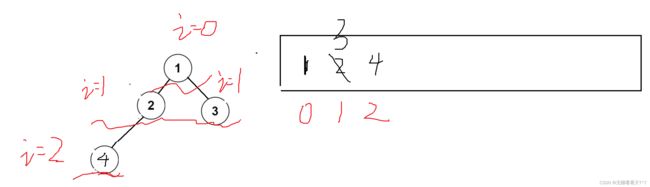
3、进行前序遍历时，我们要传入的参数除了二叉树的根节点以外，还需要传入数组a的指针，以及用于表示数组下标的i的地址（i初始化值为0，如果传入的不是地址，当左子树遍历完后开始遍历右子树时，i的值也会回到原来的值而不是递增下去，因为每一次的递归开辟帧栈的过程中，i因为不是全局变量所以每一块的帧栈中都会有一个i，下图中结点1开始递归左右子树时，左子树走到底时i=2，但是右子树中的i存放的依然是刚开始递归时i的值，所以如果开始递归右子树那么3会将原来的2代替，存放二叉树前序遍历结果的数组也就由原来预期的1243变为了134）

4、PrevOrder函数前序遍历时，要注意使用a[(*pi)++] = root->val向数组中存值时，一定要使用（*pi）而非pi（原因就是3中提到的）

~over~