二叉树的OJ练习（二）

目录

序列文章

通过前序遍历数组构建二叉树

二叉树的中序遍历

二叉树的后续遍历

另一棵树的子树

---

序列文章

初识树（C语言）：http://t.csdnimg.cn/eqFmT

二叉树的基本概念（C语言）：http://t.csdnimg.cn/AkwTC

大小堆的实现（C语言）：http://t.csdnimg.cn/yoXVC

看了就会的堆排序（C语言）：http://t.csdnimg.cn/EWzgM

top K问题（借你五分钟）：http://t.csdnimg.cn/1YLT8

堆的相关时间复杂度计算（C语言）：http://t.csdnimg.cn/OSAr4

二叉树的前、中、后序遍历的实现：http://t.csdnimg.cn/xNHrs

计算二叉树结点个数、叶子结点个数的代码实现：http://t.csdnimg.cn/kiBpd

二叉树查找值为x的结点、树的高度、第k层结点个数的代码实现：http://t.csdnimg.cn/BcFEW

二叉树的创建、销毁、层序遍历、层序遍历进阶的代码实现： http://t.csdnimg.cn/Qlxu0

二叉树的OJ练习（一）：http://t.csdnimg.cn/jhOWW

二叉树的OJ练习（二） ：http://t.csdnimg.cn/sl7kl

<你想看的我这里都有 >

通过前序遍历数组构建二叉树

题目：通过前序遍历的数组（ABD##E#H##CF##G##）构建二叉树

TreeNode* TreeCreat(char* a,int* pi)
{
    if(a[*pi] == '#')
    {
        (*pi)++;
        return NULL;    
    }
    
    TreeNode* root = (TreeNode*)malloc(sizeof(TreeNode));
    if(root == NULL)
    {
        perror("malloc fail");
        exit(-1);
    }
    root->data = a[(*pi)++];
    
    root->left = TreeCreat(a,pi);
    root->right = TreeCreat(a,pi);
    return root; 
}

解释：

1、 pi表示数组下标，初始值为0，a表示前序遍历的数组

2、如果检测到数组中表示空的符号'#'，那么就下标继续向前走，然后返回空，证明这一条路已经走到头了

3、如果检测到的不是'#'，那么就为该结点开辟一个内存空间，同时做开辟失败的警告条件判断

4、开辟成功后向该内存空间中存放值，值的大小为a[(*pi)++]（先使用*pi然后pi才会++，即下标向前走）

5、由于是根->左->右的前序遍历，所以应该先递归左子树，当整棵树的左子树走到底的时候就会读取到'#'，然后就会返回NULL（由于我们已经知道了非空与空的位置，整个构建的过程就相当于一个填空的过程，所以我们再进行递归的时候，TreeCreat函数传递的是前序遍历数组a和数组下标pi的地址，而不是root->left和root->right，）

6、最后记得返回二叉树的根节点

二叉树的中序遍历

题目：给定一个二叉树的根节点 root ，返回它的中序遍历 

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */
/**
 * Note: The returned array must be malloced, assume caller calls free().
 */

int TreeSize(struct TreeNode* root)
{
    return root == NULL ? 0 : TreeSize(root->left) + TreeSize(root->right) + 1; 
}

void InOrder(struct TreeNode* root,int* a,int* pi)
{
    if(root == NULL)
        return ;
    InOrder(root->left,a,pi);
    
    a[(*pi)++] = root->val;
    InOrder(root->right,a,pi);
}


int* inorderTraversal(struct TreeNode* root, int* returnSize) {
    int n = TreeSize(root);
    int* a = (int*)malloc(sizeof(int)*n);
    *returnSize = n ;

    int i = 0;
    InOrder(root,a,&i);
    
    return a;
}

解释：

1、二叉树的中序遍历与前序遍历的内容基本一致

2、唯一需要注意的就是只有当递归至左子树至空后，才开始向数组中存放数据，存放完之后再去递归它的右子树......

3、记得返回数组a

二叉树的后续遍历

题目：给定一个二叉树的根节点 root ，返回它的后序遍历 

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */
/**
 * Note: The returned array must be malloced, assume caller calls free().
 */

int TreeSize(struct TreeNode* root)
{
    return root == NULL ? 0 : TreeSize(root->left) + TreeSize(root->right) + 1; 
}

void postOrder(struct TreeNode* root,int* a,int* pi)
{
    if(root == NULL)
        return ;
    postOrder(root->left,a,pi);
    postOrder(root->right,a,pi);
    a[(*pi)++] = root->val;
  
}


int* postorderTraversal(struct TreeNode* root, int* returnSize) {
    int n = TreeSize(root);
    int* a = (int*)malloc(sizeof(int)*n);
    *returnSize = n ;

    int i = 0;
    postOrder(root,a,&i);
    
    return a;
}

解释：

1、真没啥好解释的

2、先递归完左子树，然后再递归完右子树，然后再存值

3、还是记得返回数组a

总结：对于二叉树的前、中、后序遍历，主要的区别就是存值的位置，前序遍历是先存值然后再递归它的左子树和右子树，中序遍历是先递归其左子树然后存值最后递归它的右子树，后续遍历是先存递归其左子树和右子树最后再存值（代码的实现与前中后序遍历的性质相关）

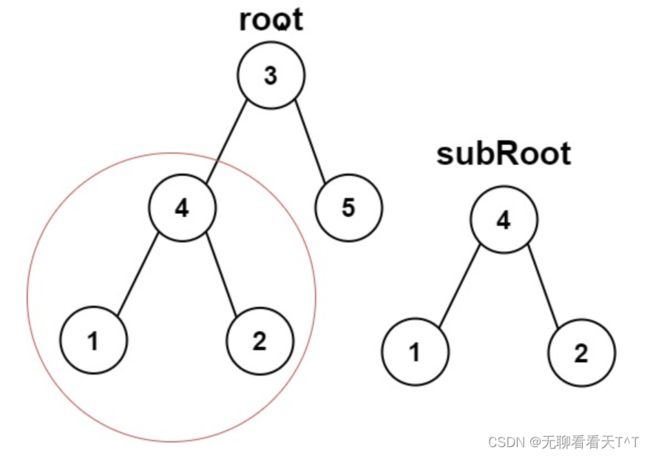
另一棵树的子树

题目：给你两棵二叉树 root 和 subRoot 。检验 root 中是否包含和 subRoot 具有相同结构和节点值的子树。如果存在，返回 true ；否则，返回 false 。二叉树 tree 的一棵子树包括 tree 的某个节点和这个节点的所有后代节点。tree 也可以看做它自身的一棵子树。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */

bool issame(struct TreeNode*p,struct TreeNode*q){
    //如果全为空，返回true
    if(p == NULL && q == NULL)
        return true;


    //如果有一个为空，返回false
    if(p == NULL || q == NULL)
        return false;

    //都不为空且值不相等，返回false
    if(p->val != q->val)
        return false;

    //如果都不为空且值相等，则递归root和subRoot的左子树和右子树
    return issame(p->left,q->left) && issame(p->right,q->right);
}

bool isSubtree(struct TreeNode* root, struct TreeNode* subRoot){
    //如果root为空，则返回false
    if(root==NULL)
        return false;

    //当root此时的值与subRoot此时的值相等时，开始递归两棵树
    if(root->val==subRoot->val) 
    {
        //如果递归后发现两棵树的左右子树均相同，返回true
        if(issame(root,subRoot))
            return true;
    }
    //如果root此时的值不等于subRoot此时的值，
    //则先递归root的左子树然后再递归它的右子树，只要有一个子树递归的返回结果为真则证明subRorrt是root的一棵子树
    return isSubtree(root->left,subRoot) || isSubtree(root->right,subRoot);
}

解释：

1、root为空的判断条件并不是限制刚开始的root的，题目中已规定了树的结点个数大于1，实际上它是为了判断左或右子树走到底是否有root->val == subRoot->val的值，如果没有就返回false

2、当找到root->val == subRoot->val的时候，开始分别递归root和subRoot的左右子树

3、注意判断只有一个为空和判断全空的顺序不能交换，因为当开始递归两棵树的左右子树时，如果在只检测到一个为空的情况下就返回false过于片面，如果此时另一颗树的位置非空，那么才能返回false，如果另一棵树此时的位置也为空，那么证明到这里之前两棵树的结点内容应该是相同的，到这里两棵树都走到了空，应该返回true然后开始另外的递归

 ~over~