【算法设计与分析】分治-时间复杂度计算
目录
- 主定理 Master Theorem
-
-
- 分治算法运行时间的递归表示
- 主定理的简化形式
- 主定理的一般形式
-
- 递归树 Recursion Tree
-
- 递归树的简单结论
主定理 Master Theorem
分治算法运行时间的递归表示
将原问题分解成 a 个子问题递归求解,每个子问题的规模是原问题的 1/b。同时子问题合并成原问题的时间为 n c n^c nc ,n 是原问题的规模。
对应的时间复杂度表达式: T ( n ) = a T ( n / b ) + O ( n c ) T(n) = aT(n/b) + O(n^c) T(n)=aT(n/b)+O(nc) ,对应的要求 a > = 1 a >=1 a>=1、 b > = 2 b>=2 b>=2、 c > = 0 c>=0 c>=0。
主定理的简化形式
T ( n ) = a T ( n / b ) + O ( n c ) T(n) = aT(n/b) + O(n^c) T(n)=aT(n/b)+O(nc) ,要求 a > = 1 a >=1 a>=1、 b > = 2 b>=2 b>=2、 c > = 0 c>=0 c>=0、 T ( 1 ) = O ( 1 ) T(1) = O(1) T(1)=O(1)。
- 如果 a < b c a < b^c a<bc,那么 T ( n ) = O ( n c ) T(n) = O(n^c) T(n)=O(nc)
- 如果 a = b c a = b^c a=bc,那么 T ( n ) = O ( n c l o g n ) T(n) = O(n^clogn) T(n)=O(nclogn)
- 如果 a > b c a > b^c a>bc,那么 T ( n ) = O ( n l o g b a ) T(n) = O(n^{log_ba}) T(n)=O(nlogba)
二分搜索:
时间复杂度: T ( n ) = T ( n / 2 ) + 1 T(n)=T(n/2)+1 T(n)=T(n/2)+1
a = 1 a=1 a=1、 b = 2 b=2 b=2、 c = 0 c=0 c=0
对应 a = b c a=b^c a=bc,因此 T ( n ) = n 0 l o g n = l o g n T(n)=n^0logn=logn T(n)=n0logn=logn
归并排序:
时间复杂度: T ( n ) = 2 T ( n / 2 ) + O ( n ) T(n)=2T(n/2)+O(n) T(n)=2T(n/2)+O(n)
a = 2 a=2 a=2、 b = 2 b=2 b=2、 c = 1 c=1 c=1
对应 a = b c a=b^c a=bc,因此 T ( n ) = n 1 l o g n = n l o g n T(n)=n^1logn=nlogn T(n)=n1logn=nlogn
多项式乘法(直接分治):
时间复杂度: T ( n ) = 4 T ( n / 2 ) + O ( n ) T(n)=4T(n/2)+O(n) T(n)=4T(n/2)+O(n)
a = 4 a=4 a=4、 b = 2 b=2 b=2、 c = 1 c=1 c=1
对应 a > b c a>b^c a>bc,因此 T ( n ) = n l o g 2 4 = n 2 T(n)=n^{log_24}=n^2 T(n)=nlog24=n2
多项式乘法(递归优化,Karatsuba算法):
时间复杂度: T ( n ) = 3 T ( n / 2 ) + O ( n ) T(n)=3T(n/2)+O(n) T(n)=3T(n/2)+O(n)
a = 3 a=3 a=3、 b = 2 b=2 b=2、 c = 1 c=1 c=1
对应 a > b c a>b^c a>bc,因此 T ( n ) = n l o g 2 3 = n 1 . 58 T(n)=n^{log_23}=n^1.58 T(n)=nlog23=n1.58
矩阵乘法(直接分治):
时间复杂度: T ( n ) = 8 T ( n / 2 ) + O ( n 2 ) T(n)=8T(n/2)+O(n^2) T(n)=8T(n/2)+O(n2)
a = 8 a=8 a=8、 b = 2 b=2 b=2、 c = 2 c=2 c=2
对应 a > b c a>b^c a>bc,因此 T ( n ) = n l o g 2 8 = n 3 T(n)=n^{log_28}=n^3 T(n)=nlog28=n3
矩阵乘法(Strassen算法):
时间复杂度: T ( n ) = 7 T ( n / 2 ) + O ( n 2 ) T(n)=7T(n/2)+O(n^2) T(n)=7T(n/2)+O(n2)
a = 7 a=7 a=7、 b = 2 b=2 b=2、 c = 2 c=2 c=2
对应 a > b c a>b^c a>bc,因此 T ( n ) = n l o g 2 7 = n 2.81 T(n)=n^{log_27}=n^{2.81} T(n)=nlog27=n2.81
主定理的一般形式
一般 主定理的简化形式 可以满足大部分的分治算法的时间复杂度分析,但是也存在 简化主定理 不适用的情况:
- 子问题数量不是常数:
- T ( n ) = n T ( n / 2 ) + O ( n 2 ) T(n) = nT(n/2) + O(n^2) T(n)=nT(n/2)+O(n2)
- 子问题数量小于1:
- T ( n ) = 1 / 2 T ( n / 2 ) + O ( n 2 ) T(n) = 1/2 T(n/2) + O(n^2) T(n)=1/2T(n/2)+O(n2)
- 分解原问题与合并子问题的总时间并不是 n c n^c nc
- T ( n ) = 2 T ( n / 2 ) + O ( n l o g n ) T(n) = 2T(n/2) + O(nlogn) T(n)=2T(n/2)+O(nlogn)
因此,使用更广泛的主定理的一般形式:
T ( n ) = a T ( n / b ) + f ( n ) T(n) = aT(n/b) + f(n) T(n)=aT(n/b)+f(n) ,要求 a > 0 a > 0 a>0、 b > 1 b>1 b>1、 T ( 1 ) = O ( 1 ) T(1) = O(1) T(1)=O(1)。
- 如果 ∃ ϵ > 0 ∃ϵ > 0 ∃ϵ>0 使 f ( n ) = O ( n l o g b a − ϵ ) f(n) = O(n^{log_ba-ϵ}) f(n)=O(nlogba−ϵ),那么 T ( n ) = Θ ( n l o g b a ) T(n) = Θ(n^{log_ba}) T(n)=Θ(nlogba)
- 如果 ∃ k > = 0 ∃k >= 0 ∃k>=0 使 f ( n ) = O ( n l o g b a l o g k n ) f(n) = O(n^{log_ba}log^kn) f(n)=O(nlogbalogkn),那么 T ( n ) = Θ n l o g b a l o g k + 1 n ) T(n) = Θn^{log_ba}log^{k+1}n) T(n)=Θnlogbalogk+1n)
- 如果 ∃ ϵ > 0 ∃ϵ > 0 ∃ϵ>0 使 f ( n ) = Ω ( n l o g b a + ϵ ) f(n) = Ω(n^{log_ba+ϵ}) f(n)=Ω(nlogba+ϵ),且对于某个常数 c < 1 c < 1 c<1和足够大的 n n n有 a f ( n / b ) < = c f ( n ) af(n/b)<=cf(n) af(n/b)<=cf(n),那么 T ( n ) = Θ ( f ( n ) ) T(n) = Θ(f(n)) T(n)=Θ(f(n))
通俗的来解释,就是看 n l o g b a n^{log_ba} nlogba 与 f ( n ) f(n) f(n) 的增长率大小:
- 情况一: n l o g b a n^{log_ba} nlogba 比 f ( n ) f(n) f(n) 的增长更快
- 情况二: n l o g b a n^{log_ba} nlogba 与 f ( n ) f(n) f(n) 的增长快慢类似
- 情况三: n l o g b a n^{log_ba} nlogba 比 f ( n ) f(n) f(n) 的增长更慢
情况一
n l o g b a n^{log_ba} nlogba 比 f ( n ) f(n) f(n) 的增长更快,至少要快 Θ ( n ϵ ) Θ(n^ϵ) Θ(nϵ)倍。
T ( n ) = 9 T ( n / 3 ) + n T(n) = 9T(n/3) + n T(n)=9T(n/3)+n
n l o g b a = n 2 n^{log_ba} = n^2 nlogba=n2 , f ( n ) = n = O ( n 2 − ϵ ) f(n) = n = O(n^{2-ϵ}) f(n)=n=O(n2−ϵ), 0 < ϵ < = 1 0< ϵ <= 1 0<ϵ<=1
因此 T ( n ) = O ( n 2 ) T(n) = O(n^2) T(n)=O(n2)
情况二
n l o g b a n^{log_ba} nlogba 与 f ( n ) f(n) f(n) 的增长快慢类似,同时 f ( n ) f(n) f(n)要比 n l o g b a n^{log_ba} nlogba快 Θ ( l o g k n ) Θ(log^kn) Θ(logkn)倍。
T ( n ) = T ( 2 n / 3 ) + 1 T(n) = T(2n/3) + 1 T(n)=T(2n/3)+1
n l o g b a = n l o g 3 / 2 1 = n 0 = 1 n^{log_ba} = n^{log_{3/2}1} = n^0 = 1 nlogba=nlog3/21=n0=1, f ( n ) = 1 = Θ ( n l o g b a l o g 0 n ) f(n) = 1 = Θ(n^{log_ba}log^0n) f(n)=1=Θ(nlogbalog0n)
因此 T ( n ) = Θ ( l o g n ) T(n) = Θ(logn) T(n)=Θ(logn)
情况三
f ( n ) f(n) f(n) 比 n l o g b a n^{log_ba} nlogba 的增长更快,至少要快 Θ ( n ϵ ) Θ(n^ϵ) Θ(nϵ)倍,且 a f ( n / b ) ≤ c f ( n ) af(n/b) ≤ cf(n) af(n/b)≤cf(n)。
T ( n ) = 3 T ( n / 4 ) + n l o g n T(n) = 3T(n/4) + n log n T(n)=3T(n/4)+nlogn
n l o g b a = n l o g 4 3 = n 0.793 n^{log_ba} = n^{log_43} = n^{0.793} nlogba=nlog43=n0.793, f ( n ) = n l o g n = Ω ( n l o g 4 3 + ϵ ) f(n) = nlogn = Ω(n^{log_43+ϵ}) f(n)=nlogn=Ω(nlog43+ϵ), ϵ ≤ 0.207 ϵ ≤ 0.207 ϵ≤0.207
并且 a f ( n / b ) = 3 f ( n / 4 ) = 3 ( n / 4 ) l o g ( n / 4 ) ≤ ( 3 / 4 ) n l o g n = c f ( n ) af(n/b) = 3f(n/4) = 3(n/4)log(n/4) ≤ (3/4)nlogn = cf(n) af(n/b)=3f(n/4)=3(n/4)log(n/4)≤(3/4)nlogn=cf(n), c = 3 / 4 c= 3/4 c=3/4
因此 T ( n ) = Θ ( n l o g n ) T(n) = Θ(nlogn) T(n)=Θ(nlogn)
使用主定理一般形式求解时间复杂度:
T ( n ) = 8 T ( n / 2 ) + Θ ( 1 ) T(n) = 8T(n/2) + Θ(1) T(n)=8T(n/2)+Θ(1)
n l o g b a n^{log_ba} nlogba = n 3 n^3 n3, f ( n ) = Θ ( 1 ) = O ( n 3 − ϵ ) f(n) = Θ(1) = O(n^{3-ϵ}) f(n)=Θ(1)=O(n3−ϵ),对于 ϵ < 3 ϵ<3 ϵ<3成立
因此 T ( n ) = Θ ( n l o g b a ) T(n)=Θ(n^{log_ba}) T(n)=Θ(nlogba) = Θ ( n 3 ) = Θ(n^3) =Θ(n3)
T ( n ) = 7 T ( n / 2 ) + Θ ( n 2 ) T(n) = 7T(n/2) + Θ(n^2) T(n)=7T(n/2)+Θ(n2)
n l o g b a n^{log_ba} nlogba = n l o g 2 7 = n^{log_27} =nlog27 = n 2.81 = n^{2.81} =n2.81, f ( n ) = Θ ( n 2 ) = O ( n 2.81 − ϵ ) f(n) = Θ(n^2) = O(n^{2.81-ϵ}) f(n)=Θ(n2)=O(n2.81−ϵ),对于 ϵ < 0.8 ϵ<0.8 ϵ<0.8成立
因此 T ( n ) = Θ ( n l o g b a ) T(n)=Θ(n^{log_ba}) T(n)=Θ(nlogba) = Θ ( n 2.81 ) = Θ(n^{2.81}) =Θ(n2.81)
T ( n ) = 2 T ( n / 2 ) + Θ ( n ) T(n) = 2T(n/2) + Θ(n) T(n)=2T(n/2)+Θ(n)
n l o g b a n^{log_ba} nlogba = n l o g 2 2 = n = n^{log_22} = n =nlog22=n, f ( n ) = Θ ( n ) f(n) = Θ(n) f(n)=Θ(n),二者增长率类似。
并且 f ( n ) = Θ ( n ) = Θ ( n l o g 2 2 l o g 0 n ) f(n) = Θ(n) = Θ(n^{log_22}log^0n) f(n)=Θ(n)=Θ(nlog22log0n)
因此 T ( n ) = Θ ( n l o g n ) T(n) = Θ(nlogn) T(n)=Θ(nlogn)
T ( n ) = 2 T ( n / 2 ) + n l o g n T(n) = 2T(n/2) + nlogn T(n)=2T(n/2)+nlogn
n l o g b a n^{log_ba} nlogba = n l o g 2 2 = n = n^{log_22} = n =nlog22=n, f ( n ) = n l o g n = Θ ( n l o g b a l o g 1 n ) f(n) = nlogn = Θ(n^{log_ba} log^1n) f(n)=nlogn=Θ(nlogbalog1n)
注意:虽然 f ( n ) f(n) f(n)要比 n l o g b a n^{log_ba} nlogba,,但没有快 n ϵ n^ϵ nϵ,因此不适用于情况三。
因此 T ( n ) = Θ ( n l o g n ) T(n) = Θ(nlogn) T(n)=Θ(nlogn)
主定理的一般形式虽然适用范围更的广,但是仍然有不适用的情况:
- n l o g b a n^{log_ba} nlogba 和 f ( n ) f(n) f(n) 的增长率不能比
- n l o g b a n^{log_ba} nlogba 比 f ( n ) f(n) f(n) 增长的更快,但没有快 Θ ( n ϵ ) Θ(n^ϵ) Θ(nϵ)倍
- f ( n ) f(n) f(n) 比 n l o g b a n^{log_ba} nlogba 增长的更快,但没有快 Θ ( n ϵ ) Θ(n^ϵ) Θ(nϵ)倍
T ( n ) = 2 T ( n / 2 ) + n / l o g n T(n) = 2T(n/2) + n/log n T(n)=2T(n/2)+n/logn
n l o g b a = n nlogb a = n nlogba=n, f ( n ) = n / l o g n f(n) = n/logn f(n)=n/logn
n l o g b a nlogb a nlogba 比 f ( n ) f(n) f(n) 增长的更快,但也只快 Θ ( l o g n ) Θ(logn) Θ(logn),因此不适用情况1
且 f ( n ) = n / l o g n = Θ ( n l o g b a l o g − 1 n ) f(n) = n/log n = Θ(n^{logb a} log^{−1} n) f(n)=n/logn=Θ(nlogbalog−1n), k = − 1 k=-1 k=−1,因此也不适用于情况2
递归树 Recursion Tree
递归树:有根树,根节点代表原问题,根节点以外的所有节点都代表一个子问题。节点的值代表解决该子问题所花费的除递归调用的时间。
原问题的运行时间等于该树所有节点的值的和。
递归树的叶子节点是递归的基本情况。
递归树的示例:
T ( n ) = a T ( n / b ) + f ( n ) T(n) = aT(n/b) + f(n) T(n)=aT(n/b)+f(n)
最终该公式的递归树如下图所示:
其中蓝色箭头表示递归树的每一层的时间花销之和。每一层的时间花销,相当于每一层递归是 f ( n ) f(n) f(n)产生的时间花销。
假设叶子节点的时间花销 f ( n / b L ) = 0 f(n/b^L) = 0 f(n/bL)=0,则 L = l o g b n L = log_bn L=logbn
整体的时间复杂度: T ( n ) = ∑ i = 0 L a i f ( n / b i ) T(n) = \sum_{i=0}^{L}a^if(n/b^i) T(n)=∑i=0Laif(n/bi)
递归树的简单结论
假设每⼀层节点值之和是上⼀层节点值之和的 r 倍(即构成几何级数)
- r < 1 r < 1 r<1,那么 T ( n ) = O ( f ( n ) ) T(n) = O(f(n)) T(n)=O(f(n))
- r = 1 r = 1 r=1,那么 T ( n ) = O ( f ( n ) l o g n ) T(n) = O(f(n)logn) T(n)=O(f(n)logn)
- r > 1 r > 1 r>1,那么 T ( n ) = O ( a L ) = O ( a l o g b n ) = O ( n l o g b a ) T(n) = O(a^L) = O(a^{log_bn}) = O(n^{log_ba}) T(n)=O(aL)=O(alogbn)=O(nlogba)
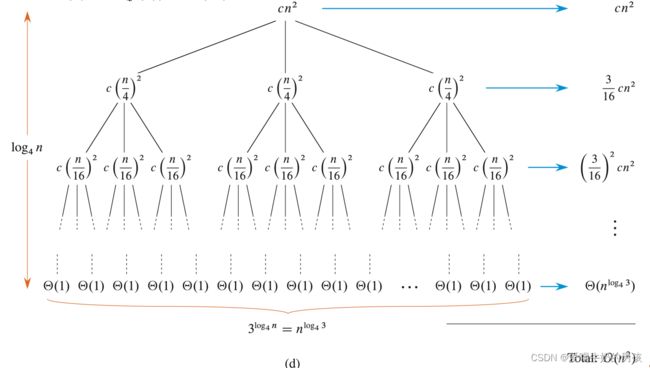
T ( n ) = 3 T ( n / 4 ) + Θ ( n 2 ) T(n) = 3T(n/4) + Θ(n^2) T(n)=3T(n/4)+Θ(n2)
最终递归树如图所示,每一层(除根节点)都和上一层差距 3 / 16 < 1 3/16 < 1 3/16<1 倍,因此 T ( n ) = O ( f ( n ) ) = O ( n 2 ) T(n) = O(f(n)) = O(n^2) T(n)=O(f(n))=O(n2)
但有的递归树各层节点值之和并不构成几何级数:
T ( n ) = 2 T ( n / 2 ) + n / l g n T(n) = 2T(n/2) + n/lg n T(n)=2T(n/2)+n/lgn
第 i i i 层的和为 n / l g ( n / 2 i ) = n / ( l g n − i ) n/lg(n/2^i) = n/(lg n − i) n/lg(n/2i)=n/(lgn−i), l g n − i ≥ 1 ⇒ i ≤ l g n − 1 lg n − i ≥ 1 ⇒ i ≤ lg n − 1 lgn−i≥1⇒i≤lgn−1
T ( n ) = ∑ i = 0 L n / ( l g n − i ) = ∑ i = 0 l g n − 1 n / ( l g n − i ) = = ∑ j = 1 l g n n / i T(n) = \sum_{i=0}^{L}n/(lg n − i) = \sum_{i=0}^{lgn - 1}n/(lg n − i) = = \sum_{j=1}^{lgn}n/ i T(n)=∑i=0Ln/(lgn−i)=∑i=0lgn−1n/(lgn−i)==∑j=1lgnn/i
使用调和级数: H n = ∑ i = 1 n 1 / i = Θ ( l o g n ) H_n = \sum_{i=1}^{n}1/i = Θ(log n) Hn=∑i=1n1/i=Θ(logn)
因此 T ( n ) = ∑ j = 1 l g n n / i = n H l g n = Θ ( n l g l g n ) T(n) = \sum_{j=1}^{lgn}n/ i = nH_{lgn} =Θ(n lg lg n) T(n)=∑j=1lgnn/i=nHlgn=Θ(nlglgn)
T ( n ) = 4 T ( n / 2 ) + n l g n T(n) = 4T(n/2) + n lg n T(n)=4T(n/2)+nlgn
第 i 层共有 4 i 4^i 4i 个节点,其每个节点的时间花销: ( n / 2 i ) l g ( n / 2 i ) = ( n / 2 i ) ( l g n − i ) (n/2^i)lg(n/2^i) = (n/2^i)(lgn - i) (n/2i)lg(n/2i)=(n/2i)(lgn−i)
因此总的时间花销: T ( n ) = ∑ i = 0 l g n ( n / 2 i ) ( l g n − i ) = Θ ( n 2 ) T(n) = \sum_{i=0}^{lgn}(n/2^i)(lgn - i) = Θ(n^2) T(n)=∑i=0lgn(n/2i)(lgn−i)=Θ(n2)
T ( n ) = n T ( n ) + n T(n) = n T( n) + n T(n)=nT(n)+n
前几层的节点时间花销之和:
T ( n ) = ∑ i = 0 L n T(n) = \sum_{i=0}^{L}n T(n)=∑i=0Ln, L = l g l g n L = lg lg n L=lglgn
T ( n ) = Θ ( n l g l g n ) T(n) = Θ(n lg lg n) T(n)=Θ(nlglgn)
T ( n ) = T ( n / 3 ) + T ( 2 n / 3 ) + n T(n) = T(n/3) + T(2n/3) + n T(n)=T(n/3)+T(2n/3)+n
该递归公式,最终绘制成的递归树,左右是不平衡的。
考虑上界和下界:
l o g 3 n ≤ L ≤ l o g 3 / 2 n log_3n ≤ L ≤ log_{3/2}n log3n≤L≤log3/2n
上界: T ( n ) ≤ ∑ i = 0 l o g 3 / 2 n i = n l o g 3 / 2 n T(n) ≤ \sum_{i=0}^{log_{3/2}n} i = nlog_{3/2}n T(n)≤∑i=0log3/2ni=nlog3/2n
上界: T ( n ) ≤ ∑ i = 0 l o g 3 n i = n l o g 3 n T(n) ≤ \sum_{i=0}^{log_{3}n} i = nlog_{3}n T(n)≤∑i=0log3ni=nlog3n
因此: T ( n ) = Θ ( n l o g n ) T(n) = Θ(n log n) T(n)=Θ(nlogn)