【数据结构 | 堆及其堆排序】
数据结构 | 堆及其堆排序
- 堆
-
- 堆的数据结构:
-
- 堆的插入
- 堆的删除
- 堆排
- Heap.c
堆
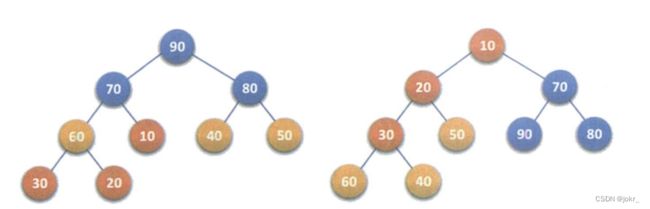
堆(Heap)是计算机科学中的一种数据结构,它是一种特殊的树形结构,并且,堆是具有如下性质的完全二叉树:
大顶堆:每个结点的值都大于或等于其左右孩子结点的值
第一个是大堆
第二个是小堆
堆的数据结构:
堆的插入
因为在物理结构上来看,堆是一个数组
而在逻辑上来看堆是一个完全二叉树
所以对于堆的插入即在数组的尾部插入数据。
void HeapPush(HP* php, HPDataType x)
{
assert(php);
if (php->capacity == php->size)
{
int newCapacity = php->capacity == 0 ? 4 : php->capacity * 2;
HPDataType* tmp = (HPDataType*)realloc(php->a, sizeof(HPDataType) * newCapacity);
if (tmp == NULL)
{
perror("realloc fail");
exit(-1);
}
php->a = tmp;
php->capacity = newCapacity;
}
php->a[php->size] = x;
php->size++;
AdjustUp(php->a, php->size - 1);
}
此处,因为每次都是在数组的尾部插入一个数字,所以每次都要对这个数字进行向上调整,这里我们以建立大堆为例子:
void AdjustUp(HPDataType* a, int child)
{
int parent = (child - 1) / 2;
while (child > 0)
{
if (a[child] > a[parent])
{
Swap(&a[child], &a[parent]);
child = parent;
parent = (parent - 1) / 2;
}
else
{
break;
}
}
}

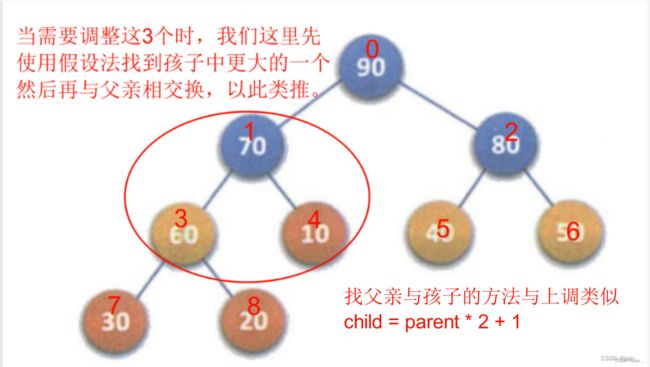
当孩子与其父亲比较时,孩子大于父亲则将二者想换,![]()
直到child != 0时,那么这时的堆才是大堆
那这个parent是怎么计算的呢?
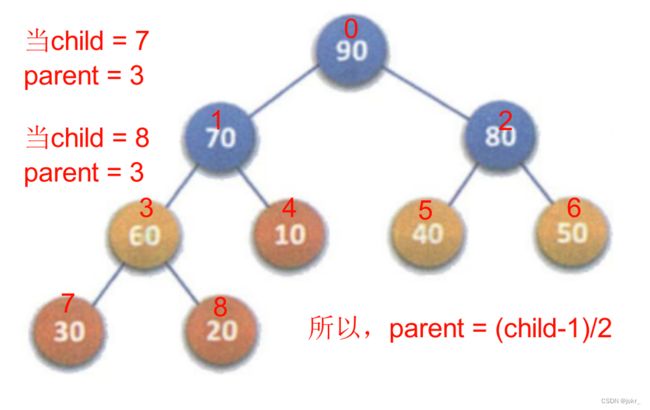
当child走到0时,即上调完成。
堆的删除
堆的删除,规定只能删除堆顶的元素,即将堆顶元素和最后一个元素相互交换,然后再下调。
//规定删除栈顶元素
void HeapPop(HP* php)
{
assert(php);
assert(php->size > 0);
Swap(&php->a[0], &php->a[php->size - 1]);
php->size--;
AdjustDown(php->a, php->size, 0);
}
同理,先Swap然后再向下调整
void AdjustDown(HPDataType* a, int size, int parent)
{
int child = parent * 2 + 1;
while (child < size)
{
if ((a[child] < a[child + 1]) && child + 1 < size)
{
child++;
}
if (a[parent] < a[child])
{
Swap(&a[child], &a[parent]);
parent = child;
child = child * 2 + 1;
}
else
{
break;
}
}
}
堆排
堆排序就是利用堆(假设利用大顶堆)进行排序的方法。它的基本思想是’将待
排序的序列构造成-个大顶堆°此时’整个序列的最大值就是堆顶的根结点。将它移走
(具实就星将具与堆数组的末尾元素交换,此时末尾元素就是最大值),然后将剩余的
门n-1个序列重新构造成一个堆,这样就会得到n个元素中的次大值。如此反复执行便能得到-个有序序列了。
void HeapSort(int* a, int n)
{
for (int i = (n - 1 - 1) / 2; i >= 0; i--)
{
AdjustDown(a, n, i);
}
int end = n - 1;
while (end > 0)
{
Swap(&a[0], &a[end]);
AdjustDown(a, end, 0);
end--;
}
}
在建堆的时候,我们先从最后一个有孩子的节点开始下调,这样排的效率高。
然后再交换,吧最后一个剔除,再进行。
类如排下面这个数组

这个是排的大堆:

将第一个和最后一个交换,
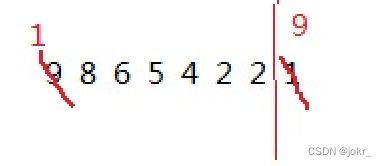
这个是此时的堆,进行下调:
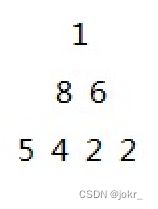
下排后:


Heap.c
#define _CRT_SECURE_NO_WARNINGS 1
#include"Heap.h"
//小堆
void HeapInit(HP* php)
{
assert(php);
php->a = NULL;
php->capacity = php->size = 0;
}
void HeapDestroy(HP* php)
{
assert(php);
free(php->a);
php->a = NULL;
php->capacity = php->size = 0;
}
void HeapPush(HP* php, HPDataType x)
{
assert(php);
if (php->capacity == php->size)
{
int newCapacity = php->capacity == 0 ? 4 : php->capacity * 2;
HPDataType* tmp = (HPDataType*)realloc(php->a, sizeof(HPDataType) * newCapacity);
if (tmp == NULL)
{
perror("realloc fail");
exit(-1);
}
php->a = tmp;
php->capacity = newCapacity;
}
php->a[php->size] = x;
php->size++;
AdjustUp(php->a, php->size - 1);
}
//规定删除栈顶元素
void HeapPop(HP* php)
{
assert(php);
assert(php->size > 0);
Swap(&php->a[0], &php->a[php->size - 1]);
php->size--;
AdjustDown(php->a, php->size, 0);
}
HPDataType HeapTop(HP* php)
{
assert(php);
assert(php->size > 0);
return php->a[0];
}
size_t HeapSize(HP* php)
{
assert(php);
return php->size;
}
bool HeapEmpty(HP* php)
{
assert(php);
return php->size == 0;
}
void Swap(HPDataType* p1, HPDataType* p2)
{
HPDataType tmp = *p1;
*p1 = *p2;
*p2 = tmp;
}
void AdjustUp(HPDataType* a, int child)
{
int parent = (child - 1) / 2;
while (child > 0)
{
if (a[child] > a[parent])
{
Swap(&a[child], &a[parent]);
child = parent;
parent = (parent - 1) / 2;
}
else
{
break;
}
}
}
void AdjustDown(HPDataType* a, int size, int parent)
{
int child = parent * 2 + 1;
while (child < size)
{
if ((a[child] < a[child + 1]) && child + 1 < size)
{
child++;
}
if (a[parent] < a[child])
{
Swap(&a[child], &a[parent]);
parent = child;
child = child * 2 + 1;
}
else
{
break;
}
}
}
void HeapSort(int* a, int n)
{
for (int i = (n - 1 - 1) / 2; i >= 0; i--)
{
AdjustDown(a, n, i);
}
int end = n - 1;
while (end > 0)
{
Swap(&a[0], &a[end]);
AdjustDown(a, end, 0);
end--;
}
}