《堆》的模拟实现
目录
前言:
模拟实现《堆》:
1.自定义数据类型
2.初始化“堆”
3.销毁“堆”
4.进“堆”
关于AdjustUp()
5.删除堆顶元素
关于AdjustDown()
6.判断“堆”是否为空
7.求“堆”中的数据个数
8.求“堆”顶元素
总结:
前言:
我们在上一篇的blog中对于《树》有了初步的认识,树的包含多种数据结构,其中我们现阶段最适合引入“堆”的概念,我们同时也在上一篇的blog中的最后引入并介绍了“堆”的相关概念,了解到了小堆以及大堆。具体内容可以参考上一篇blog:
初识《树》-CSDN博客
本次blog就以小堆为例,动手模拟开辟出一个“小堆”!
模拟实现《堆》:
1.自定义数据类型
typedef int HPDataType;
typedef struct Heap
{
HPDataType* a;
int size;
int capacity;
}HP;是的,本次堆的实现我们利用到了顺序表的存储概念,我们在后面会讲到为什么要使用顺序表。
2.初始化“堆”
void HeapInit(HP* php)
{
php->a = NULL;
php->capacity = php->size = 0;
}3.销毁“堆”
void HeapDestory(HP* php)
{
assert(php);
php->size = php->capacity = 0;
free(php->a);
}初始化和销毁这两个函数在我们之前的blog中有讲解,而且内容相差不大所以我们在这里不给予讲解,我也不再进行过多赘述。
4.进“堆”
void HeapPush(HP* php, HPDataType x)
{
assert(php);
int newcapacity = (php->capacity == 0) ? 4 : 2 * php->capacity;
HPDataType* tmp = (HPDataType*)realloc(php->a, sizeof(HPDataType)* newcapacity);
if (tmp == NULL)
{
perror("realloc error");
exit(-1);
}
php->a = tmp;
php->capacity = newcapacity;
php->a[php->size] = x;
AdjustUp(php->a, php->size);//向上调整建堆
php->size++;
}这里的开头也是与之前的顺序表一致,不同的地方在于我们创建了一个AdjustUp函数。
接下来我们就来讲解此函数:
关于AdjustUp()
void swap(int* a, int* b)
{
int tmp = *a;
*a = *b;
*b = tmp;
}
void AdjustUp(HPDataType* a, int child)
{
while (child > 0)
{
int parent = (child - 1) / 2;
if (a[parent] > a[child])
{
swap(&a[parent], &a[child]);
}
child = parent;
}
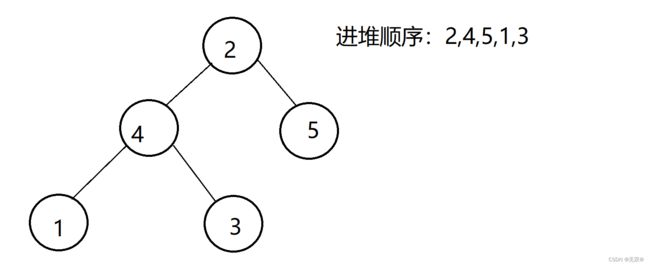
}我们先假设有一个数组,数组元素2,4,5,1,3
现在想要建小堆并让这些数据进“堆”,
还明显,该树并不是堆,既不满足小堆,更不满足堆!
所以我们需要进行调整,所以就有了向上调整法即AdjustUp()
具体的思路:
1.每插入一个数据,就于父亲节点相比较
2.如果父亲节点>孩子节点 那么数据进行交换,由于这是顺序表所以就是数组下标进行交换,同时注意我们在实现交换函数时,传递的是地址!
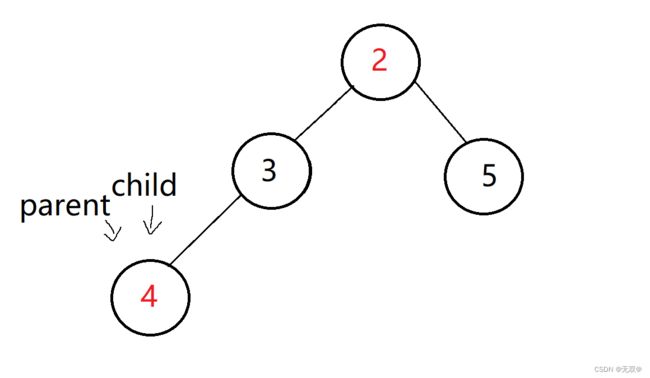
在此我用图来展示:
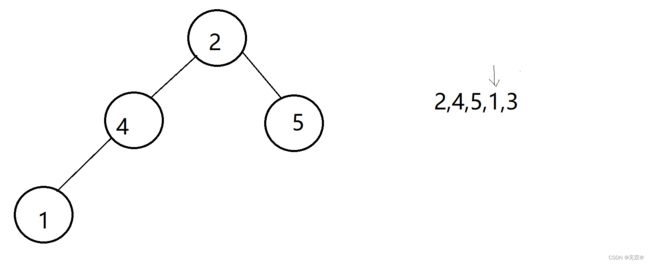
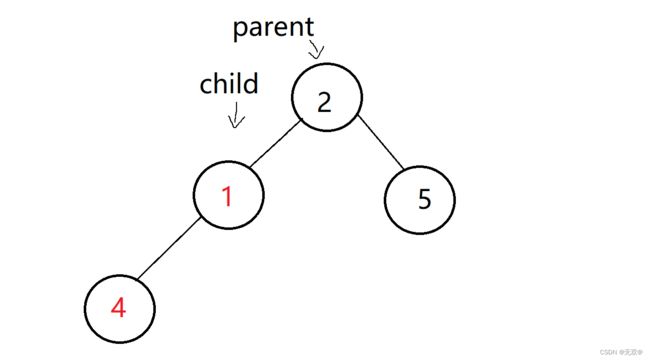
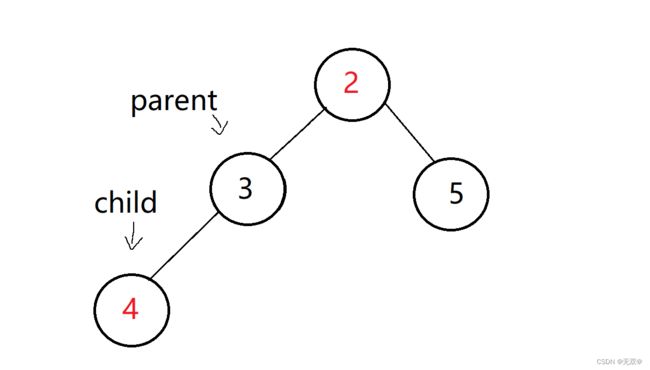
此时遍历到1这个小标,因为随着数据的添加,size也会++,所以数据1的下标就为size-1
那么我们就让size-1下标即数据1的位置座位child。
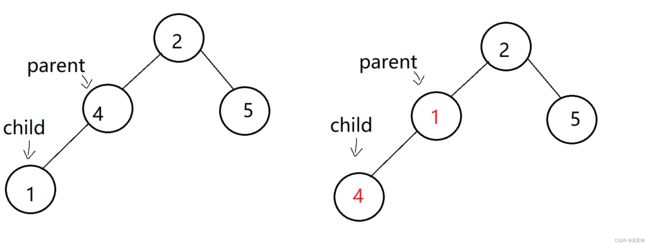
而我们想要找到数据1的父亲节点,不难得出公式
parent = (child - 1)/2
则可找到数据4作为父亲节点,然后进行交换,即:
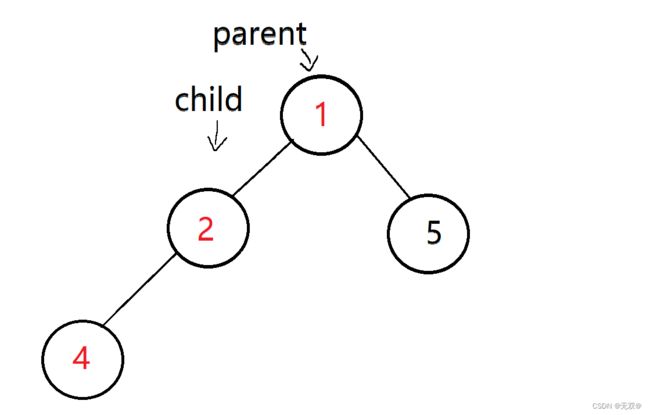
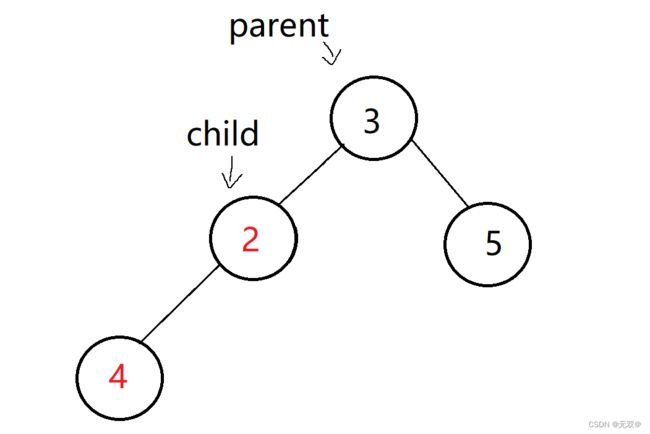
虽然交换完了数据1和数据4的节点,但是这还不是一个合格的堆,因此我们还要继续进行操作,这个时候我们的child就可以挪动到parent的位置即:
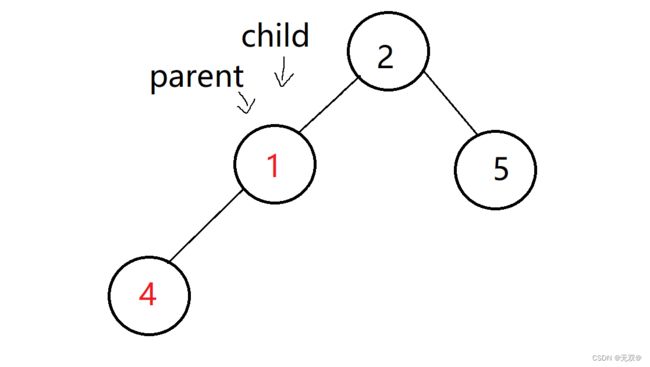
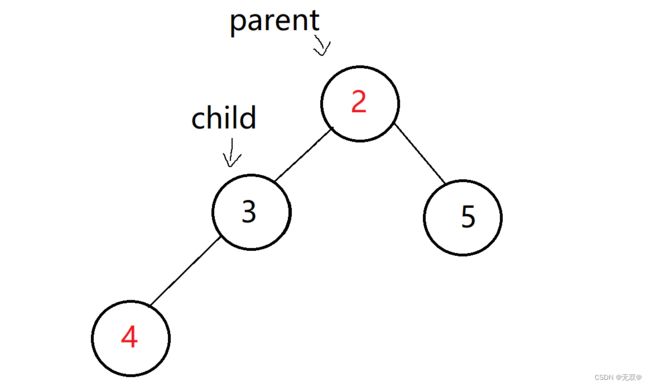
我们先要将数据1和数据2进行交换,交换完后才是一个小堆,所以这就是while循环在此的作用,而限制条件显而易见就是child不在首元素时状态。
所以parent = (child - 1) / 2
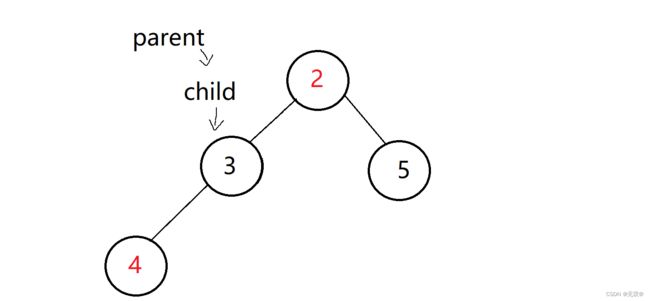
进行交换则有:
如此就是一个小堆了
5.删除堆顶元素
void HeapPop(HP* php)
{
assert(php);
//交换头尾元素
swap(&php->a[0], &php->a[php->size - 1]);
php->size--;
//向下调整
AdjustDown(php->a, php->size, 0);
}在我们熟悉进“堆”操作后,我们不妨来实现实现删除堆顶数据,具体的操作思路如下:
1.将首元素数据和最后一个数据交换。
2.再调整堆使其完善成小堆。
第一个步骤好理解,接下来我们就来介绍我们的第二个函数,AdjustDown()
关于AdjustDown()
void AdjustDown(HPDataType* a, int sz, int parent)
{
int child = 2 * parent + 1;
while (child < sz)
{
if (child + 1 < sz && a[child] > a[child + 1])
{
child++;
}
if (a[child] < a[parent])
{
swap(&a[child], &a[parent]);
parent = child;
}
else
{
break;
}
}
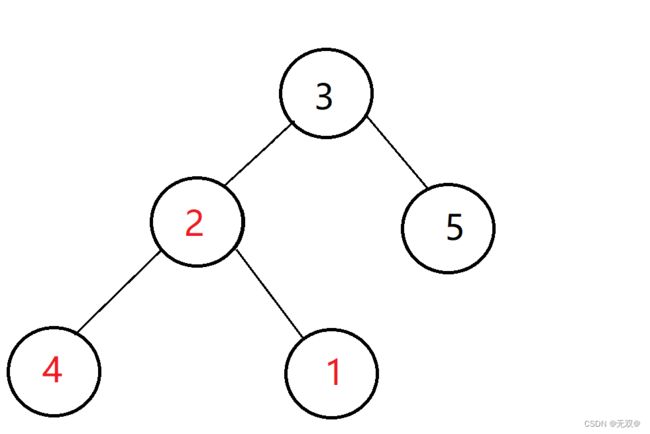
}先进行首尾互换,则有:
此时我们先让size--
目的是为了不管最后一个元素一,即:
可此时并不是一个合格的小堆,但是我们此时不能使用 向上调整法了,因为如果我们首元素一旦是一个很大的数,拿8举例,执行交换就是8和2进项交换,但是8仍然大于4,所以向上调整法不适用这里,因此我们可以得知向上调整法是适用于建堆!
那我们就要利用一种新的思路:
1.从首元素开始向下调整。
2.判断左孩子和右孩子的数哪个更小
3.取小的开始不断交换
我们在这里用图来说明:
我们在此是传递首元素,即父亲进来,那么我们可以通过公式
child = 2*parent + 1
找出左孩子的节点,然后进行判断:
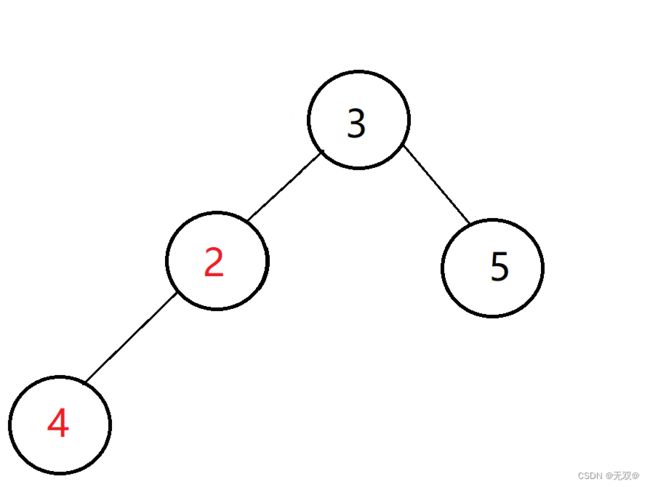
此时很明显左孩子小于右孩子所以进行判断
此时2<3所以进行交换
然后继续往下判断,parent = child;
继续通过公式有:
最后就有:
此时child还会继续找下一个数据,可是后续的数据就不是我们的数组内容了,因此交换的条件应当是child< size才能进行交换。
以上这两个函数就是本文的核心精华内容!
6.判断“堆”是否为空
bool HeapEmpty(HP* php)
{
assert(php);
if (php->size == php->capacity)
{
return true;
}
return false;
}7.求“堆”中的数据个数
int HeapSize(HP* php)
{
assert(php);
return php->size;
}8.求“堆”顶元素
int HeapTop(HP* php)
{
assert(php);
if (!HeapEmpty(php))
{
return php->a[0];
}
exit(-1);
}总结:
以上就是《堆》的模拟实现的全部内容,我们在实现AdjustUp函数和AdjustDown函数时不难发现,我们要经常找到上一个父亲节点的数据,所以我们才采取顺序表的结构来帮助我们查找。
下一篇的blog我们利用堆这一结构解决问题,包括《堆排序》,《Top-K》。
记住“坐而言不如起而行”
Action speak louder than words!
本文的代码在我的Gitee仓库:
Data structures amd algorithms: 关于数据结构和算法的代码 - Gitee.com